Исчисление конечных разностей [1] оперирует с конечными разностями числовой функции y=f(x), x,y∈R, и конечными разностями ее аргумента: b-a, a,b∈R, f(b)-f(a), f(a),f(b)∈R. Связь исчисления конечных разностей с дифференциальным исчислением [2] опирается на теорему Лагранжа о конечных приращениях (о промежуточной точке, о среднем значении), выражающую конечную разность функции через конечную разность аргумента с использованием значения производной этой функции в некоторой точке с, промежуточной между точками а и b:
![]() (1)
(1)
Наряду с конечными разностями b-a, f(b)-f(a) как аддитивными мерами различия чисел а и b, f(a) и f(b), в математике и ее приложениях используются конечные частные b/a, f(b)/f(a) - мультипликативные меры их различия.
Выражения конечных разностей/частных функции через конечные разности/частные аргумента, наряду с (1), могут быть получены из (1) путем логарифмирования/ экспоненцирования аргумента/функции:
![]() (2)
(2)
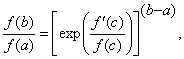 (3)
(3)
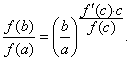 (4)
(4)
Исчисление конечных разностей и частных адекватно, среди прочих, современным задачам экономического факторного анализа [3].
СПИСОК ЛИТЕРАТУРЫ:
- Гельфонд А.О. Исчисление конечных разностей. - М.: Наука, 1967. - 432 с.
- Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. - СПб.: Лань, 1997. - 608 с.
- Блюмин С.Л., Суханов В.Ф., Чеботарев С.В. Экономический факторный анализ. - Липецк: ЛЭГИ, 2004. - 148 с.
Библиографическая ссылка
Блюмин С.Л. ИСЧИСЛЕНИЕ КОНЕЧНЫХ РАЗНОСТЕЙ И ЧАСТНЫХ // Фундаментальные исследования. 2008. № 3. С. 105-105;URL: https://fundamental-research.ru/ru/article/view?id=2814 (дата обращения: 02.02.2026).



