Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Файлы

Герасимов С.А.

Статья в формате PDF

338 KB

На рис. 1 изображена установка, предназначенная для достаточно простых и, одновременно, точных измерений силы аэродинамического сопротивления. Смысл проведения таких измерений в настоящее время стал достаточно актуален. В динамическом режиме сила аэродинамического сопротивления [1] существенно отличается от силы сопротивления, соответствующей неизменной скорости среды относительно тела [2]. Вращательное движение, являющееся частным случаем динамического режима, осталось неизученным. Едва ли достаточной является попытка измерить силу аэродинамического сопротивления, действующего на снабженный лопастями маятник Максвелла [3].

После выключения двигателя D, позволяющего достичь больших скоростей движения исследуемого тела B, угловая скорость со временем изменяется как

,                             (1)

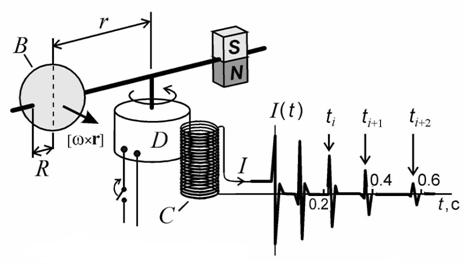
Рис. 1. Схема эксперимента

где ω₀ - угловая скорость вращения исследуемого тела в момент времени t=0, а коэффициенты торможения a связаны с моментами инерции подвижной нагруженной J и ненагруженной J_* исследуемым телом системы связаны с коэффициентом аэродинамического сопротивления C соотношением:

.                           (2)

С другой стороны, выражение (1) означает, что моменты времени t_i и t_i+1, при которых индукционный ток I(t), регистрируемый соленоидом C, максимален, удовлетворяют системе уравнений

,

имеющей нетривиальное аналитическое решение. А это, в свою очередь, допускает решение обратной задачи: восстановление зависимости коэффициента сопротивления от скорости тела в среде.

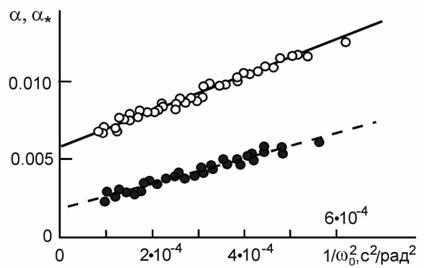
Рис. 2. Коэффициенты торможения для рабочего (○) и холостого (●) режимов

Для подвижной системы с параметрами J=8.2×10^-5кг×м², J_*=8.4×10^{-5 кг}×м², r=0.093м и сферы радиусом R=0.02м экспериментальные значения a и a_* представлены на рис. 2. Обращает внимание на себя характер зависимости коэффициентов торможения от угловой скорости вращения:

.

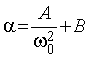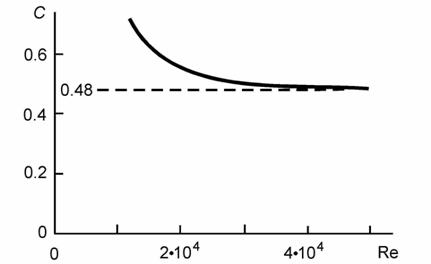
Рис. 3. Коэффициенты аэродинамического сопротивления (сплошная кривая) при различных числах Рейнольдса

Это дает возможность вычислить зависимость коэффициента аэродинамического сопротивления от числа Рейнольдса Re=rw₀r/m (m - вязкость воздуха). Результаты эксперимента (рис. 3) оказались достаточно противоречивыми. С одной стороны, при больших числах Рейнольдса экспериментальные результаты достаточно близки известным данным C=0.4, а это подтверждает возможность решения обратной задачи. С другой стороны, в области малых скоростей настоящие экспериментальные данные существенно завышены. Этот результат является чрезвычайно важным при создании летательного аппарата с вращающимися крыльями [4].

СПИСОК ЛИТЕРАТУРЫ:

1. Герасимов С.А. Об автомодельности аэродинамического сопротивления. // Вестник машиностроения. 2007. № 1. С. 34-35.
2. Sovran G., Morel T., Mason W.T. Aerodynamic Drag Mechanisms of Bluff Bodies and Road Vehicles. - New York: Plenum Press, 1978. - 360 p.
3. Благодарный В.В. Маятник Максвелла в опытах по аэродинамике. // Учебная физика. 2007. № 1. С. 103-106.
4. Герасимов С.А. Экранолет +. // Авиация общего назначения. 2007. № 8. С. 10-12.

Библиографическая ссылка