Для выбора оптимальных условий сушки зернового материала в устройствах, использующих проволочные винты, необходимо знать распределение температуры в зерновом слое. Рассмотрим слой толщиной 
. Если толщина мала по сравнению с длиной и шириной, то можно считать его неограниченным.
При заданных граничных условиях, когда температура точек поверхностей справа и слева задана. Изменение температуры происходит только в одном направлении х, в двух других направлениях температура не изменяется 
, следовательно, в пространстве задача является одномерной. Начальное распределение температуры задано 
. Нагревание происходит за счет разности температур.
Так как задача в пространстве одномерная, то дифференциальное уравнение принимает вид:
(1)
Начальные условия:
при 
. (2)
Граничные условия:
при 
(3)
Дифференциальное уравнение совместно с начальными и граничными условиями однозначно формулируют поставленную задачу.
Окончательно решение уравнения (1) запишется
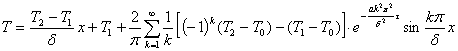(4)
При больших значениях 
уже при 
мин распределение температуры будет почти линейным.
. (5)
Так же получено решение при граничных условиях второго рода:
(6)
Библиографическая ссылка
Исаев Ю.М., Гришин О.П., Настин А.А. НЕСТАЦИОНАРНЫЙ ПРОГРЕВ ЗЕРНОВОГО СЛОЯ // Фундаментальные исследования. – 2008. – № 3. – С. 64-64;URL: https://fundamental-research.ru/ru/article/view?id=2777 (дата обращения: 20.09.2024).