Приводятся результаты исследования систем управления одним из распространенных классов технологических процессов, принцип работы которых основан на смеси двух или более физических принципов, имеющих существенные различия в инерционности. Методы построения управляющих систем такими процессами развиваются на кафедре «Автоматизированные системы обработки информации и управления».
Главная идея построения управляющих систем для процессов такого класса (называемых разнотемповыми) состоит в разделении задачи управления на несколько уровней, функционирование которых происходит в разных масштабах времени. Соответствующий подход рассматривается далее применительно к процессам с двумя разнотемповыми составляющими:
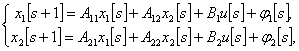
где x1[s] и x2[s] - векторы состояния объекта, соответствующие медленному и быстрому субпроцессам, u[s] - вектор управляющих воздействий, φ1[s], φ2[s] - векторы размерности n1х1 и n2х1, определяются по формулам:
φ1[s] = A12(E - A22)-1F2[s] + F1[s],
φ2[s] = (E - A22)-1F2[s],F1[s] и F2[s] - векторы детерминированных возмущающих воздействий, Аij, i, j = 1, 2 и Bi, i = 1, 2 - параметры дискретных моделей объекта, n1 + n2 = n - общий порядок модели объекта.
При этом управляющая система строится как двухуровневая, форма ее реализации - цифровая. Согласно принятой терминологии такие системы называются управляющими системами с двойной шкалой времени (далее - ДШВ).
Верхний уровень управляющей системы ответственен за управление медленной динамикой.
Нижний уровень ответствен за подавление собственной динамики быстрого субпроцесса, вызываемой изменениями начальных условий в моменты резких изменений задающих воздействий.
Управляющее воздействие строится как составное. Его составляющими являются:
- медленное управление, рассчитываемое с дискретой Δt, выбор которой определяется свойствами динамики медленной составляющей процесса. Основа выбора - теорема Котельникова и ее инженерные приложения;
- быстрое управление, рассчитываемое с существенно меньшей дискретой t. Выбор быстрой дискреты осуществляется на основе рекомендаций теории систем с ДШВ на основании определения продолжительности пограничного слоя, в течение которого заметно влияние свободной динамики быстрого субпроцесса.
Предметом исследования является совокупность вопросов, недостаточно отраженных в предшествующих результатах и потому требующих специального изучения. Этот комплекс вопросов относится к взаимодействию между быстрой и медленной подсистемами, и к оценке эффективности составного управления.
Методика исследования построена по следующей схеме. Для того, чтобы исключить влияние субъективных факторов на выбор стратегии управления используется постановка задачи управления в оптимизационных терминах согласно теории аналитического конструирования оптимальных регуляторов (АКОР).
Процесс генерации моделей для управляющих контуров разного уровня производится с использованием формулы Лагранжа-Сильвестра.
Для последующих вычислительных экспериментов были предложены специальные формулы, генерирующие модель объекта с наличием двух разнотемповых субпроцессов. Генерация дискретных моделей для каждого из уровней управляющей системы производится из условия совпадения значения векторов состояния исходной непрерывной и порождаемых моделей в точках отсчета дискрет времени.
Эталонное качество управления рассчитывается по результату решения АКОР-задачи на модели объекта в быстром масштабе времени без декомпозиции динамики процесса на субпроцессы.
Далее производятся исследования различных вариантов законов субоптимального управления. Источники упрощения - двух типов. Первый состоит в отказе выдачи управляющего воздействия АКОР-алгоритма в каждом такте быстрого времени. Вариации этого приема: либо рассчитывать управляющие воздействия, постоянные на интервале дискретизации медленного времени на верхнем уровне управляющей системы и передавать ее на нижний уровень для непосредственного применения, либо рассчитывать на верхнем уровне параметры этого алгоритма, постоянные для всей текущей дискреты медленного времени, и затем передавать их на нижний уровень для самостоятельного формирования управляющего воздействия.
Данный вариант не использует идеи ДШВ, но является источником для оценки: будет ли улучшен критерий работы системы, если идеи ДШВ использовать. Второй вариант упрощения состоит в прямом использовании идеи ДШВ. При этом сложность задач управления для каждого из уровней УС понижается до размерности субпроцессов. Вариации этого приема: использовать только медленное управление (как это было в монографии), либо использовать составное управление, примеры по которому в монографии не были рассчитаны.
Сопоставимость результатов вычислительных экспериментов обеспечивается тем, что критерий качества работы системы оценивается непосредственно по показателям в быстром времени.
В работе были получены результаты, обладающие признаками новизны:
- проведен синтез алгоритма для нижнего уровня УС, работающей в быстрой шкале времени;
- проведена серия вычислительных экспериментов, в которых УС генерирует составные управляющие воздействия;
- в результате экспериментов была подтверждена высокая эффективность введения составного управления по сравнению только с медленным управлением. В проведенной серии экспериментов достигнуто улучшения критерия оптимальности примерно на 85%;
- выявлена вспомогательная оптимизационная задача, настройки параметров для части критерия управления свободной составляющей быстрого субпроцесса.
Библиографическая ссылка
Соколов Д.С. ИССЛЕДОВАНИЯ ЭФФЕКТИВНОСТИ ОПТИМИЗАЦИОННЫХ АЛГОРИТМОВ В ЦИФРОВЫХ УПРАВЛЯЮЩИХ СИСТЕМАХ С ДВОЙНОЙ ШКАЛОЙ ВРЕМЕНИ // Фундаментальные исследования. 2008. № 1. С. 79-80;URL: https://fundamental-research.ru/ru/article/view?id=2396 (дата обращения: 12.03.2026).



