 , образованного наклонной плоскостью с горизонтом. Чем меньше угол наклона, тем больше совершаемая работа, т.к. работа пропорциональна квадрату импульса силы. При наличии трения в случае самопроизвольного скольжения (коэффициент трения
, образованного наклонной плоскостью с горизонтом. Чем меньше угол наклона, тем больше совершаемая работа, т.к. работа пропорциональна квадрату импульса силы. При наличии трения в случае самопроизвольного скольжения (коэффициент трения  ) работа силы тяжести возрастает при увеличении
) работа силы тяжести возрастает при увеличении  .
.
В курсах физики [1] определена работа силы тяжести, которую она совершает при переходе материальной точки из положения 1 в положение 2 вдоль прямолинейного отрезка 12 (рис. 1). Примером может служить скольжение без трения материальной точки по гладкой наклонной поверхности. Работа силы тяжести
![]() или
или ![]() (1)
(1)
где ![]() и
и ![]() – высоты, на которых находилась материальная точка в начале и конце пути, отсчитанные от какого-либо произвольного уровня, например, от земной поверхности или от уровня моря. Формула (1) остается справедливой и при перемещении вдоль произвольной кривой. Из этого делается вывод, что работа силы тяжести не зависит от формы пути и определяется только начальным и конечным положениями перемещающейся материальной точки. Силы, работа которых не зависят от формы траектории, называются потенциальными (консервативными). Если одно из положений материальной точки принять за нулевое, то работа, совершаемая консервативными силами при переходе системы из рассматриваемого положения в нулевое, определяет потенциальную энергию
– высоты, на которых находилась материальная точка в начале и конце пути, отсчитанные от какого-либо произвольного уровня, например, от земной поверхности или от уровня моря. Формула (1) остается справедливой и при перемещении вдоль произвольной кривой. Из этого делается вывод, что работа силы тяжести не зависит от формы пути и определяется только начальным и конечным положениями перемещающейся материальной точки. Силы, работа которых не зависят от формы траектории, называются потенциальными (консервативными). Если одно из положений материальной точки принять за нулевое, то работа, совершаемая консервативными силами при переходе системы из рассматриваемого положения в нулевое, определяет потенциальную энергию
![]() или
или ![]() (2)
(2)
Соотношение (2) является одним из основных заблуждений классической механики. В самом деле, потенциальная энергия – это энергия статического состояния, а работа может совершаться по разным траекториям и на ее совершение может затрачиваться различное время, т.е. импульс силы может иметь разные значения. В работах [2-4] показано, что в общем случае работа, совершаемая силой (производство энергии), пропорциональна квадрату импульса силы
![]() , где
, где ![]() (3)
(3)
И только в частном случае для результирующей силы ![]() , вызывающей ускоренное (или замедленное) движение тела в соответствии со вторым законом Ньютона
, вызывающей ускоренное (или замедленное) движение тела в соответствии со вторым законом Ньютона ![]() , работа может быть определена общепринятой формулой:
, работа может быть определена общепринятой формулой:
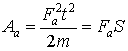 , т.к.
, т.к. ![]()
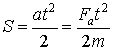 (4)
(4)
Для других сил работа должна определяться только по формуле (3). Выражение (1) определяет работу только одной составляющей силы тяжести
![]() , откуда
, откуда ![]() ;
; ![]() – время скольжения,
– время скольжения, ![]() - конечная скорость, равная конечной скорости при свободном падении тела.
- конечная скорость, равная конечной скорости при свободном падении тела.
Работа второй составляющей силы тяжести ![]() считается равной нулю на основании того, что она перпендикулярна плоскости скольжения, а
считается равной нулю на основании того, что она перпендикулярна плоскости скольжения, а ![]() . На самом же деле, если сила действует на тело, то «работают» все составляющие силы, «неработающих» сил не бывает. Если тело находится на опоре (рис. 2в), то деформировано (причем неравномерно по высоте) от действия нормальной реакции опоры, а сама опора (наклонная плоскость) деформирована в области места контакта от действия силы
. На самом же деле, если сила действует на тело, то «работают» все составляющие силы, «неработающих» сил не бывает. Если тело находится на опоре (рис. 2в), то деформировано (причем неравномерно по высоте) от действия нормальной реакции опоры, а сама опора (наклонная плоскость) деформирована в области места контакта от действия силы ![]() . По мере скольжения тела вниз, смещается вниз и место деформации. Работа, совершаемая силой
. По мере скольжения тела вниз, смещается вниз и место деформации. Работа, совершаемая силой ![]() :
:
![]() (5)
(5)
Поскольку силы ![]() и
и ![]() ортогональны, то работы этих сил аддитивны, т.е. складываются арифметически. Тогда суммарная работа тяжести будет равна
ортогональны, то работы этих сил аддитивны, т.е. складываются арифметически. Тогда суммарная работа тяжести будет равна
![]() (6)
(6)
или
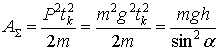 (7)
(7)
Зависимость суммарной работы ![]() в долях потенциальной работы
в долях потенциальной работы ![]() от угла наклона плоскости
от угла наклона плоскости ![]() дана на графике (рис. 3). Из графика следует, что чем меньше угол
дана на графике (рис. 3). Из графика следует, что чем меньше угол ![]() , тем больше работа
, тем больше работа ![]() , совершаемая силой тяжести, только при углах, близких к
, совершаемая силой тяжести, только при углах, близких к ![]() (вертикаль)
(вертикаль) ![]() .
.
Во что превращается работа силы ![]() ? При смещении места контакта вниз, ранее упруго деформированная часть опоры начинает совершать упругие колебания, которые быстро затухают вследствие дисперсии и внутреннего трения, переходя во внутреннюю энергию (происходит нагрев поверхности контакта). Таким образом, соотношение (6) можно представить в виде первого закона термодинамики
? При смещении места контакта вниз, ранее упруго деформированная часть опоры начинает совершать упругие колебания, которые быстро затухают вследствие дисперсии и внутреннего трения, переходя во внутреннюю энергию (происходит нагрев поверхности контакта). Таким образом, соотношение (6) можно представить в виде первого закона термодинамики
![]() (8)
(8)
где ![]() – производство энергии импульсом силы тяжести,
– производство энергии импульсом силы тяжести, ![]() - работа импульса силы
- работа импульса силы ![]() ,
, ![]() - изменение внутренней энергии за счет действия импульса силы
- изменение внутренней энергии за счет действия импульса силы ![]() .
.
Если наклонная плоскость шероховата, то движение происходит с некоторым коэффициентом трения ![]() . Будем рассматривать случай самопроизвольного скольжения тела (
. Будем рассматривать случай самопроизвольного скольжения тела (![]() ). В этом случае равноускоренное скольжение вниз будет происходить под действием силы
). В этом случае равноускоренное скольжение вниз будет происходить под действием силы ![]() . Время скольжения
. Время скольжения
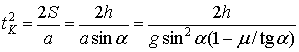 (9)
(9)
Работа, совершаемая силой тяжести, при скольжении с трением по наклонной поверхности
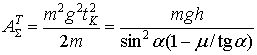 (10)
(10)
При коэффициенте трения ![]() получаем соотношение (7). На графике (рис.4.) показана зависимость отношения работы
получаем соотношение (7). На графике (рис.4.) показана зависимость отношения работы ![]() к работе силы тяжести
к работе силы тяжести ![]() при отсутствии трения в зависимости от отношения
при отсутствии трения в зависимости от отношения ![]() . Эти же величины приведены в таблице 1.
. Эти же величины приведены в таблице 1.
Таблица 1.
| | 0 | 0,2 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 0,95 |
| | 1 | 1,25 | 1,667 | 2 | 2,5 | 3,33 | 5 | 10 | 20 |
Скорость тела в конце наклонной плоскости:
![]() (11)
(11)
СПИСОК ЛИТЕРАТУРЫ:.
1.Сивухин Д.В. Общий курс физики. Том 1. Механика. – М.: Наука, 1989.
2.Иванов Е.М. Работа и энергия в классической механике и I закон термо-динамики // Фундаментальные исследова-ния, №8, 2005, с.11.
3.Иванов Е.М. Работа при движении тел с трением // Фундаментальные исследования, №6, 2005, с.10.
4.Иванов Е.М. Определение работы и работа силы трения // Успехи современного естествознания, №8, 2005, с.10.
Библиографическая ссылка
Иванов Е.М. РАБОТА СИЛЫ ТЯЖЕСТИ ПРИ СКОЛЬЖЕНИИ ТЕЛА ПО НАКЛОННОЙ ПЛОСКОСТИ // Фундаментальные исследования. 2007. № 1. С. 13-15;URL: https://fundamental-research.ru/ru/article/view?id=2248 (дата обращения: 28.02.2026).



