Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Файлы

Святсков В.А.

Статья в формате PDF

138 KB

I. ВВЕДЕНИЕ

1. Основные сведения.

В основу этого исследования положена работа автора [1]. Следуя обозначениям этой работы, рассмотрим следующую задачу:

 (I.2)

В начальной задаче (I.1), (I.2) введены следующие обозначения: 

σ ≥ 0 - некоторый заданный параметр;

x – независимая переменная функции y=y(x),

 - некоторые заданные полиномы степени не выше третьей от своих аргументов со следующим свойством: при x = 0

      (I.3)

полином b(x) в общем случае

                 (I.4)

2. Некоторые основные свойства начальной задачи.

При  из уравнения (I.1) получим

 .       (I.5)

Из формул (I.1), (I.5) следует, что уравнение (I.5) является по своей сути предельным уравнением для уравнения (I.1).

Начальная задача (I.5), (I.2) может иметь особую точку в своем решении y=y(x). Это связано с нулевыми ограничениями (I.2), (I.3) и условием (I.4). Чтобы удовлетворить выражению (I.4) для решения y=y(x) должно выполняться условие

          (I.6)

что означает

при                         (I.7)

Если в задаче (I.1), (I.2) σ малый параметр, то эта задача имеет характер сингулярно возмущенной со следующим свойством: при малом параметре σ = 0 , порядок уравнения (I.1) не понижается, само уравнение (I.5) приобретает особую точку. Такой класс уравнений ввел в рассмотрение С.А. Ломов и сейчас активно исследуется его учениками.

3.  Обобщенный степенной ряд.
Формально определим обобщенный степенной ряд (ряд Пюизё)

           (I.8)

В некоторых задачах из [1]:

          (I.9)

II. ВЫВОДЫ И СХЕМА ИССЛЕДОВАНИЯ

1.   Решения многих прикладных задач можно получить из начальной задачи (I.5), (I.2) уравнения Эйлера - Лагранжа в качестве экстремалей.

2.   Эти решения в явном виде имеют вид обобщенного степенного ряда (I.9).

3.   Эти решения имеют особую точку в начальной точке со свойством (I.7).

4.   В силу свойства (I.7) получить аналитические решения на основе систем аналитических вычислений таких, как Maple, MathCad, в действительной области практически невозможно.

5.   Стандартные численные методы (Рунге Кутта и т.д.) и процедуры (RKF45 и т.д.) для решения задачи Коши в окрестности особой точки не применимы

6.    Предложенный автором метод можно использовать при численном решении подобных задач в качестве разгона.

Пусть приняты обозначения 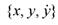  и заданы начальные условия (I.2).  При   строим решение вида (I.8).

Из формулы (I.8) получим

7.    Конечные значения (II.1) можно использовать в качестве начальных условий численного решения задачи Коши для уравнения (I.5).

III. ВВЕДЕНИЕ ПОГРАНИЧНОГО СЛОЯ

1). Определение (Математическая энцикло едия, m.V)

Пограничного слоя теория - асимптотическое приближение решения граничных задач для дифференциальных уравнений с малым параметром при старших производных (сингулярных за дач) в подобластях с существенным влиянием членов со старшими производными на решение.

2). Применение.

Уравнение (I.1) - ОДУ второго порядка является существенно нелинейным. Из него нельзя получить, как частный случай, линейное даже при определенном подборе параметров. Существование особой точки связано с нарушением усиленного условия Лежандра. В зависимости от значения параметра σ возможно существование следующих типов задач.

1.  При конечном значении σ>0 это уравнение поддается исследованию классическими методами (аналитическими, численными и т. д.).

2.  Автором   подробно   исследован   случай  Задача Коши (I.5), (I.2) и ее решение имеют особую точку.

3.  При это уравнение имеет характер сингулярно возмущенного со следующим свойством: при малом параметре равном нулю порядок уравнения не понижается, само уравнение становится с особой точкой.

Из процесса исследования автором затрону той проблемы можно сделать следующий вывод: окрестность особой точки формирует математический пограничный слой. В этом пограничном слое решение задач Коши приможет быть представлено в виде ряда Пюизё (I.8).

IV. ПРИЛОЖЕНИЯ

Все исследования автора по затронутой теме можно классифицировать следующим образом.

1. Математика.

1.1. Непрерывность.

1. Вариационное исчисление.

2. Связь с теорией сингулярно возмущенных задач.

3. Плоские кривые с точкой возврата (брахи стохрона, парабола Нейля и т.д.).

1.2 Дискретность.

1. Гомоморфизм.

2. Структура алгебры элементов уравнения Эйлера-Лагранжа.

3. Групповой анализ.

2. Прикладная механика.

2.1. Теоретическая механика.

1. Прямолинейное движение тела перемен ной массы.

2. Теорема об изменении кинетического мо мента механической системы с переменным мо ментом инерции.

2.2. Техника.

1. Определение оптимальной формы тела в гиперзвуковом невязком потоке.

2. Движение тела переменной массы в случае нулевых начальных условий.

3. Вращательное движение твердого тела с переменным моментом инерции.

СПИСОК ЛИТЕРАТУРЫ:

1. Святсков В. А. Уравнение Эйлера - Лагран-жа в пограничном слое и его приложения: моно графия.  2-е изд., исправ.  - Чебоксары:  ЧПИ МГОУ, 2008. - 135 с.

Библиографическая ссылка