Рассмотрим процессы, происходящие в непрерывном материальном сходящемся (расходящемся) потоке. Место, куда сходятся частицы потока и откуда они затем снова расходятся, назовем ядром потока. Выделим в потоке на расстоянии r от ядра частицу с бесконечно малыми размерами и бесконечно малым углом схождения dφ. Из математики известно, что бесконечно малая дуга и стягивающая ее хорда эквивалентны. Поэтому, заменив дуги стягивающими их хордами, мы получим частицу потока в форме правильной усеченной пирамиды ABCDEFGH .
Продольные размеры частицы равны:
AD= BC = EH = FG= dr
где dr – бесконечно малая величина. Поперечные размеры частицы равны:
AB = BF = EF = AE = (r + dr ) dϕ
CD = CG = GH = DH = rd ϕ
Объем частицы составит:Vч,r = r 2 dr dϕ 2
A1B1 = B1F1 = E1F1 = A1E1 = dr d ϕ
Так как высота этой пирамиды равна dr, то объем частицы составит:
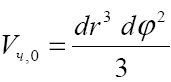
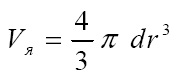
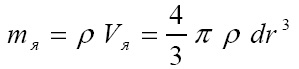
Тогда масса частицы равна:
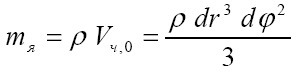
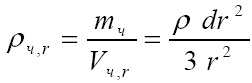
Это -бесконечно малая величина второго порядка, и, имея такую плотность, частица свободно проходит через ядра других потоков.
Продольный размер частицы равен dr. Так как поток является непрерывным, то расстояние dr есть путь, который частица проходит в сторону ядра за бесконечно малое время dt. Мы рассматриваем простейший случай, когда частица движется с постоянной скоростью c, т.е. dr = c dt . Важной особенностью непрерывного потока является то, что если частица движется с ускорением d2r/dt2 , то она деформируется в продольном направлении на величину d2r за время dt, причем:
а) если скорость частицы увеличивается, то частица растягивается;
б) если скорость частицы уменьшается, то частица сжимается.
При движении частицы к ядру, ее поперечный размер деформируется (сжимается) на величину dr dφ за время dt. Так как угол BAD у основания частицы равен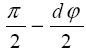 
а не строго , 
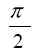то эта деформация проецируется на продольный размер частицы. Эта проекция составляет 
.
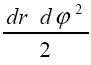Таким образом, в продольном направлении частица деформируется (сжимается) за время dt на величину 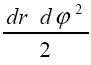. Следовательно, частица движется с бесконечно малым ускорением, которое направлено от ядра и равно:
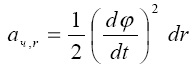
Пройдя через ядро, частица продолжает свое движение с той же скоростью, но уже от ядра. При этом ее поперечный размер растягивается. Эта деформация проецируется на продольный размер, что является причиной бесконечно малого ускорения частицы. Как и в случае движения частицы к ядру, это ускорение направлено от ядра.
Назовем удельной силу, действующую на единицу объема тела. Тогда удельная сила есть произведение плотности тела на его ускорение. На расстоянии r от ядра на частицу действует удельная сила, направленная от ядра и равная:
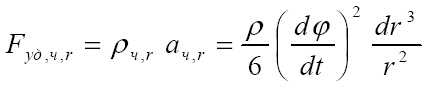
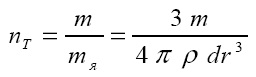
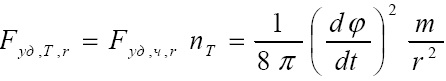
Материальная среда, окружающая тело Т, имеет постоянную конечную плотность ρMC. Эта среда состоит из частиц потоков всех тел во Вселенной. Очевидно, что удельная сила, противодействующая удельной силе Fуд,T,r, приложена к частице этой материальной среды и направлена в противоположную сторону, т.е. к телу Т. Тогда ускорение частицы материальной среды также направлено к телу Т и равно:
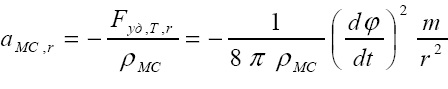
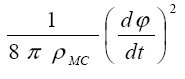постоянна. Обозначив ее как γ, получим: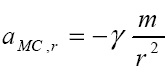
Библиографическая ссылка
Окунев И.В. ПРОЦЕССЫ В НЕПРЕРЫВНОМ ПОТОКЕ // Фундаментальные исследования. – 2009. – № 5. – С. 18-19;URL: https://fundamental-research.ru/ru/article/view?id=1644 (дата обращения: 03.12.2024).