В работе аналитическими и численными методами изучается физический процесс образования пленки в результате газовой или жидкостной эпитаксии на кристаллическую подложку.
Совокупность частиц неупорядоченной фазы можно рассматривать как ансамбль бозе-частиц. При температурах ниже некоторой критической происходит осаждение части частиц системы на подложку в состоянии с нулевым импульсом, так называемая бозе-конденсация в поле псевдопотенциала подложки. В результате на кристаллической поверхности образуются зародыши новой фазы, происходит фазовый переход первого рода [1, 2].
Предложена динамическая модель квазидвумерных решеток, в которой учтены решеточные ангармонизмы и ангармоническое взаимодействие плёнки с подложкой. Гамильтониан системы представлен в виде суммы одночастичного потенциала поля подложки и потенциала двухчастичного взаимодействия атомов плёнки с атомами подложки. Это дает возможность описывать «метастабильные» положения атомов в «метастабильных» локальных минимумах одного из потенциалов, а значит описывать метастабильные состояния решетки, связанные со структурно-фазовым переходом первого рода, близкого ко второму.
Несохранение числа частиц неупорядоченной системы, связанное с наличием поля подложки, приводит к появлению отличных от нуля средних 
, определяющих концентрацию частиц в газовой фазе, а также аномальных средних 
которые при k=0 определяют концентрацию осаждённых частиц - конденсата. Для аномальной функции Грина (ФГ):
получено уравнение:
,
где
.
Здесь ε - энергия одночастичных возбуждений.
Решая совместно систему уравнений для нормальной:
и аномальной ФГ находим для энергетической щели в спектре аномальной ФГ уравнение:
.
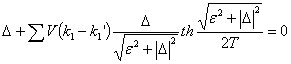Δ имеет смысл энергетической щели в спектре возбуждений монослоя кристаллического конденсата на подложке. Появление Δ≠0 является критерием начала конденсации несоразмерной фазы на кристаллической подложке.
Численное решение уравнения для энергетической щели Δ было проведено с помощью пакета MathCAD.
Экспериментальное подтверждение полученных результатов затруднено из-за сложности определения критических параметров в момент появления зародышей новой фазы. Но если отождествить ширину щели Δ с величиной активационного барьера адсорбционно-десорбционных процессов, то с помощью уравнения для энергетической щели Δ можно проследить зависимость энергии активации от степени покрытия.
Следует отметить, что формирование субмонослойных плёнок носит доменный характер, структура доменов зависит от величины покрытия, и эта зависимость носит пороговый характер.
Такой вывод позволяет предположить, что во всём интервале Δ xi, в пределах которого энергия активации меняется монотонно, латеральное взаимодействие между частицами плёнки оказывается неизменным, а некоторое изменение энергии активации в пределах интервала Δ xi связано с влиянием поля подложки. Скачкообразное же изменение энергии активации, свидетельствующее о структурных изменениях в плёнке, связано со скачкообразным изменением энергии двухчастичного взаимодействия. С учётом этого факта можно построить зависимость энергии активации от параметров двухчастичного взаимодействия и поля подложки (см. рис. 1).
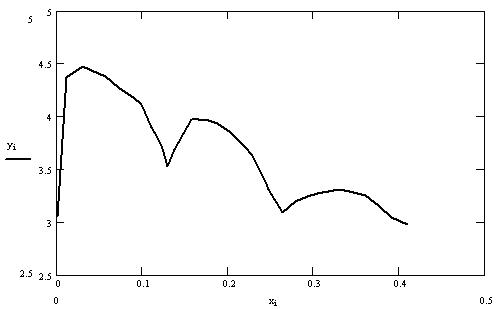
Рисунок 1. Зависимость энергии активации десорбции от степени покрытия
Сравнение полученного результата с экспериментальным [4] показывает, что для расчетной кривой в пределах одного монотонного участка изменение энергии активации коррелирует с изменением среднего поля подложки.
СПИСОК ЛИТЕРАТУРЫ
- Кукушкин С.А., Осипов А.В. Процессы конденсации тонких пленок. УФН, 1998, 168, 10, с.1083-1116.
- Децик В.Н., Каптелов Е.Ю. Кукушкин С.А., Осипов А.В., Пронин И.П. Кинетика начальной стадии фазового перехода первого рода в тонких пленках ФТТ, 1997, т.39, №1, с.121-126.
- Адхамов А.А., Лебедев В.И. Применение метода функций Грина в классической статистической механике. - Душанбе.: «Дониш», 1975. - 196 с.
- Крачино Т.В., Кузьмин М.В., Логинов М.В., Митцев М.А. Начальные стадии формирования границы раздела Yb-Si(III) ФТТ, 1997,т.39, №2, с.256-263. 33.20. Kf; 21.10.-k