Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Никитина А.В. 1 Семенякина А.А 1 Чистяков А.Е. 1 Проценко Е.А. 2 Яковенко И.В. 2

---

1 Научно-исследовательский институт многопроцессорных вычислительных систем имени академика А.В. Каляева, ГОУ ВО «Южный федеральный университет»

2 Таганрогский институт имени А.П. Чехова (филиал) ФГБОУ ВО «Ростовский государственный экономический университет (РИНХ)»

Работа посвящена применению схем повышенного порядка точности для решения задач биологической кинетики. Для решения поставленной задачи были построены и изучены дискретные аналоги операторов конвективного и диффузионного переносов четвертого порядка точности в случае частичной заполненности ячеек. Были проведены численные эксперименты для задачи транспорта веществ на основе схем второго и четвертого порядков точности, которые показали, что для задачи диффузии-конвекции удалось повысить точность в 48,7 раз. Построенные схемы повышенного (четвертого) порядка точности были использованы при решении задач биологической кинетики. Предложен и численно реализован математический алгоритм, предназначенный для восстановления рельефа дна мелководного водоема на основе гидрографической информации (глубины водоема в отдельных точках или изолиний уровня), на основе которого была получена карта рельефа дна Азовского моря. Было установлено, что использование полей течений, рассчитанных по разработанной гидродинамической модели, позволило повысить качество входных данных, а также уменьшить значение погрешности при решении модельных задач биологической кинетики.

Статья в формате PDF

732 KB

схема повышенного порядка точности

рельеф дна

транспорт веществ

задачи биологической кинетики

многопроцессорная вычислительная система

1. Никитина А.В. Исследование моделей биологической кинетики // Известия ТРТУ. – 2005. – № 9(53). – С. 213.

2. Никитина А.В., Лозовская К.А. Численное моделирование процессов взаимодействия планктона и популяции промысловой рыбы пеленгас // Известия ЮФУ. Технические науки. 2011. – № 8. – С. 98–103.

3. Семенякина А.А. Схемы повышенного порядка точности для задач диффузии-конвекции // Информатика, вычислительная техника и инженерное образование. – 2013. – № 4 (15). – С. 18–29.

4. Сухинов А.И., Никитина А.В., Пескова О.Ю. Математическое моделирование процессов распространения загрязнений и эволюции фитопланктона применительно к акватории Таганрогского залива // Известия ТРТУ. – 2001. – № 2(20). – С. 32–36.

5. Сухинов А.И., Никитина А.В., Чистяков А.Е. Моделирование сценария биологической реабилитации Азовского моря // Математическое моделирование. – 2012. – Т. 24. – № 9. – С. 3–21.

6. Сухинов А.И., Никитина А.В., Чистяков А.Е., Семенов И.С. Математическое моделирование условий формирования заморов в мелководных водоемах на многопроцессорной вычислительной системе // Вычислительные методы и программирование. – 2013. – Т. 14. – С. 103–112.

7. Сухинов А.И., Чистяков А.Е. Параллельная реализация трехмерной модели гидродинамики мелководных водоемов на супервычислительной системе // Вычислительные методы и программирование: Новые вычислительные технологии. – 2012. – Т. 13. – С. 290–297.

8. Сухинов А.И., Чистяков А.Е., Проценко Е.А. Математическое моделирование транспорта наносов в прибрежной зоне мелководных водоемов // Математическое моделирование. – 2013. – Т. 25, № 12. – С. 65–82.

9. Сухинов А.И., Чистяков А.Е., Проценко Е.А. Математическое моделирование транспорта наносов в прибрежных водных системах на мнгопроцессорной вычислительной системе // Вычислительные методы и программирование. – 2014. – 15. – С. 610–620.

10. Сухинов А.И., Чистяков А.Е., Семенякина А.А., Никитина А.В. Параллельная реализация задач транспорта веществ и восстановления донной поверхности на основе схем повышенного порядка точности // Вычислительные методы и программирование: новые вычислительные технологии. – 2015. – Т. 16, № 2. – С. 256–267.

11. Сухинов А.И., Чистяков А.Е., Тимофеева Е.Ф., Шишеня А.В. Математическая модель расчета прибрежных волновых процессов // Математическое моделирование. – 2012. – Т. 24, № 8. – С. 32–44.

12. Сухинов А.И., Чистяков А.Е., Шишеня А.В. Оценка погрешности решения уравнения диффузии на основе схем с весами // Математическое моделирование. – 2013. – Т. 25, № 11. – С. 53–64.

13. Чистяков А.Е., Семенякина А.А. Применение методов интерполяции для восстановления донной поверхности // Известия ЮФУ. Технические науки. – 2013. – № 4. – С. 21.

Постановка задачи

Для реализации моделей биологической кинетики рассмотрим базовую задачу транспорта веществ следующего вида:

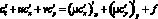
с граничными условиями

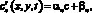
где u, v – компоненты вектора скорости; ? – коэффициент турбулентного обмена; f – функция, описывающая интенсивность и распределение источников.

Введем равномерную прямоугольную сетку [12]:

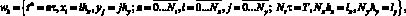
где ? – шаг по времени; hx, hy – шаги по пространству; Nx, Ny – границы по пространству; Nt – верхняя граница времени.

Проведем дискретизацию операторов конвективного и диффузионного переносов второго порядка погрешности аппроксимации в случае частичной заполненности ячеек следующим образом:

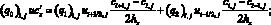
где qi – коэффициенты, описывающие заполненность контрольных областей [11].

Схемы повышенного порядка точности для операторов конвективного и диффузионного переносов

Аппроксимация оператора конвективного переноса uc? разностной схемой, обладающей четвертым порядком точности, имеет следующий вид [3]:

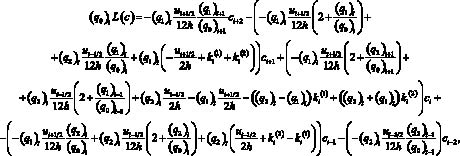
где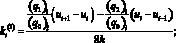

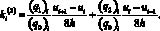
Аппроксимация оператора диффузионного переноса 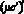разностной схемой, обладающей четвертым порядком точности, имеет следующий вид:

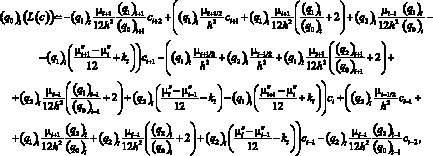
где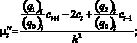

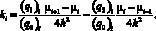
Сопоставление результатов расчета задачи транспорта веществ на основе схем второго и четвертого порядков точности

Погрешность вычислений рассчитывалась как разность между аналитическим и численным решением задачи транспорта веществ, начальное распределение задавалось функцией

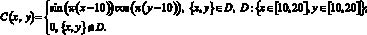
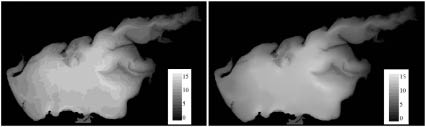
а б

Рис. 1. Исходная (а) и восстановленная (б) геометрия дна Азовского моря

Для моделирования использовались последовательно сгущающиеся сетки. На сетке размерами 100?100 расчетных узлов lx = 100 м, ly = 100 м, ht = 0,001 с; временной интервал равен 100 с, горизонтальная составляющая равна 4 м/с, вертикальная – 3 м/с, коэффициент турбулентного обмена равен 2 м2/с.

Из сопоставления результатов численных экспериментов на основе схем второго и четвертого порядков точности следует, что для задачи диффузии-конвекции удалось повысить точность в 48,7 раз [10].

Применение схем повышенного порядка точности для решения задач биологической кинетики для восстановления донной поверхности мелководного водоема

Работа с картографическими данными, обработка гидрографической информации являются достаточно актуальными задачами, возникающими при математическом моделировании гидродинамики мелководных водоемов [7]. Как показано на рис. 1, a, глубина водоема задается в отдельных точках или изолиниями уровня.

Использование подобных карт для построения расчетных сеток нежелательно, т.к. появляются погрешности вычислений, связанные с «грубым» заданием геометрии расчетной области. Для того чтобы повысить точности расчетов гидродинамических процессов, необходимо приблизить функцию двух переменных, описывающую рельеф дна водоема, более гладкими функциями. Для восстановления рельефа дна акватории Азовского моря использовался алгоритм, описанный в работе [13]. На основе разработанного программного комплекса получена карта рельефа дна Азовского моря (рис. 1, б).

Применение схем повышенного порядка точности для решения задач биологической кинетики

Методика восстановления донной поверхности и расчета полей течений водного потока в Азовском море была использована при решении модельных задач биологической кинетики. Рассчитанные поля течений использовались в качестве входной информации для моделей биологической кинетики [1] на примере задач: модель взаимодействия фито- и зоопланктона [4]; модель динамики промысловой рыбы пеленгас [2].

Использование разработанной модели гидродинамики с использованием схем повышенного порядка точности, разработанной методики восстановления донной поверхности мелководного водоема при решении вышеперечисленных задач привело к значительному уменьшению погрешности расчетов при численной реализации задач биологической кинетики.

Рис. 2. Динамика изменения концентрации зеленой водоросли для временных интервалов T = 2, 27, 39, 70, 85, 122 дня (после начала вегетационного периода фитопланктона (март – сентябрь))

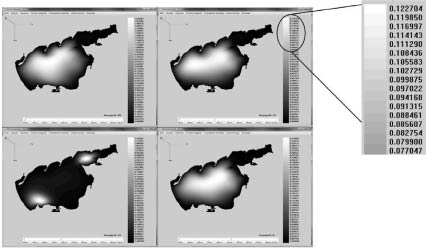
Рис. 3. Распределение концентраций пеленгаса, временной интервал T = 56, 126, 155, 400 дней. Начальное распределение полей течений в Азовском море для северного ветра

На рис. 2 показаны результаты численного эксперимента для задачи взаимодействия фито- и зоопланктона на основе полученных схем повышенного порядка точности для реальной расчетной области сложной формы – Азовского моря. На рис. 3 изображены результаты численного эксперимента на основе построенных схем повышенного порядка точности для задачи динамики промысловой рыбы пеленгас в Азовском море.

Заключение

Построены схемы повышенного (четвертого) порядка точности для операторов конвективного и диффузионного переносов, учитывающие заполненность ячеек. Выполнено сопоставление результатов расчета задачи транспорта веществ на основе схем второго и четвертого порядков точностей. Из сопоставления результатов численных экспериментов следует, что для задачи диффузии-конвекции удалось повысить точность в 48,7 раз. Предложен математический алгоритм, предназначенный для восстановления рельефа дна акватории мелководного водоема на основе гидрографической информации (глубины водоема в отдельных точках или изолиний уровня). На основе полученного метода решения задачи получена карта рельефа дна Азовского моря. Следует отметить, что предложенные схемы были так же применены для разработки программного комплекса, предназначенного для расчета трехмерных полей скоростей течений в мелководных водоемах, которые использовались в качестве входных данных при численной реализации задач биологической кинетики [5, 6] и транспорта донных материалов [8, 9].

Работа выполнена при частичной поддержке Задания №2014/174 в рамках базовой части государственного задания Минобрнауки России, а также при частичной финансовой поддержке РФФИ по проектам № 15-01-08619, № 15-07-08626 и № 15-07-08408.

Библиографическая ссылка