Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,798

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Сибгатуллин Э.С. 1 Исламов К.Ф. 1

---

1 Набережночелнинский институт (филиал) ФГАОУ ВПО «Казанский (Приволжский) федеральный университет»

В работе рассмотрена трёхслойная металлокерамическая пологая сферическая оболочка (два наружных слоя – из мягкой стали, внутренний слой – из магнезита). Опирание оболочки по контуру – шарнирное. Статическая внешняя нагрузка в виде сосредоточенной силы имеет произвольное направление и может быть приложена в любой точке оболочки. Решена задача о предельном состоянии оболочки (по прочности). Использован кинематический метод теории предельного равновесия. Для определения лучшей верхней оценки предельной нагрузки использован аппарат линейного программирования. Предварительно построены определённые сечения предельной поверхности для рассматриваемого слоистого материала в пространстве внутренних сил и моментов, которые аппроксимированы вписанными многогранниками, использован принцип максимума Мизеса для записи ограничений задачи линейного программирования. В результате решения задачи определены разрушающее значение внешней нагрузки и механизм разрушения оболочки.

Статья в формате PDF

726 KB

пологая сферическая оболочка

металлокерамика

предельная несущая способность по прочности

1. Гвоздев А.А. Расчет несущей способности конструкций по методу предельного равновесия. – М.: Стройиздат, 1949. – 280 с.

2. Работнов Ю.Н. Механика деформируемого твердого тела. – М.: Наука, 1979. – 744 с.

3. Сибгатуллин Э.С. Математическое моделирование прочности и несущей способности анизотропных и композитных элементов конструкций: дис. ... д-ра физ.-мат. наук. – Набережные Челны, 2001. – 405 с.

4. Сибгатуллин Э.С., Исламов К.Ф. Рациональное армирование железобетонного купола с вырезами // Вестник Тамбовского политехнического университета. Серия Естественные и технические науки. – Тамбов, 2006. – Т. 11. – Вып. 4. – С. 579–582.

5. Терегулов И.Г., Сибгатуллин Э.С. Критерий разрушения для многослойных композитных пластин и оболочек // Механика композитных материалов. – 1990. – № 1. – С. 74–79.

Расчёт элементов конструкций с использованием уравнений теории пластичности позволяет лучше использовать прочностные ресурсы материалов и конструкций, создавать экономически более выгодные изделия. Решение полной системы нелинейных уравнений теории пластичности в общем случае представляет собой сложную математическую задачу. Поэтому при определении несущей способности конструкций часто используют так называемые статический и кинематический методы теории предельного равновесия, основоположником которых является А.А. Гвоздев [1]. В данной работе для решения рассматриваемых задач использован кинематический метод.

В работе [2] получены параметрические уравнения гиперповерхности прочности (пластичности) для слоистых гибридных композитных оболочек и пластин в пространстве обобщенных сил T_mi:

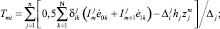
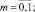
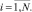(1)

В случае кратковременного статического нагружения, например, эти уравнения принимают следующий вид:

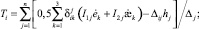
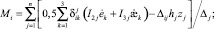
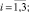
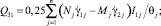(2)

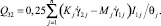
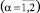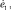
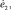
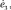
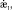
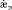
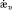
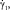
Здесь и далее T_α ≡ T_αα, M_α ≡ M_αα , T₃ ≡ T₁₂, M₃ ≡ M₁₂, Q₃₁, Q₃₂ – обобщенные силы; 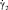– скорости соответствующих обобщенных перемещений; h_j – толщина j-го слоя; z_j – координата срединной поверхности j-го слоя (в системе α₁α₂z, ось z перпендикулярна поверхности приведения S₀ оболочки, рис. 1); z_1j < z_2j – координаты наружных поверхностей j-го слоя.

Определение несущей способности металлокерамической сферической оболочки выполняем с использованием варианта кинематического метода, описанного в работе [2].

В данном методе предполагается, что разрушение конструкции происходит вдоль отдельных бесконечно тонких слоев, перпендикулярных поверхности приведения S₀, а области между ними остаются «жесткими».

Уравнение баланса мощностей имеет следующий вид [2]:

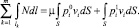(3)

Здесь l_k – длина k-й линии разрушения; m – число линий разрушения; S – площадь поверхности приведения сил; N – мощность внутренних обобщенных сил, приходящаяся на единицу длины линии разрушения; v_i – компоненты вектора скорости движения точки оболочки, где приложена сила p_i; μ – параметр, пропорционально которому растут внешние нагрузки. По повторяющемуся индексу i (i = 1, 2, 3) производится суммирование.

Предельную поверхность аппроксимируем выпуклым многогранником, i-ая вершина которого определяется вектором 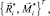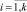, k – число вершин аппроксимирующего многогранника. Здесь R_i, M_i – погонные силы и моменты, приложенные к сечению поверхности S₀.

На мощности погонных внутренних сил и моментов на концах линий разрушения O₁O₂ (рис. 1), развиваемые ими на разрывах скоростей соответствующих перемещений и поворотов, согласно постулату Друккера [2], можно наложить следующие ограничения [3]:

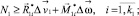
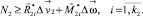(4)

Здесь k₁, k₂ – количество вершин предельных многогранников, подходящих точкам О₁ и О₂ соответственно.

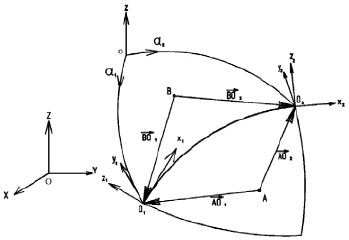
Рис. 1. Схема расположения линии разрушения O₁O₂ на границе абсолютно жёстких конечных элементов

Вдоль линий разрушения используем линейную аппроксимацию функции N. В итоге получаем следующую задачу линейного программирования: найти min m⁺, где

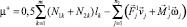(5)

при условии

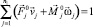(6)

и при соблюдении ограничений вида (4). Здесь j – номер жесткого элемента; n₁ – число жестких элементов, на которые действуют нагрузки, зависящие от параметра m; n₂ – число жестких элементов, на которые действуют нагрузки, не зависящие от параметра m. Здесь внешние силы, действующие в пределах отдельного жесткого диска, приведены к его полюсу. Результатом этого являются сосредоточенные силы 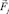и сосредоточенные моменты 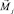, приложенные к соответствующим полюсам.

Рассмотрим трёхслойную составную оболочку с относительно небольшой стрелой подъёма, где два наружных слоя стальные, внутренний слой – керамический.

Характеристики слоёв приведены в табл. 1.

С использованием уравнений (2) были построены некоторые сечения гиперповерхности прочности для трёхслойной оболочки (рис. 2, 3, 4). Алгоритм построения аналогичных сечений проведён, например, в [4].

На рис. 5 показана проекция металлокерамической сферической оболочки с радиусом 1,3 м и диаметром опорной окружности 1 м на плоскость XОY (рис. 1), нагруженной в точке 5 сосредоточенной силой, направляющие косинусы которой равны (0,5; 0,5; –0,7071); общая толщина оболочки – 22 мм; опирание – шарнирное по контуру. Здесь же показано разбиение на жёсткие элементы и линии разрушения между ними. Прочностные характеристики слоёв и их толщины приведены в табл. 1.

Таблица 1

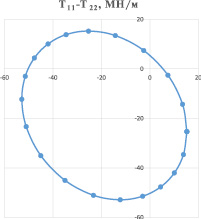
Рис. 2. Сечение гиперповерхности прочности плоскостью T₁₁–T₂₂, (МН/м)

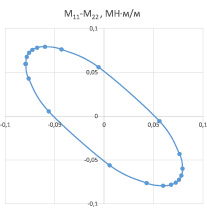
Рис. 3. Сечение гиперповерхности прочности плоскостью М₁₁–М₂₂, (МН∙м/м)

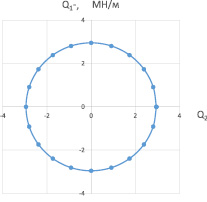
Рис. 4. Сечение гиперповерхности прочности плоскостью Q₁–Q₂, (МН/м)

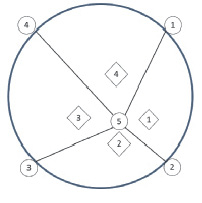
Рис. 5. Схема абсолютно жёстких конечных элементов

Таблица 2

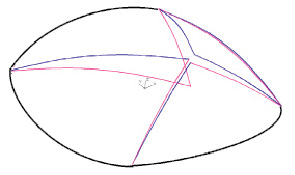
Рис. 6. Схема перемещений АЖКЭ

В результате решения соответствующей задачи линейного программирования получено значение μ⁺ = 6,9686 МН. В табл. 2 приведены соответствующие скорости перемещений полюсов жестких дисков v_x, v_y, v_z и их поворотов ω_x, ω_y, ω_z относительно полюсов.

На рис. 6 показаны линии разрушения, построенные с использованием табл. 2.

На рис. 7 приведена схема распределения N вдоль линий разрушения, построенная с использованием табл. 3.

Здесь N₁ и N₂ являются мощностями, развиваемыми на концах линий разрушения; они имеют размерность МН/с.

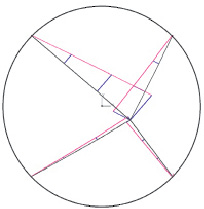
Рис. 7. Эпюры N

Таблица 3

В заключение отметим, что составленные нами соответствующие алгоритм и программа для ЭВМ позволяют достаточно эффективно решать задачи, аналогичные рассмотренной выше.

Рецензенты:

Астащенко В.И., д.т.н., профессор кафедры материалов, технологий и качества, Набережночелнинский институт (филиал) ФГАОУ ВПО «Казанский (Приволжский) федеральный университет», г. Набережные Челны;

Панкратов Д.Л., д.т.н., профессор кафедры машиностроения, Набережночелнинский институт (филиал) ФГАОУ ВПО «Казанский (Приволжский) федеральный университет», г. Набережные Челны.

Библиографическая ссылка