Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Третьяков А.А. 1

---

1 ФГБОУ ВПО «Челябинская государственная агроинженерная академия»

В работе рассмотрена задача о вдавливании конического индентора в плоскую поверхность упругопластического тела. Исследовано влияние усилия вдавливания и свойств материала контртела на геометрические параметры наплыва вокруг остаточного отпечатка. Обозначена актуальность исследования. Представлена программа исследований. Приведены результаты расчетов для различных комбинаций свойств материала. Представлены основные графики зависимостей диаметра и максимальных перемещений в наплыве от усилия вдавливания конуса и максимального перемещения от диаметра отпечатка. Получены выражения, описывающие закономерности образования диаметра и формирования наплыва остаточного отпечатка. В результате проведенных исследований разработана математическая модель, описывающая закономерности формирования наплыва вокруг отпечатка конического индентора с учетом параметров нагружения и механических свойств материала детали.

Статья в формате PDF

1065 KB

конический индентор

упругопластическое тело

контактная задача

1. А.с. 1158855 СССР, МКИ G 01 В 5/30. Способ оценки остаточных напряжений / О.П. Осташ, Б.М. Зайдель, В.Т. Жмур–Клименко // Открытия. Изобретения. – 1985. – № 20.

2. Джонсон К. Механика контактного взаимодействия. – М.: Мир, 1989. – 510 с.

3. Игнатьев А.Г. Диагностирование поверхностных остаточных напряжений в металлических покрытиях, нанесенных при восстановлении деталей: автореф. дис. … д-ра техн. наук. − Челябинск, 2008. – 40 с.

4. Качанов Л.М. Основы теории пластичности. – М.: Наука, 1969. – 420 с.

5. Третьяков А.А. Исследование профиля наплыва при вдавливании конического индентора в плоскую поверхность упругопластического тела // Современные проблемы науки и образования. – 2013. – № 6; URL: http://www.science-education.ru/113-10793 (дата обращения: 15.11.2013).

6. Третьяков А.А. Влияние усилия вдавливания конуса в поверхность упругопластического тела и механических свойств материала детали на диаметр отпечатка // Вестник Совета молодых учёных и специалистов Челябинской области. – 2013. – № 1. – 88 с.

7. Филин А.П. Прикладная механика твердого деформируемого тела. – М.: Наука, 1975. – Т. 1. – 832 с.

Основные практические направления исследований в области механики контактного взаимодействия относятся к проблемам трения, износа, разрушения контактирующих элементов, измерения твердости, механических свойств материалов и др. В связи с этим интенсивно выявляются и изучаются закономерности деформирования в различных видах контактных задач.

Неупругое контактное взаимодействие тел является существенно менее исследованной областью механики по сравнению с упругой задачей. Достаточно развиты решения для контакта идеально-упругопластических и идеально-жесткопластических тел [1]. Для упругопластического упрочняющегося материала решение задачи связано со значительными трудностями, связанными, в частности, с отсутствием информации о форме и размерах упругопластической границы. Поэтому основные результаты в данной задаче получены численными методами [4]. При этом основное внимание уделяется зарождению пластического течения, контактным напряжениям и усилиям, распределениям напряжений в контактирующих телах, геометрическим параметрам контакта. Количественные данные о деформированном состоянии поверхности в области контакта недостаточны. Это, в первую очередь, относится к геометрическим параметрам наплыва, формирующегося вокруг отпечатка. Признавая наличие наплыва, его подвергают анализу исключительно с точки зрения влияния на измеряемый диаметр отпечатка [2].

В связи с этим для описания механизма формирования наплыва вокруг отпечатка, для выявления влияния различных факторов на его параметры, для качественного и количественного описания начального напряженного состояния необходимо проведение дополнительных исследований.

Задача о вдавливании индентора в плоскую поверхность упругопластического тела рассматривается в цилиндрической системе координат (рис. 1). Оси r и θ лежат в плоскости, совпадающей с поверхностью контртела, ось z направлена перпендикулярно плоскости контртела. Начало координат находится в точке начального контакта до приложения контактной нагрузки [7].

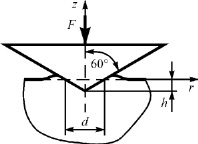
Рис. 1. Система координат в задаче о вдавливании конического индентора

Моделирование задачи о вдавливании жесткого конуса в упругопластическое тело с использованием метода конечных элементов и проверка контактного алгоритма представлены в работе [5]. Целью моделирования вдавливания конуса в упругопластичное тело является исследование влияния усилия вдавливания индентора и свойств материала детали (предел текучести σти модуль упрочнения Eт) на основные геометрические характеристики остаточного отпечатка (диаметр d и максимальные нормальные перемещения в наплыве W).

Матрица исследования деформированного состояния поверхности вокруг отпечатка индентора для ненапряженной однородной детали представлена в табл. 1.

Для каждого из материалов проведена серия расчетов с различными величинами усилия вдавливания. Фиксировали: диаметр остаточного отпечатка d, величину максимального нормального перемещения в наплыве Wmax, координату точки с максимальным нормальным перемещением rmax. На основании этих данных для каждой комбинации механических свойств материала с использованием регрессионного анализа определяли зависимости d(F), Wmax(d), Wmax(F). Из полученных зависимостей выведены зависимости d(F, σт, Eт), Wmax(d, σт, Eт), Wmax(F, σт, Eт), которые впоследствии были представлены в относительном виде d2/d1 = f(σт1, σт2, Eт1, Eт2), Wmax2/Wmax1 = f(σт1, σт2, Eт1, Eт2). Т.е. были получены выражения, с помощью которых можно определить изменение геометрических параметров d и Wmax для материала с индексом 2 по отношению к некоему материалу с индексом 1. Такой подход можно считать оправданным, поскольку данные для базового материала получаются экспериментальным путем. Зависимости в относительном виде и получение данных для какого-либо материала в сравнении с базовым позволит получить более точный результат, нежели прямое определение параметров по приближенным зависимостям.

Таблица 1

Матрица исследования

Влияние усилия вдавливания индентора на геометрические характеристики наплыва представлено на рис. 2. Увеличение усилия вдавливания индентора F вызывает рост диаметра отпечатка d (рис. 2, а) при неизменных свойствах материала (значениях предела текучести σт и модуля упрочнения Eт), а также увеличение максимального нормального перемещения в наплыве Wmax (рис. 2, б). Соответственно, увеличение диаметра отпечатка приводит к возрастанию перемещения Wmax (рис. 2, в).

Общие закономерности изменения диаметра отпечатка для всех исследованных комбинаций свойств материалов следующие [3, 6]:

1) связь между усилием вдавливания F и диаметром отпечатка d с погрешностью, не превышающей 1,5 % по отношению к данным расчетов, описывается регрессионной зависимостью

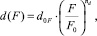(1)

где d0F – условный диаметр отпечатка (мм), возникающий при единичном усилии вдавливания F0, равном 1 Н;

2) влияние механических свойств на величину показателя степени nd в уравнении (1) незначительно, вполне допустимо принять его постоянным;

3) влияние механических свойств материала на диаметр отпечатка проявляется в изменении условного диаметра d0F (табл. 2).

Eт = 5·103 МПа, 1 – σт = 250 МПа, 2 – σт = 400 МПа, 3 – σт = 800 МПа, 4 – σт = 1000 МПа,

σт = 800 МПа, 1 – Eт = 0,5·104 МПа, 2 – Eт = 0,8·104 МПа, 3 – Eт = 1·104 МПа, 4 – Eт = 1,5·104 МПа

а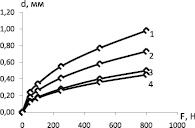

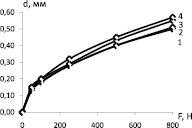
Eт = 1·104 МПа, 1 – σт = 250 МПа, 2 – σт = 400 МПа, 3 – σт = 800 МПа, 4 – σт = 1000 МПа

σт = 400 МПа, 1 – Eт = 0,5·104 МПа, 2 – Eт = 0,8·104 МПа, 3 – Eт = 1·104 МПа, 4 – Eт = 1,5·104 МПа

б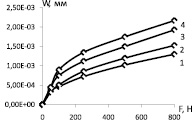

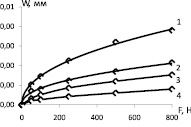
Eт = 1,5·104 МПа, 1 – σт = 250 МПа, 2 – σт = 40 МПа, 3 – σт = 800 МПа, 4 – σт = 1000 МПа

σт = 1000 МПа, 1 – Eт = 0,5·104 МПа, 2 – Eт = 0,8·104 МПа, 3 – Eт = 1·104 МПа, 4 – Eт = 1,5·104 МПа

в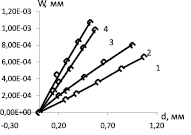

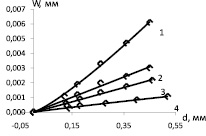
Рис. 2. Влияние усилия вдавливания индентора: а – влияние усилия вдавливания индентора на диаметр отпечатка; б – влияние усилия вдавливания индентора на максимальное перемещение в наплыве; в – влияние диаметра отпечатка на максимальное перемещение в наплыве

Таблица 2

Коэффициенты уравнений регрессии, описывающих зависимость диаметра отпечатка от усилия вдавливания при разных механических свойствах материала контртела

Относительное изменение условного диаметра отпечатка d0F в зависимости от соотношений механических свойств материалов имеет вид

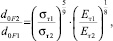(2)

где индексы 1 и 2 имеют отношение к материалам со свойствами (σт1, Ет1) и (σт2, Ет2).

Если в качестве материала 1 использовать условный материал с пределом текучести σту = 1 МПа и модулем упрочнения Eтy = 1 МПа, для которого при аппроксимации расчетных данных получено значение условного диаметра отпечатка d0Fу = 0,31 мм при усилии вдавливания индентора Fу = 1 Н, то диаметр отпечатка для искомого материала определится как

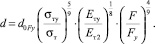(3)

Преобразуя выражения (2) и (3), получим:

1) отношение диаметров отпечатков и пределов текучести позволяет определить отношение модулей упрочнения:

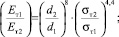(4)

2) по измеренному диаметру отпечатка, известной нагрузке вдавливания и известному пределу текучести можно определить модуль упрочнения материала с погрешностью 10 %:

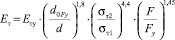. (5)

При анализе влияния механических свойств материала детали на нормальные перемещения W в наплыве имеет смысл рассматривать зависимость нормальных перемещений в наплыве в первую очередь от диаметра отпечатка. Исключение из разрешающих уравнений силового фактора целесообразно с практической точки зрения.

Для всех исследованных материалов связь между максимальным перемещением в наплыве Wmax и диаметром отпечатка с погрешностью, не превышающей 3 %, описывается регрессионной зависимостью

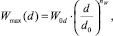(6)

где W0d – условное максимальное перемещение (мм), возникающее при диаметре отпечатка d0 = 1 мм. Влияние механических свойств материала (σт и Eт) на высоту наплыва проявляется через изменение условного максимального перемещения W0d и показателя степени nW (табл. 3).

Изменение условного перемещения W0d и показателя степени nW в зависимости от предела текучести и модуля упрочнения показано на рис. 3.

Данные, приведенные в табл. 3 и на рис. 3, показывают, что при анализе влияния механических свойств на максимальные нормальные перемещения в наплыве необходимо учитывать как изменение условного перемещения W0d, так и изменение показателя степени nW.Общую тенденцию относительного изменения условного перемещения W0d и показателя степени nW в зависимости от соотношения механических свойств материалов описывают приближенные выражения

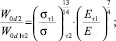(7)

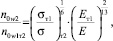(8)

где индексы 1 и 2 имеют отношение к материалам со свойствами (σт1, Ет1) и (σт2, Ет2).

Анализ результатов расчетов показал, что преобразование выражений (7) и (8) при дальнейшем регрессионном анализе позволят определить изменение отношений условных перемещений, зависимость абсолютной величины условного перемещения W0d от механических свойств материала, изменение отношения показателей степени nW2/nW1, зависимость абсолютного значения показателя степени nW от механических свойств материала.

Таблица 3

Коэффициенты уравнений регрессии в виде (6), описывающих зависимость максимального перемещения от диаметра отпечатка при разных механических свойствах материала контртела

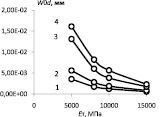
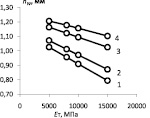
Рис. 3. Зависимость условного перемещения W0d и показателя степени nW от механических свойств материала: 1 – σт = 250 МПа; 2 – σт = 400 МПа; 3 – σт = 800 МПа; 4 – σт = 1000 МПа

Заключение

В результате проведенных исследований получена математическая модель, описывающая закономерности формирования наплыва вокруг отпечатка конического индентора с учетом параметров нагружения и механических свойств материала детали. Установлены закономерности образования диаметра отпечатка, описываемые выражениями (1), (2), (3), которые позволяют определить величину модуля упрочнения материала по выражениям (4) и (5) и закономерности формирования наплыва вокруг отпечатка, описываемые диаграммой вдавливания «Wmax – d» в виде (6).

Рецензенты:

Ерофеев В.В., д.т.н., профессор, заведующий кафедрой «Технология и организация технического сервиса», ФГБОУ ВПО «Челябинская государственная агроинженерная академия», г. Челябинск;

Плаксин А.М., д.т.н., профессор, кафедра «Эксплуатация машин транспортного парка», ФГБОУ ВПО «Челябинская государственная агроинженерная академия», г. Челябинск.

Работа поступила в редакцию 19.12.2013.

Библиографическая ссылка