В работе приводится продолжение исследований, выполненных в [1]. Рассматривается решение осесимметричной задачи термоупругости, когда на внутренней и внешней поверхностях области происходит теплообмен со средой по закону Ньютона, а также анализируется влияние температурного поля на характер разрушения – жесткое разрушение путем отрыва или мягкое разрушение путем среза.
При оценке термопрочности деталей машин в условиях стационарного и циклического нагружений сравнительно мало проанализировано влияние коэффициентов теплопередачи и скорости нагрева на величину напряжений и деформаций, а также характер разрушения деталей. Для решения данной проблемы используется классическое изложение вопросов теплопередачи [2, 3], определения температурных напряжений при различных типах граничных условий для температуры [4, 5], а также разрушения материала и деталей при температурных воздействиях [6]. Представляет также интерес решение новых конкретных задач при граничных условиях третьего рода для температуры, позволяющих оценить влияние скорости нагрева на характер разрушения деталей, системный анализ влияния параметров нагружения на напряженное состояние деталей, что и рассматривается в данной статье.
Данные исследования имеют важное прикладное значение для определения термопрочности таких деталей, как валки прокатных станов, ролики машин непрерывного литья, другие детали металлургического оборудования, работающие при повышенных температурах.
Анализ на примере длинного цилиндра
Анализ стационарного нагружения выполнен на примере длинного цилиндра при осесимметричном температурном поле. При этом R1, R2 – внутренний и внешний радиусы цилиндра; p1, p2 – давление на внутренней и внешней поверхностях; T(r) – стационарное температурное поле. Следуя [7], получим распределение напряжений в цилиндре:
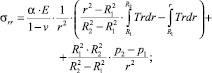 (1)
(1)
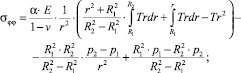 (2)
(2)
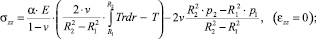 (3)
(3)
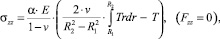 (4)
(4)
где α – коэффициент линейного расширения; Е – модуль упругости; v – коэффициент Пуассона. Формула (3) соответствует плоскому деформированному состоянию, а (4) – случаю равенства нулю осевого усилия, причем при p1 = p2 = 0 и σzz = σrr + σφφ.
Стационарное температурное поле внутри цилиндра при граничных условиях третьего рода, когда на внутренней и внешней поверхностях происходит теплообмен со средой по закону Ньютона, определяется выражением:
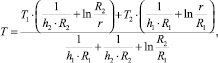 (5)
(5)
где 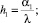
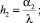 Т2 – температура среды на внутренней и внешней поверхностях; α1, α2 – коэффициенты теплоотдачи на внешней и внутренней поверхностях, Вт/(м2∙град.); λ – коэффициент теплопроводности материала, Вт/(м2∙град.).
Т2 – температура среды на внутренней и внешней поверхностях; α1, α2 – коэффициенты теплоотдачи на внешней и внутренней поверхностях, Вт/(м2∙град.); λ – коэффициент теплопроводности материала, Вт/(м2∙град.).
Результаты расчетов для цилиндра при изменении коэффициента теплоотдачи на внешней поверхности и внутреннего радиуса цилиндра приведены в табл. 1. При этом значения остальных величин, входящих в формулы, приняты равными: Е = 0,196∙106 МПа; v = 0,35; α = 11,4∙10–6 град–1; R2 = 0,175 м; T2 = 250 °C; h1 = 40 м–1; Т1 = 90 °С.
В табл. 2.1 и 2.2 приведено распределение температуры, напряжений и коэффициента m, характеризующего характер напряженного состояния, по радиусу. Коэффициент m, согласно объединенной теории прочности Давиденкова-Фридмана, характеризует напряженное состояние и представляет собой отношение наибольшего касательного напряжения к наибольшему приведенному растягивающему напряжению в данной точке:
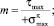
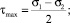
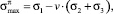
причем σ1 – наибольшее; σ3 – наименьшее главные напряжения.
Вместе с сопротивлениями отрыву и срезу коэффициент m характеризует возможность хрупкого или вязкого разрушения. При «жестких» способах нагружения m < 1 более вероятным является хрупкое разрушение путем отрыва, когда может быть использована теория наибольших удлинений. При «мягких» – разрушение путем среза после довольно значительной пластической деформации, когда можно применять теорию наибольших касательных напряжений.
Таблица 1
Значения температуры и напряжений (МПа) на внешней и внутренней поверхностях цилиндра, R2 = 0,175 м; h1 = 40 м–1; T1 = 90 °C; T2 = 250 °C
|
Внутренний радиус R1, м |
|||||||
|
0,125 |
0,0875 |
0,0475 |
|||||
|
r = R1 |
r = R2 |
r = R1 |
r = R2 |
r = R1 |
r = R2 |
||
|
σφφ |
61 |
–49 |
110 |
–70 |
174 |
–72 |
|
|
h2 = 5 м–1 |
σzz |
–222 |
–332 |
–211 |
–390 |
–206 |
–452 |
|
T,°C |
109 |
141 |
111 |
164 |
119 |
191 |
|
|
σφφ |
158 |
–126 |
213 |
–135 |
260 |
–108 |
|
|
h2 = 50 м–1 |
σzz |
–256 |
–540 |
–220 |
–569 |
–209 |
–577 |
|
T,°C |
140 |
222 |
132 |
233 |
134 |
241 |
|
|
σφφ |
173 |
–139 |
225 |
–143 |
267 |
–111 |
|
|
h2 = 100 м–1 |
σzz |
–261 |
–573 |
–221 |
–589 |
–209 |
–587 |
|
T,°C |
144 |
235 |
134 |
241 |
135 |
245 |
|
|
σφφ |
188 |
–150 |
236 |
–149 |
273 |
–114 |
|
|
h2 = 500 м–1 |
σzz |
–266 |
–604 |
–222 |
–607 |
–209 |
–596 |
|
T,°C |
148 |
247 |
136 |
248 |
136 |
249 |
|
Таблица 2.1
Распределение температуры, напряжений и коэффициента m по радиусу цилиндра, R1 = 0,125 м; R2 = 0,175 м; T1 = 90 °C; T2 = 250 °C; h1 = 40 м–1; h2 = 50 м–1
|
Текущий радиус r, м |
||||||
|
0,125 |
0,135 |
0,145 |
0,155 |
0,165 |
0,175 |
|
|
Т, °С |
139 |
158 |
176 |
192 |
207 |
222 |
|
σrr, МПа |
0 |
9 |
12 |
11 |
6 |
0 |
|
σφφ, МПа |
158 |
84 |
21 |
–34 |
–83 |
–126 |
|
σzz, МПа (εzz = 0) |
–256 |
–321 |
–381 |
–437 |
–490 |
–540 |
|
m |
0,84 |
1,05 |
1,34 |
1,27 |
1,2 |
1,16 |
|
σzz, МПа (Fz = 0) |
158 |
93 |
33 |
–24 |
–77 |
–126 |
|
m |
0,77 |
0,69 |
0,49 |
0,72 |
0,72 |
0,71 |
Таблица 2.2
Распределение температуры, напряжений и коэффициента m по радиусу цилиндра, R1 = 0,0875 м; R2 = 0,175 м; T1 = 90 °C; T2 = 250 °C; h1 = 40 м–1; h2 = 50 м–1
|
Текущий радиус r, м |
||||||
|
0,088 |
0,105 |
0,122 |
0,14 |
0,157 |
0,175 |
|
|
Т, °С |
132 |
158 |
181 |
201 |
218 |
233 |
|
σrr, МПа |
0 |
25 |
29 |
23 |
13 |
0 |
|
σφφ, МПа |
213 |
97 |
15 |
–46 |
–95 |
–135 |
|
σzz, МПа (εzz = 0) |
–220 |
–312 |
–389 |
–456 |
–516 |
–569 |
|
m |
0,75 |
1,04 |
1,23 |
1,2 |
1,16 |
1,15 |
|
σzz, МПа (Fz = 0) |
213 |
122 |
44 |
–23 |
–82 |
–135 |
|
m |
0,77 |
0,61 |
0,51 |
0,72 |
0,72 |
0,71 |
Результаты расчетов показывают, что цилиндр с равным нулю осевым усилием характеризуется более жестким напряженным состоянием, когда наиболее вероятным является разрушение путем отрыва. Следует отметить, что при расчетах на термопрочность температурное поле оказывает влияние на величину напряжений в соответствующей точке, сопротивление отрыву и срезу и характер разрушения, который определяется коэффициентом напряженного состояния m.
При анализе температурных напряжений представляет интерес влияние коэффициентов теплоотдачи h1 и h2, размера внутреннего отверстия R1 на величину напряжений.
Из данных табл. 1 следует, что при фиксированном значении R1 = 0,125 м увеличение коэффициента теплоотдачи h2 с 5,0 до 500 м–1 увеличивает перепад температур на внешней и внутренней поверхностях и, соответственно, тангенциальные напряжения с 61 до 188 МПа на внутренней поверхности и с –49 до –150 МПа на наружной поверхности, подтверждая тот факт, что более теплоизолированный цилиндр обладает большей термопрочностью. Уменьшение размера внутреннего отверстия во всех случаях приводит к увеличению тангенциальных напряжений на внутренней поверхности. При h1 = 5 м–1 сжимающие тангенциальные напряжения на внешней поверхности увеличиваются по абсолютной величине, в других случаях происходит уменьшение по абсолютной величине при уменьшении размера внутреннего отверстия. Если температуры на внешней и внутренней поверхности 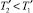 , то тангенциальные напряжения будут сжимающими на внутренней поверхности и растягивающими на внешней. Можно отметить, что с точки зрения величины напряжений на внутренней и внешней поверхностях при различных температурах, наиболее прочным является цилиндр с большим размером внутреннего отверстия.
, то тангенциальные напряжения будут сжимающими на внутренней поверхности и растягивающими на внешней. Можно отметить, что с точки зрения величины напряжений на внутренней и внешней поверхностях при различных температурах, наиболее прочным является цилиндр с большим размером внутреннего отверстия.
Результаты расчетов, приведенные в табл. 2.1 и 2.2, позволяют отметить следующее. При R1 = 0,125 м и R1 = 0,0875 м тангенциальные напряжения σφφ достаточно быстро уменьшаются по мере удаления от внутренней и наружной поверхностей цилиндра. Так же ведут себя осевые напряжения σzz при равном нулю осевом усилии Fz = 0.
Для плоского деформированного состояния εzz = 0 осевые напряжения достигают наибольшего значения по абсолютной величине на наружной поверхности. В этом случае коэффициент m, определяющий характер напряженного состояния, имеет наименьшее значение на внутренней поверхности, где наиболее вероятно хрупкое разрушение путем отрыва. При данном значении температурного поля в центральной части полого цилиндра наблюдается переход к более мягкому виду напряженного состояния и разрушению путем среза, а на наружной поверхности возможен тот и другой вид разрушения. При равном нулю осевом усилии Fz = 0 во всех точках цилиндра m < 1, что определяет наиболее вероятное хрупкое разрушение путем отрыва. Следует отметить, что наименьшее значение коэффициента m имеет место во внутренних точках области, когда напряженное состояние приближается к всестороннему равномерному растяжению.
Рецензенты:
Паршин В.С., д.т.н., профессор, заведующий кафедрой «Металлургические и роторные машины» Механико-машиностроительного института Уральского федерального университета им. первого Президента России Б.Н. Ельцина, г. Екатеринбург;
Чечулин Ю.Б., д.т.н., профессор кафедры «Детали машин» Механико-машиностроительного института Уральского федерального университета им. первого Президента России Б.Н. Ельцина, г. Екатеринбург;
Пындак В.И., д.т.н., профессор Волгоградской сельскохозяйственной академии, г. Волгоград.
Работа поступила в редакцию 03.06.2013.
Библиографическая ссылка
Артемьева Е.А., Денисов Ю.В. АНАЛИЗ ВЛИЯНИЯ ТЕМПЕРАТУРНЫХ ПОЛЕЙ НА ХАРАКТЕР РАЗРУШЕНИЯ ДЕТАЛЕЙ // Фундаментальные исследования. 2013. № 6-6. С. 1329-1332;URL: https://fundamental-research.ru/ru/article/view?id=31735 (дата обращения: 29.01.2026).



