Одним из перспективных способов, развивающих принципы селективного разрушения двухкомпонентных тел, является виброразрушение в конусном виброизмельчителе инерционного типа с одновременной воздушной сепарацией продуктов разрушения.
Подлежащий измельчению сыпучий материал подают в кольцевой зазор между неподвижным и подвижным конусами виброизмельчителя. Находясь в состоянии виброкипения, частицы материала подвергаются разрушению. На тело воздействует циклическая нагрузка, создаваемая центробежной силой дебалансов, вызывая основные сжимающие и сдвиговые усилия. Величина деформации слоя сыпучего материала регулируется зазором между конусами. Виброизмельчитель включён в систему аспирации, которая содержит циклон, фильтр и вытяжной вентилятор.
Для исследования процесса селективного измельчения воспользуемся теорией цепей Маркова. Рассмотрим процесс разрушения сыпучей среды, состоящей из бикомпонентных частиц, представляющих собой сфероиды, заключённые один в другом и не связанных между собой, причём работа разрушения внешнего компонента меньше, чем для внутреннего.
Изменение состояния сыпучей среды можно представить графом состояний, представленном на рисунке 1:
где С0 - начальное состояние сыпучей среды, состоящей из двухкомпонентных твёрдых тел; Сn - промежуточное состояние сыпучей среды, когда произошло частичное отделение компонентов друг от друга; С1 - конечное состояние разрушенной силовым воздействием внешнего компонента; C2 - конечное состояние отделённого внутреннего компонента; λij - интенсивность перехода из состояния Ci в состояние Cj.
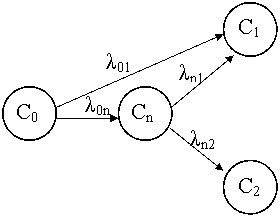
Рисунок 1. Граф состояний.
Граф состояний описывается дифференциальными уравнениями:
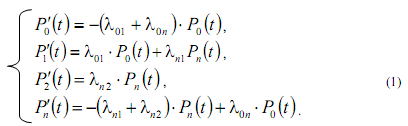
Начальные условия:
![]()
Условие нормировки:
![]() .
.
В соответствии с начальными условиями при ![]() :
:
![]() ,
, ![]() .
.
Решая систему дифференциальных уравнений (1) при заданных начальных условиях, выявляем функциональную зависимость вероятностей Pi от интенсивности λij:
![]() ,
,
![]() , (2)
, (2)
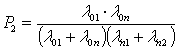 .
.
Необходимо также учитывать, что отделённая оболочка, находясь в помольной камере измельчителя, разрушается, образуя дополнительную поверхность. Следовательно, можно записать, что:
![]() ,
,
![]() , (3)
, (3)
где λS - скорость селективного измельчения; λ1 - скорость прирастания поверхности отделённой от ядра оболочки.
Подставив (3) в выражение (2), после очевидных преобразований получим:
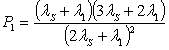 ,
,
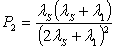 . (4)
. (4)
Скорость образования новой поверхности является кинетической функцией измельчения. Функция измельчения связана с распределительной функцией f(x), где x - текущий характерный размер частиц среды. Функция изменения поверхности f(S) сыпучей среды связана с распределительной функцией выражением:
![]() ,
,
где k - коэффициент формы частиц среды.
Пусть характер распределения энергии по частицам задан функцией F(S). Тогда затраты энергии на образование новой поверхности составят:
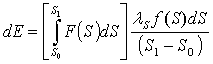 , (5)
, (5)
где S0 - начальная поверхность совместного существования компонентов в частицах; S1 - конечная площадь поверхности частиц с учётом её разрушения.
На основании работы [1], будем считать, что энергия E, подводимая к материалу распределяется пропорционально содержанию фракций:
![]() . (6)
. (6)
Приравняем формулы (5) и (6) и выразим кинетическую функцию селективного измельчения λS:
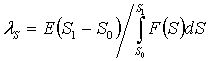 . (7)
. (7)
Функция F(S) по своей сущности является энергетическим законом разрушения твердых дел. Для случая селективного разрушения наиболее приемлем закон Риттингера, согласно которому энергия разрушения пропорциональна вновь образованной поверхности. Следовательно, F(S) имеет вид:
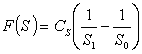 , (8)
, (8)
где CS - размерный коэффициент пропорциональности, учитывающий распределение энергии, как в отдельных частицах, так и в сыпучей среде в процессе разрушения, имеющий размерность [Дж·c]. CS можно представить в следующем виде:
![]() , (9)
, (9)
где Е - подводимая рабочими органами энергия; А1 - работа деформации и разрушения внешнего компонента; U - энергия упругой деформации внутреннего компонента; D - диссипативные потери энергии на трение и пр.; m0 - начальное количество частиц материала; e-βt - функция уменьшения количества неразрушенных частиц во времени; t - текущее время; β - численный параметр, определяемый эмпирически.
Проведя подстановку (8) в (7) и интегрирование, получим выражение для кинетической функции селективного разрушения:
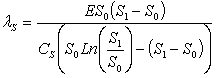 . (10)
. (10)
Подстановка (10) в (4) позволяет получить математическую модель, связывающую вероятностное определение возможности разрушения материала с кинетической энергией рабочего органа машины и прочностными свойствами материала.
СПИСОК ЛИТЕРАТУРЫ
- Мизонов, В.Е. Некоторые закономерности селективного измельчения //Теоретические основы химической технологии. - 1984. -Т. 18, № 3. - С. 410 - 411.
Библиографическая ссылка
Руднев С.Д., Сяглов А.С., Клеников Д.В. МОДЕЛИРОВАНИЕ ПРОЦЕССА СЕЛЕКТИВНОГО РАЗРУШЕНИЯ ДВУХКОМПОНЕНТНЫХ ТЕЛ В КОНУСНОМ ВИБРОИЗМЕЛЬЧИТЕЛЕ // Фундаментальные исследования. 2005. № 4. С. 86-88;URL: https://fundamental-research.ru/ru/article/view?id=6024 (дата обращения: 04.07.2025).



