Нестационарный процесс теплового разгона чаще всего наблюдается в никель-кадмиевых аккумуляторах, эксплуатирующихся в буферном режиме, в составе бортовой системы самолета. Появление теплового разгона приводит к аварийным ситуациям, приводящим к выходу из строя различных блоков радиоэлектронной системы самолета.
Процесс теплового разгона начинается при замыкании электродов. Это приводит к локальному разогреву электродов в месте замыкания до температуры, при которой происходит газовыделение. Затем выделившийся газ начинает гореть. Из-за этого поднимается температура в соседних с точкой замыкания электродов областях. Таким образом, температура электродов описывает как начало теплового разгона, так и процесс его распространения:
![]() , (1)
, (1)
где ![]() ; k - коэффициент теплопроводности; γ - теплоемкость вещества; ρ - плотность вещества;
; k - коэффициент теплопроводности; γ - теплоемкость вещества; ρ - плотность вещества;
![]() . (2)
. (2)
где v(x, y, z, t) - количество тепла, выделяемое в единицу времени из единицы объема электрода. Рассмотрим функцию v(x, y, z, t) . В случае небольших температур количество выделяемого тепла должно быть пропорционально количеству выделяемого газа из электрода. Таким образом, при низких температурах количество выделяемого в каждой точке электрода тепла должно быть возрастающей функцией температуры, т.е.
v = F(T ). (3)
В выражении (3) не должно быть явной зависимости ни от координат, ни от времени, так как только при определенной температуре в любой точке и в любой момент времени начинается газовыделение и, соответственно, начинается реакция горения. То есть количество выделяемого тепла в единицу времени в единице объема v должно зависеть от координат и времени только через температуру.
Когда ресурс реакции исчерпается и выделение тепла прекратится, температура в данной точке электрода достигнет максимального значения, равного значению температуры в предыдущей точке электрода (предполагается, что температура распространяется по радиусу от точки замыкания электродов).
Таким образом, градиент (по радиусу) температуры обратиться в нуль в момент окончания выделения тепла в данной точке. Из аналогичных соображений можно сделать вывод: чем больше разность температур в данной и предыдущей точке, тем больше имеется ресурса для реакции и, следовательно, тем больше будет выделяться тепла.
Отсюда следует, что v должна быть также возрастающей функцией градиента температуры. Таким образом, в общем случае v должна быть возрастающей функцией как температуры, так и градиента температуры в каждой точке электрода.
![]() . (4)
. (4)
Причем
v(T, 0) = 0. (5)
Если воспользоваться экспериментальными данными, представленными в таблице, то получим близкую к линейной зависимость для скорости газовыделения от температуры.
В этом случае формулу (4) необходимо переписать в виде:
![]() . (6)
. (6)
где ![]() мл×мин-1×град-1 - угловой коэффициент линейной.
мл×мин-1×град-1 - угловой коэффициент линейной.
Таблица- Зависимость скорости газовыделения из оксид-никелевого электрода от температуры
|
v, мл/мин |
T, 0C |
|
8,3 |
700 |
|
8,5 |
920 |
|
10,4 |
1000 |
|
12,6 |
1100 |
|
14,5 |
1100 |
В первом приближении, с учетом условия (5), функцию (6) можно представить в виде
![]() . (7)
. (7)
Знак минус в формуле (7) показывает, что только в случае отрицательного градиента происходит выделение тепла. В формуле (7) А - некоторая экспериментальная константа.
В данной модели не учитывается рассеивание тепла в межэлектродное пространство, т.е. учитывать только движение тепла по телу электродов. Это оправдано на первом шаге, так как теплопроводность материала электродов намного выше теплопроводности воды. Следовательно, задача двухмерная. За начало отсчета возьмем точку замыкания электродов. Кроме того считаем, что все свойства электродов изотропны. Таким образом, задача будет симметричной относительно точки замыкания электродов. В соответствии с этим воспользуемся полярной системой координат, тогда уравнение (1) с учетом (7) примет вид [1].
![]() . (8)
. (8)
При достаточно больших значениях R можно пренебречь первым слагаемым справа в уравнении (8), в этом случае получаем стандартное уравнение Бюргерса [2].
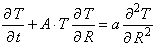 . (9)
. (9)
Найдем решение уравнения (9) при граничных условиях:
![]() (10)
(10)
Получим
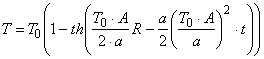 . (11)
. (11)
СПИСОК ЛИТЕРАТУРЫ
- Галушкин Д. Н., Румянцев К. Е., Галушкин Н. Е. Исследование нестационарных процессов в щелочных аккумуляторах: Монография.-Ш.:ЮРГУЭС. -2001.-112с.
- Додд Р., Эйлбек Дж, Гиббон Дж Солитоны и нелинейные волновые уравнения. - М.: Мир. - 1988.-695с.
Библиографическая ссылка
Галушкин Д.Н., Галушкина И.А., Галушкина Н.Н. КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ НЕСТАЦИОНАРНОГО ПРОЦЕССА ТЕПЛОВОГО РАЗГОНА // Фундаментальные исследования. 2005. № 4. С. 61-62;URL: https://fundamental-research.ru/ru/article/view?id=5984 (дата обращения: 16.12.2025).



