Мир вступил в новый, информационный век. Сегодня появляется все больше новых производителей медиаконтента и все больше новых, в том числе технологически инновационных, каналов распространения этого контента. Однако с появлением новых СМИ сам объем медиапотребления не меняется. На практике в основном происходит лишь перераспределение времени и расходов на медиапотребление между растущим числом производителей контента и телевещателями.
В результате происходит дробление аудитории СМИ. Ее становится все сложнее охватить. Именно для решения данной проблемы и возникло медиапланирование как отрасль, призванная находить более эффективные пути донесения информации до аудитории различных медиа [1–3]. Для этого надо использовать различные исследовательские подходы и, в частности, прогнозирование [4].
Цель исследования: анализ основных подходов и разработка методов совершенствования методического инструментария прогнозирования в медиапланировании рейтинга телевизионного контента, выявление возможностей применения адаптивных методов прогнозирования с использованием методов идентификации параметров модели для составления максимально точного прогноза.
Материалы и методы исследования
Исследование просмотра телевизионного и видеоконтента – задача, важность которой интенсивно растет в последнее время. Исследованием объёма и характеристик аудитории СМИ занимается Mediascope – ведущая исследовательская компания на российском рынке в сфере медиаисследований и мониторинга рекламы и СМИ. Mediascope исследует просмотр ТВ-контента на всех платформах – от классического телевизора до digital среды. Одним из преимуществ технологий, применяемых Mediascope в телевизионных исследованиях, является возможность получения социально-демографических характеристик зрителя, для чего каждый участник исследования должен регистрировать вход и выход в помещение с телевизором членов семьи или гостей. Это дает возможность с высокой точностью определять аудиторию конкретных телеканалов и эфирных событий. Полученные данные помогают вещателям показывать наиболее востребованный зрителями контент, а рекламному рынку – планировать, размещать и оценивать рекламные кампании.
На сайте компании [5] представлены основные показатели ведущих телеканалов за последние годы:
– рейтинг телепрограмм – среднее количество человек, смотревших телепрограмму, выраженное в процентах от общей численности исследуемой аудитории;
– доля телепрограммы – среднее количество человек, смотревших телепрограмму, выраженное в процентах от общего количества телезрителей (тех, кто смотрел любую программу, включая оцениваемую программу) в данный момент времени;
– среднесуточная доля телеканала – количество человек, смотревших телеканал в среднем в сутки, выраженное в % от всех телезрителей.
В компаниях-медиаселлерах и рекламных агентствах обычно выполняют прогноз аудитории телевидения по следующей схеме:
1. Считают среднюю долю зрительской аудитории для каждого месяца рассматриваемого периода (обычно год);
2. Далее определяют сезонный коэффициент K для каждого месяца:
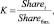
где Sharei – это доля телезрителей за месяц (i = 1: январь, i = 2: февраль и т.д.), а Shareбаз. – это доля зрителей за месяц, который аналитик принимает за базовый. То есть коэффициент сезонности для каждого месяца определяется как отношение размера аудитории в текущий месяц к ее размеру в каком-либо фиксированном месяце.
3. Чтобы построить прогноз, берут значение доли телезрителей за последний известный месяц и умножают на полученные в п. 2 коэффициенты сезонности.
Продемонстрируем это на примере. Пусть нам известны гипотетические помесячные значения доли зрителей канала Х в течение 2018 г. и января 2019 г. (табл. 1). Чтобы спланировать бюджет, необходимо спрогнозировать аудиторию канала на февраль – апрель 2019 г.
Принимаем за базовый месяц январь 2018 г. Значит, коэффициенты сезонности для февраля, марта и апреля будут равны соответственно: K02 = 13/15, K03 = 12/15, K04 = 14/15.
Крайний известный месяц – январь 2019 г. Значит, прогноз на последующие месяцы строится относительно этого месяца.
Share02.19 = К02•Share01.19 = 13/15 • 16 = 13,86,
Share03.19 = К03•Share01.19 = 12/15 • 16 = 12,8,
Share04.19 = К04•Share01.19 = 14/15 • 16 = 14,9.
Считается, что такой прогноз сохраняет наличие сезонных изменений, учитывает отношение аудитории каждого месяца к остальным, а на значение прогнозируемого месяца влияет последний фактический. Как правило, прогнозы строятся на базе данных за 1–2 года, предшествующих прогнозируемому. Считается, что более ранние периоды включают в себя некоторые другие факторы, которые влияли на аудиторию (был другой набор каналов в городе, немного другие предпочтения у людей, другое качество программ и фильмов и т.д.). Тем самым прогноз на базе небольшого набора данных дает более грубую оценку. В итоге это приводит к тому, что прогнозируемое значение, как правило, отличается от зафиксированного позже реального результата.
Предложим другой, более точный метод предварительной оценки и последующего прогноза средней доли телезрителей на некотором канале Y на первые несколько месяцев 2017 г. Выполним анализ по данным Mediascope за 2015–2016 гг. Регион исследования – «Москва», исследуемая аудитория – «население в возрасте от 4 лет и старше». Воспользуемся методом, который объединяет модель авторегрессии и скользящего среднего, которые оказываются особенно эффективными для описания и прогнозирования процессов, обнаруживающих однородные колебания вокруг среднего значения.
Таблица 1
Доля зрителей (Sharei ) канала Х (помесячно январь 2018 г. – январь 2019 г.)
|
Месяц |
01.18 |
02.18 |
03.18 |
04.18 |
05.18 |
06.18 |
07.18 |
08.18 |
|
Sharei |
15 |
13 |
12 |
14 |
15 |
11 |
10 |
11 |
|
Месяц |
09.18 |
10.18 |
11.18 |
12.18 |
01.19 |
02.19 |
03.19 |
04.19 |
|
Sharei |
12 |
13 |
14 |
14 |
16 |
? |
? |
? |
В авторегрессионной модели наиболее сильные связи наблюдаются у соседних состояний и быстро уменьшаются с увеличением расстояния между ними (влияние предыдущего состояния процесса на будущее). Математически это свойство можно выразить уравнением
yt = φ1yt-1 + φ2y t-2 + ...+ φpy t-p + εt,
где уt – значение у в момент времени t; θi – коэффициенты уравнения (i = 1, 2, …, р); р – порядок авторегрессии; εt – случайная величина.
В модели скользящего среднего в отличие от предыдущего способа предполагается, что каждый элемент ряда подвержен суммарному воздействию случайных предыдущих ошибок εi:
yt = θ1 ε t-1 + θ2ε t-2 + ... + θqεt-q + εt,
где уt – значение у в момент времени t; θi – коэффициенты уравнения (i = 1, 2, …, q); q – порядок модели скользящего среднего; εt – случайная величина.
В программе анализа данных Statistica модель, являющаяся комбинацией двух вышеперечисленных, имеет название ARIMA. Данная модель подходит только для стационарных рядов, т.е. для тех, у которых среднее и дисперсия примерно постоянны во времени. Поэтому одним из этапов построения модели (кроме восстановления пропущенных данных, определения порядка модели p и q, оценки параметров модели, проверки адекватности и прогноза) является преобразование ряда к стационарному виду. Возможность реализации этих задач заложена в пакете прикладных программ Statistica [6].
Из рис. 1 видно, что в поведении аудитории наблюдается некоторая сезонная закономерность. В летний период наблюдается сильное уменьшение значения доли зрителей.
Будем строить прогноз исходя из сезонной последовательной зависимости, т.е. учитывать, что на значение доли каждый месяц влияет ее значение в предыдущий месяц. На следующем рисунке представлена автокорреляционная функция, которая показывает, что автокорреляция достигает пиков при лаге, равном 12, что очевидно из соображений сезонности. Но из рис. 2 видно, что корректные результаты также достигаются при сезонном лаге, равном 1, 5, 6 и 7.
Проведем процесс оценивания параметров модели (рис. 3).
На рис. 3 красным цветом выделены наиболее значимые коэффициенты (как правило, это те параметры, которые более чем в два раза превосходят свои стандартные ошибки). Остаточная сумма квадратов и средний квадрат остатков малы, что является подтверждением того, что полученная оценочная модель достаточно близка к фактическим данным.
Прогноз, который выдает программа, строится на период, равный 12 месяцам (рис. 4). Приведем сводку прогнозируемых значений (рис. 5):
Сравнение полученных результатов с фактическими данными за 2017 г. (табл. 2) демонстрирует, что в первые 4 месяца прогноза совпадение происходит с минимальной погрешностью.
Таблица 2
Фактические данные и ошибки прогноза средней доли телезрителей на канале Y за 2017 г.
|
Фактические данные (значения Share) |
Относительные ошибки прогноза |
|
|
Март 2017 |
11,7 |
0,2 % |
|
Апрель 2017 |
11,4 |
1,7 % |
|
Май 2017 |
10,9 |
10 % |
|
Июнь 2017 |
10,3 |
2,9 % |
|
Июль 2017 |
10,1 |
6,9 % |
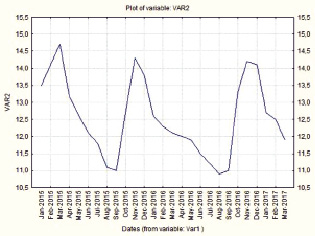
Рис. 1. Значения доли зрителей по месяцам исследуемого периода
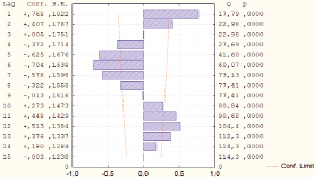
Рис. 2. График автокорреляционной функции
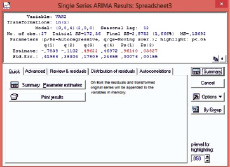
Рис. 3. Результаты расчета коэффициентов и параметров модели
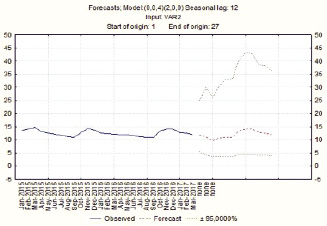
Рис. 4. График прогноза
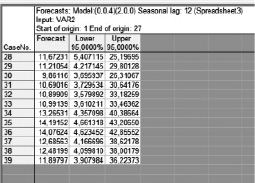
Рис. 5. Прогнозные значения доли зрителей
Результаты исследования и их обсуждение
Адекватность модели была проверена путем построения автокорреляционной функции для остатков. Автокорреляции не выходят за пределы допустимых интервалов, что говорит о независимости остатков. Также было проверено, что остатки распределены по нормальному закону. Выполнение этих двух критериев и подтверждает адекватность полученной модели.
Задача прогнозирования временных рядов имеет высокую актуальность для многих предметных областей и является неотъемлемой частью повседневной работы многих компаний. В настоящее время разработано множество моделей для решения задач прогнозирования временных рядов, среди которых наибольшую применимость имеют авторегрессионные и нейросетевые модели. При этом существенным недостатком авторегрессионных моделей является большое число свободных параметров, требующих идентификации; недостатками нейросетевых моделей является непрозрачность моделирования и сложность обучения сети.
Наиболее перспективным направлением развития моделей прогнозирования с целью повышения точности является создание комбинированных моделей, выполняющих на первом этапе кластеризацию, а затем прогнозирование временного ряда внутри установленного кластера. В ходе исследований было выявлено, что для прогнозирования доли зрителей телеканалов наиболее подходящими оказались методы, которые позволяют объединить модели авторегрессии и скользящего среднего [7, 8]. Применение таких методов является особенно актуальным для описания и прогнозирования процессов, в которых проявляются однородные колебания вокруг среднего значения.
Комбинирование этих методов также эффективно в случае, когда рассматривается ситуация, в которой за промежуток времени, предшествующий прогнозируемому периоду, наблюдается аномальное отклонение данных от обычного поведения (среднего значения для соответствующего месяца). Например, в связи с каким-либо происшествием закрывается показ рекламы в эфире, что влечет резкий нехарактерный спад рейтинга в данном месяце. В таком случае в алгоритме построения прогноза добавляется пункт сглаживания отклонения, который должен производиться без нарушения общих тенденций поведения аудитории на всем периоде.
Заключение
В составлении прогнозов в сфере рекламы есть еще много моментов, требующих глубокого математического анализа [9]. Построение прогнозов с учетом максимального количества факторов и особенностей, таких как конкуренция и сезонность, может быть реализовано с использованием адаптивных методов прогнозирования. При таком подходе особый интерес представляет использование методов идентификации параметров модели для составления максимально точного прогноза [10]. Данная составляющая часть процесса моделирования нередко игнорируется, и производится оценка параметров стандартными приемами, что зачастую снижает точность прогноза. Применение комбинированных моделей является направлением, которое при корректном подходе позволяет повысить точность прогнозирования. Главным недостатком комбинированных моделей является сложность и ресурсоемкость их разработки: нужно разработать модели таким образом, чтобы компенсировать недостатки каждой из них, не потеряв достоинств. Поэтому требуется продолжение исследований в указанном направлении.
Библиографическая ссылка
Полежаев В.Д., Юсупова К.О. ПРОГНОЗИРОВАНИЕ РЕЙТИНГА ТЕЛЕВИЗИОННЫХ КАНАЛОВ НА ОСНОВЕ ДАННЫХ МЕДИАИССЛЕДОВАНИЙ // Фундаментальные исследования. 2019. № 5. С. 99-104;URL: https://fundamental-research.ru/ru/article/view?id=42467 (дата обращения: 14.01.2026).



