Прогнозирование в финансах и экономике в современности предполагает применение разнообразных эконометрических моделей, основанных на экономико-математических методах и их принципах. Использование различных IT-технологий, анализа больших данных в совокупности с разработанными эконометрическими методами даёт большие перспективы для усовершенствования методов в прогнозировании и увеличении эффективности от этого.
В наши дни одной из основных моделей для получения прогнозов по временным рядам в финансово-экономической сфере является модель векторной авторегрессии и её существующие модификации. Применение таких векторных авторегрессий в анализе финансовых показателей является главным следствием различного вида критики активно применявшихся прежде эконометрических моделей традиционного типа. Модель векторной авторегрессии (сокращённо VAR – Vector Autoregressive Model), во-первых, представляется как обобщение AR-моделей в случае применения многомерных временных рядов. А во-вторых, VAR-модель представляет собой частный случай системы, состоящей из одновременных уравнений. В середине 1980-х гг. она была разработана величайшим исследователем Кристофером Симсом в качестве альтернативы системам, состоящим из одновременных уравнений и предполагающим серьёзные ограничения в части теории. В VAR-моделях не делаются попытки воспроизвести реальную существующую экономическую структуру, в них также не выявляются различия между зависимыми (эндогенными) и определяющими (экзогенными) переменными. Каждое из отдельно взятых уравнений рассматриваемой модели предполагает функциональную зависимость одной из эндогенных переменных модели от лаговых значений по всем имеющимся переменным в модели.
Модели данной спецификации широко распространены как в структурном анализе, так и в прогнозировании благодаря своей относительной простоте и логичности. Но для правильного отображения динамики фактических данных временных рядов, VAR-модели часто потребуются лаги в большом количестве, что способно привести к большим ошибкам в полученных прогнозах. Применение VAR-моделей с высокой размерностью потенциально способно сделать более корректным качество прогноза [1]. Однако в данном случае увеличение количества переменных в векторной авторегрессии может привести к такому случаю, когда количество параметров в оценке будет расти в нелинейном представлении. Переменные, которые позволяют моделировать своё поведение в определённом промежутке времени, в рамках VAR формируют многомерный временной ряд данных. Часто высказываются предположения о том, что данные ряды, которые представляют собой вектор некоторых переменных, генерирует некий стохастический процесс. Таким образом, модель VAR описывает некое совместное развитие переменных за выбранный период времени, опираясь на ряд информации, содержащейся в самих исследуемых временных рядах. Скорее, одно из самых простых определений, которое получится дать VAR-модели, следующее: это некоторая модель эконометрики, одновременно описывающая действия совместно зависимых переменных через изменение своих значений предшествующих периодов и значений других совместно зависимых переменных.
В наше время ценности точных прогнозов очень тяжело дать завышенную оценку. Структура, основанная на лаговых переменных, в большинстве процессов финансов и экономики может приводить к ситуации, когда решения, принимающиеся сегодня, будут существенно влиять на часть результатов будущего периода, поэтому при выборе решения стоит ориентироваться также на ожидаемые показатели, а не только на текущие. Увеличение точности и адекватности полученных прогнозов по показателям в финансово-экономической сфере входит в число ключевых задач в исследованиях по принятию оптимальных решений. Значит, целью, которая ставится в данном исследовании, можно назвать обзор известных методов построения VAR-моделей и их практическое применение в финансах и экономике.
Результаты исследования и их обсуждение
К самому простому случаю векторной авторегрессии можно отнести рассмотрение поведения двух переменных. Значит, такая модель будет учитывать AR-составляющие 1-го порядка. Обозначим переменные модели, которые являются совместно зависимыми, как Xt и Yt, где t – номер периода времени. Если учитывать главные предположения спецификации, то модель будет содержать два уравнения. В каждое из этих двух рассматриваемых уравнений (как для Xt, так и для Yt) будут входить AR-составляющие 1-го порядка Xt-1 и Yt-1. Таким образом, мы получаем такую систему уравнений, которую в данных обстоятельствах правильным будет назвать моделью VAR 1-го порядка [2]:
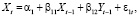 (1.1)
(1.1)
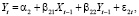 (1.2)
(1.2)
где α1, β11, β12, α2, β21, β22 – оцениваемые параметры модели.
Индекс параметров, который находится на первом месте, ссылается на уравнение, а второй индекс – на порядковый номер переменной. То есть, например, индексы у β21 показывают на то, что параметр является составной частью второго уравнения, а также находится при значениях переменной Xt-1. Случайные остатки в моделях для рассматриваемых уравнений обозначены как ε1t и ε2t соответственно и являются процессами белого шума, имеющими следующие параметры распределения:
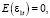
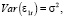 (1.3)
(1.3)
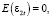
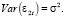 (1.4)
(1.4)
Предположим, что случайные остатки ε1t и ε2t не будут коррелировать друг с другом независимо от Xt и Yt, однако в общих случаях данные процессы могут между собой и коррелировать. Также отметим, что от распределения зависимых переменных Xt и Yt не зависит распределение случайных остатков ε1t и ε2t .
В VAR-моделях интерпретация оцениваемых параметров определяется структурой построенных уравнений. Например, значение β11, отличное от нуля, свидетельствует об имеющихся процессах автокорреляции в Xt, а значение β12, отличное от нуля, будет означать то, что значения переменной Yt-1 оказывают существенное влияние на процесс, в котором заложено формирование Xt [3]. Похожее определение в отношении процесса, который представлен в Yt, имеют β21 и β22, а также константы α1 и α2.
Исходную систему уравнений (1.1)–(1.2) можно записать в матричном виде и ввести соответствующие обозначения:
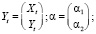
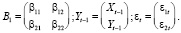 (1.5)
(1.5)
Следовательно, с учётом (1.5) VAR-модель примет следующий вид:
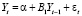 , (1.6)
, (1.6)
которую следует определять как VAR(1).
Введённые замены позволят обобщать матричную запись VAR-модели 1-го порядка VAR(1) на случай AR более высокого порядка, а также при увеличении размерности [4]. Обозначим как p – порядок AR, k – число совместно зависимых переменных, где k будет определять размерность вектора Yt. При данных обозначениях вектор будет включать k переменных, являющихся совместно зависимыми:
Yt = (Y1t, Y2t, ..., Ykt)T.
Кроме того, введём векторы отставания значений совместно зависимых переменных Yt-1, Yt-2, ..., Yt-p соответственно с лагом запаздывания 1, 2,…, p; размерность векторов Yt-1, Yt-2, ..., Yt-p равна значению k. Введём обозначение α как вектора параметров констант в уравнениях (размерность равна k); B1, B2,…, Bp – матрицы параметров (размерность равна k×k), соответствующие векторам переменных Yt-1, Yt-2, ..., Yt-p соответственно:
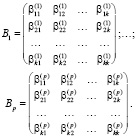
Вектор случайных остатков εt также имеет размерность k:
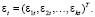
Распределение членов вектора εt можно охарактеризовать как процесс белого шума:
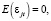
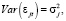
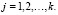
Введём обозначение ковариационной матрицы возмущений ε1t, ε2t,…, εkt – для каждого периода времени t как E (размерность равна k×k). В случае истинности предположения о некоррелированности случайных остатков матрица E принимает диагональный вид с элементами 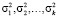 , которые располагаются на главной диагонали.
, которые располагаются на главной диагонали.
В данном случае VAR-модель порядка p, которую обычно обозначают как VAR(p), можно записать следующим образом:
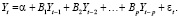 (1.7)
(1.7)
Любые системы уравнений принято выделять как в структурной, так и в приведённой форме. Запись VAR в форме (1.1)–(1.2) или в (1.7) необходимо рассматривать как аналог приведённой формы, так как совместно зависимые переменные не используются в правой части уравнений в качестве объясняющих переменных. Коэффициенты α, B1, B2,…, Bp в (1.7) являются приведёнными. Сравнивая с системами одновременных уравнений, отметим, что все переменные в VAR-модели Y1t, Y2t, ..., Ykt, которые характеризуют состояние процессов на текущий момент, будут играть роль переменных, являющихся совместно зависимыми. Запаздывающие переменные Yt-1, Yt-2, ..., Yt-p выступают как предопределённые и функционируют для объяснения динамики зависимых переменных. Отметим, что в VAR все переменные будут определяться внутри самой системы, то есть будут являться объясняемыми (эндогенными). Также наличие запаздывающих переменных Yt-1, Yt-2, ..., Yt-p позволяет классифицировать построенную модель (1.7) как динамическую.
Система уравнений (1.7) представляет собой исходный или традиционный вариант модели векторной авторегрессии [5]. В традиционном варианте модели нет экзогенных переменных, они не выступают в роли объясняющих переменных. Также не выступают в роли объясняющих переменных и Y1t, Y2t, ..., Ykt, являющиеся совместно зависимыми. Поведение всех таких переменных объясняется через влияние с запаздыванием со стороны самих эндогенных переменных Y1t, Y2t, ..., Ykt. Важно понимать эту особенность векторной авторегрессии. Тем не менее модель допускает включение экзогенных переменных в качестве объясняющих. Это может быть сделано, например, следующим образом. Пусть Xt = (X1t, X2t, ..., Xqt)T – вектор текущих или предшествующих моменту t значений объясняющих переменных, где всего имеется q переменных; C – матрица параметров (размерность равна k×q), соответствующая вектору экзогенных переменных [6]:

Тогда VAR-модель с экзогенными переменными примет следующий вид:
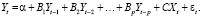
В качестве экзогенной переменной может выступать, например, переменная времени t, отражающая при необходимости временной тренд.
Н. Маматова в своей статье «Применение модели векторной авторегрессии для анализа потребления электроэнергии» предложила следующую модель VAR [7]:
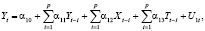
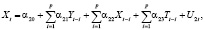
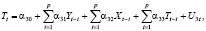
где Y – потребление электроэнергии,
X – производство электроэнергии,
T – тарифы на электроэнергию
αij – коэффициенты, которые подлежат оцениванию.
В итоге анализа VAR-модели автором было найдено, что на уровень потребления электроэнергии существенно влияет повышение тарифов за электроэнергию.
Т.А. Белова, Р.Х. Бахитова в своём исследовании «Эконометрическая модель диагностики и прогнозирования отраслей экономики г. Уфы» построили модель, которая служит для диагностики и прогнозирования экономики города на основе VAR-модели [8]. Построенные модели прогнозирования и диагностики экономики Уфы дали очень качественную оценку экономической ситуации системы города, а также позволили предсказать тренд развития на будущую перспективу, смогли выявить преимущества над конкурентами и проблемы функционирования экономической системы современного мегаполиса. Полученная исследователями информация является очень полезной для органов государственной власти в решении спорных вопросов, связанных с улучшением уровня и качества жизни горожан, ростом благосостояния населения, развитием инфраструктуры, эффективном процветании города в социально-экономической сфере, развитием конкурентоспособной экономики, расширением внешних связей.
Е.И. Суханова, С.Ю. Ширнаева в своей работе «Прогнозирование показателей стабилизационных процессов экономики России на основе моделей векторной авторегрессии» получили результаты построения и использования моделей VAR для прогнозирования значений показателей в краткосрочном периоде. Авторы отражают стабилизационные процессы, которые протекают в российской экономике, а также сравнивают точности прогнозов, полученных с помощью VAR-моделей, с прогнозами на основе системы одновременных уравнений (СОУ) [9]. Проведённое исследование позволило им сделать вывод о том, что модели VAR – достаточно эффективный, простой и менее трудоемкий инструмент для прогнозирования значений различных экономических показателей, отражающих процессы, протекающие в российской экономике.
Если учесть разнообразие объясняющих переменных, сезонных составляющих и трендов в финансах и экономике, то можно сделать вывод о том, что VAR-модели абсолютно применимы для прогнозирования ключевых макро- и микроэкономических показателей. Универсальность и простота применения моделей векторной авторегрессии является одним из основных её преимуществ, которые следует учитывать при выборе инструмента анализа и прогнозирования в финансово-экономической сфере.
Заключение
Модели векторной авторегрессии широко используются как для прогнозирования, так и для структурного анализа в абсолютно различных местах – от частных промышленных предприятий до государственных структур. Использование данных моделей помогает улучшать качество прогноза интересующих показателей. Представленное исследование посвящено механизму построения моделей векторных авторегрессий и их применению для построения прогнозов в финансах и экономике на основании традиционных подходов.
Библиографическая ссылка
Каменский Д.А. ПРИМЕНЕНИЕ МОДЕЛЕЙ ВЕКТОРНОЙ АВТОРЕГРЕССИИ ПРИ ПРОГНОЗИРОВАНИИ В ФИНАНСАХ И ЭКОНОМИКЕ // Фундаментальные исследования. 2019. № 5. С. 45-49;URL: https://fundamental-research.ru/ru/article/view?id=42459 (дата обращения: 17.11.2025).



