Проблематика управления портфелем финансовых активов неиституционального инвестора – агента российского фондового рынка в разное время рассматривалась многими российскими исследователями, в частности Н.Е. Егоровой, А.В. Мищенко, И.А. Киселевой и др., а из последних работ на эту тему выделим работы Д.А. Быстровой и М.А. Рязанова [1], М.А. Халикова и Д.А. Максимова [2]. В этих и других работах рассматривается задача оптимизации финансового портфеля неинституционального инвестора, однако в «упрощённом» варианте, без учета динамических характеристик портфеля и в непрерывной постановке, что не соответствует реалиям современного фондового рынка.
В связи с этим отметим, что широко известные модели портфельных инвестиций Г. Марковица, У. Шарпа, Дж. Тобина [3] имеют ограниченное применение для развивающегося финансовых рынков и, в частности, для российского, по следующим причинам:
– рынок высоко изменчив. На сегодняшний день волатильность составляет 28,9 % (рис. 1) [4];
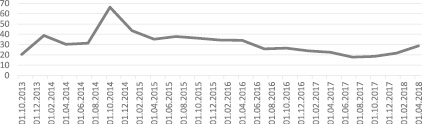
Рис. 1. Российский индекс волатильности RTSVX, группа «Московская биржа»
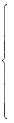
Рис. 2. Блок-схема алгоритма динамической модели оптимизации финансового портфеля на k-й торговой площадке (начало рисунка)
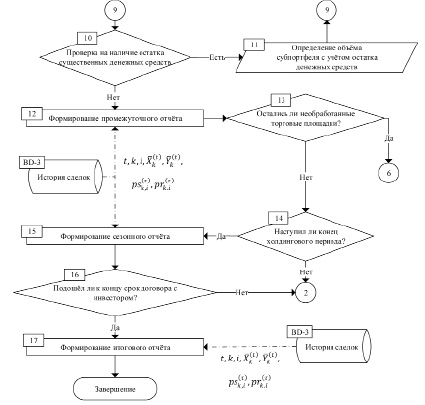
Рис. 2. Блок-схема алгоритма динамической модели оптимизации финансового портфеля на k-й торговой площадке (окончание рисунка)
– с рынка уходят крупные инвесторы [5], а средние и мелкие при принятии инвестиционных решений оперируют расширенным набором критериев качества, включающим наряду с риском, доходностью и ликвидность финансовых активов.
Цель исследования: учитывая эти и некоторые другие институциональные особенности и неинституциональные отличия российского фондового рынка (например, низкую эффективность рынка и дискретность торгуемых лотов), целью настоящей работы является разработка математической модели и информационно-алгоритмического обеспечения динамической оптимизации портфеля финансовых активов неинституциольного инвестора, реализующих следующие идеи:
1) постоянный мониторинг (повторяющийся с периодичностью торговых сессий) финансовых активов, которые либо включены в портфель инвестора, либо находятся в его «резерве» для расширения потенциального списка активов инвестирования, которые ранее не удовлетворяли предпочтениям инвестора по критериям доходность – риск – ликвидность, а с какого-то момента времени становятся объектом инвестирования [6];
2) оперирование не только интегральной ценой купли-продажи финансового актива, как это принято в «традиционной» портфельной теории, а с выделением двух рядов цен, наблюдаемых инвестором для указанных активов: цены продажи и цены покупки, что крайне важно для низколиквидных фондовых рынков [7];
3) управление портфелем на двух уровнях (на верхнем – управляющая компания, на нижнем – торговая площадка и оперирующий на ней брокер), что позволяет повысить качество инвестиционного решения за счет перераспределения информации по уровням принимаемого решения критериев доходности и системы ограничений.
Материалы и методы исследования
Используемый в работе научно-методический и теоретический материал включает авторские и цитируемые работы других авторов по проблематике фондовых рынков, финансовых операций и математико-экономического инструментария управления финансовыми портфелями [8–10].
Результаты исследования и их обсуждение
Для управления инвестиционным портфелем неинституционального инвестора на k-й торговой площадке 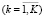 воспользуемся динамической моделью, состоящей из двух уровней.
воспользуемся динамической моделью, состоящей из двух уровней.
Цель задачи верхнего уровня – максимизация совокупного эффекта распределения денежных средств УК между торговыми площадками.
Цель задачи нижнего уровня – определение плана покупки ценных бумаг и предполагаемой доходности портфеля с учетом риска.
Оценкой эффективности управления инвестиционным портфелем неинституционального инвестора на k-й торговой площадке на верхнем уровне является дисконтированный поток чистых доходов:
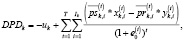 (1)
(1)
где I,i1,i2 – индексы ценных бумаг, обращающихся на k-й торговой площадке (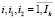 );
);
t, τ – индексы временных интервалов 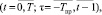 где T – плановый горизонт, Тпр – предшествующий нулевому горизонт мониторинга k-й торговой площадки;
где T – плановый горизонт, Тпр – предшествующий нулевому горизонт мониторинга k-й торговой площадки;
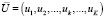 – вектор распределения денежных средств между торговыми площадками;
– вектор распределения денежных средств между торговыми площадками;
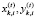 – величины соответственно продаваемого и покупаемого на k-й торговой площадке на временном интервале t i-го актива (
– величины соответственно продаваемого и покупаемого на k-й торговой площадке на временном интервале t i-го актива (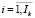 );
);
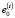 – ставка дисконтирования для периода t, совпадающая с доходностью в этом периоде среднерыночного портфеля;
– ставка дисконтирования для периода t, совпадающая с доходностью в этом периоде среднерыночного портфеля;
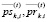 – средние за период [
– средние за период [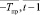 ] соответственно цены продажи, покупки i-го актива, обращающегося на k-й торговой площадке:
] соответственно цены продажи, покупки i-го актива, обращающегося на k-й торговой площадке:
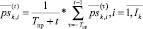 ; (2)
; (2)
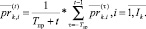 (3)
(3)
В дальнейшем для единообразия понятия будем оперировать термином k-й субпортфель, имея в виду портфель финансовых активов неинституционального инвестора, включающий ценные бумаги, операции с которыми осуществляются на k-й торговой площадке.
На верхнем уровне решается задача распределения инвестиционных ресурсов между площадками:
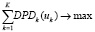 ; (4)
; (4)
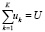 ; (5)
; (5)
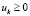 ,
, 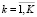 . (6)
. (6)
Задача нижнего уровня состоит из двух этапов. На первом этапе осуществляется поиск решения «классической» задачи Г. Морковица (в непрерывной постановке).
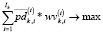 ; (7)
; (7)
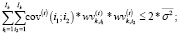 (8)
(8)
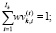 (9)
(9)
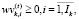 (10)
(10)
где 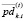 – средняя за период [
– средняя за период [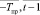 ] доходность i-го актива, обращающегося на k-й торговой площадке:
] доходность i-го актива, обращающегося на k-й торговой площадке:
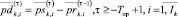 ; (11)
; (11)
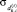 – среднеквадратическое отклонение от среднего значения, полученного за период наблюдения [–Tпр, t – 1], доходности i-го актива на k-й торговой площадке:
– среднеквадратическое отклонение от среднего значения, полученного за период наблюдения [–Tпр, t – 1], доходности i-го актива на k-й торговой площадке:
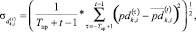
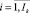 ; (12)
; (12)
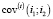 – элементы прямоугольной матрицы коэффициентов ковариации доходностей финансовых активов с индексами i1 и i2, рассчитанных на основе наблюдаемых значений доходностей составляющих k-го субпортфеля на промежутке [–Tпр, t – 1],
– элементы прямоугольной матрицы коэффициентов ковариации доходностей финансовых активов с индексами i1 и i2, рассчитанных на основе наблюдаемых значений доходностей составляющих k-го субпортфеля на промежутке [–Tпр, t – 1], 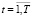 :
:
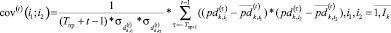 ; (13)
; (13)
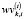 – доля i-го актива в совокупном инвестиционном портфеле к концу временного интервала t,
– доля i-го актива в совокупном инвестиционном портфеле к концу временного интервала t, 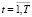 :
:
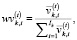 (14)
(14)
где 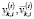 – объемы i-го актива, находящиеся в управлении брокера k-й торговой площадки соответственно в начале и конце временного интервала t (t ≥ 1):
– объемы i-го актива, находящиеся в управлении брокера k-й торговой площадки соответственно в начале и конце временного интервала t (t ≥ 1):
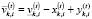 ,
, 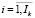 ;
; 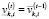 ,
, 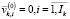 . (15)
. (15)
Задача (7)–(10), в силу ограничения (8) относится к задачам нелинейного (в данном случае, выпуклого программирования) с линейным функционалом (7), что обеспечивает единственность оптимального решения, совпадающего с экстремумом соответствующей функции Лагранжа:
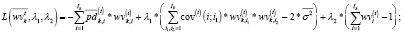 (16)
(16)
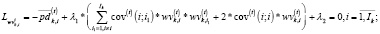 (17)
(17)
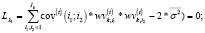 (18)
(18)
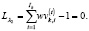 (19)
(19)
Численный алгоритм решения задачи (7)–(10) может быть основан на градиентном методе. При этом начальным приближением может служить оптимальный k-й субпортфель, полученный на шаге t – 1.
На втором этапе осуществляется выбор оптимального по критерию доходности операций с инвестиционным портфелем неинституционального инвестора на k-й торговой площадке план продажи-покупки финансовых активов. Используется следующая дискретная оптимизационная модель:
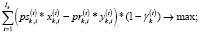 (20)
(20)
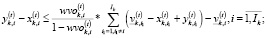 (21)
(21)
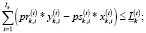 (22)
(22)
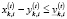 ,
, 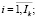 (23)
(23)
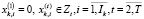 ; (24)
; (24)
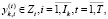 (25)
(25)
где 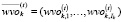 – вектор с компонентами, определяющими оптимальную структуру k-го субпортфеля на временном интервале t.
– вектор с компонентами, определяющими оптимальную структуру k-го субпортфеля на временном интервале t.
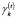 – доля трансакционных и операционных затрат в общем объеме затрат по управлению инвестиционным портфелем на k-й торговой площадке на временном интервале t;
– доля трансакционных и операционных затрат в общем объеме затрат по управлению инвестиционным портфелем на k-й торговой площадке на временном интервале t;
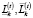 – объемы свободных для инвестирования в финансовые активы на k-й торговой площадке денежных средств соответственно в начале и в конце временного интервала t:
– объемы свободных для инвестирования в финансовые активы на k-й торговой площадке денежных средств соответственно в начале и в конце временного интервала t:
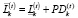 ,
, 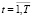 ; (26)
; (26)
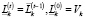 , (27)
, (27)
где Vk – объем инвестиций, предоставленных УК k-й торговой площадки в стартовом временном интервале;
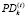 – ожидаемая доходность операций с инвестиционным портфелем на k-й торговой площадке на временном интервале t (t ≥ 1);
– ожидаемая доходность операций с инвестиционным портфелем на k-й торговой площадке на временном интервале t (t ≥ 1);
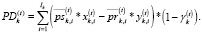 (28)
(28)
Остановимся на ограничении (22), задающем бюджет «дискретного портфеля». Этот бюджет рассчитывается с учетом нераспределенного остатка средств, отличающих непрерывный портфель от целочисленного [11–12]. Объем дополнительно учитываемых при формировании дискретного портфеля средств зависит от первоначального бюджета инвестора (чем больше первоначальный бюджет, тем в меньшей степени этот остаток значим для инвестора), предпочтений инвестора (в случае, если его интересуют «дорогие активы», то фактор величины остатков значим и наоборот) [13]. В любом случае, значимость величины остатка бюджета, учитываемого при формирования дискретного портфеля, должна определяться в договоре с управляющей компанией.
Задача (20)–(25) относится к задачам линейного целочисленного программирования и эффективно решается с использованием известных методов дискретной оптимизации, например, метода «ветвей и границ», либо предложенного в работе [14] метода локальной оптимизации поиска квазиоптимального решения задачи дискретного программирования.
Для практической реализации динамической модели управления портфелем финансовых активов неинституционального инвестора на последовательности временных интервалах, составляющих единый холдинговый период, и ее верификации в управлении портфелем выбранного инвестора нами разработано информационно-алгоритмическое обеспечение, включающее численный алгоритм (ниже приведена блок-схема этого алгоритма и программный модуль, реализованный с использованием языка программирования JavaScript и технологий Node.js и Electron).
Комментарии к блок-схеме:
1. Заключение договора с неинституциональным инвестором на предоставление услуг управления инвестиционного портфеля. Внесение брокером в программу срока действия договора и размера денежных инвестиций.
2. Актуализация базы данных (БД) ценных бумаг, расчёт показателей ценных бумаг:
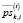 – средней за период [–Tпр, t – 1] цены продажи i-го актива, обращающегося на k-й торговой площадке;
– средней за период [–Tпр, t – 1] цены продажи i-го актива, обращающегося на k-й торговой площадке;
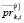 – средней за период [–Tпр, t – 1] цены покупки i-го актива, обращающегося на k-й торговой площадке;
– средней за период [–Tпр, t – 1] цены покупки i-го актива, обращающегося на k-й торговой площадке;
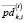 – средней за период [–Tпр, t – 1] доходности i-го актива, обращающегося на k-й торговой площадке;
– средней за период [–Tпр, t – 1] доходности i-го актива, обращающегося на k-й торговой площадке;
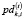 – доходности i-го актива, обращающегося на k-й торговой площадке;
– доходности i-го актива, обращающегося на k-й торговой площадке;
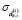 – среднеквадратического отклонения от среднего значения, полученного за период наблюдения [–Tпр, t – 1], доходности i-го актива на k-й торговой площадке;
– среднеквадратического отклонения от среднего значения, полученного за период наблюдения [–Tпр, t – 1], доходности i-го актива на k-й торговой площадке;
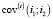 – элементов прямоугольной матрицы коэффициентов ковариации доходностей финансовых активов с индексами i1 и i2, рассчитанных на основе наблюдаемых значений доходностей составляющих k-го субпортфеля на промежутке [–Tпр, t – 1],
– элементов прямоугольной матрицы коэффициентов ковариации доходностей финансовых активов с индексами i1 и i2, рассчитанных на основе наблюдаемых значений доходностей составляющих k-го субпортфеля на промежутке [–Tпр, t – 1], 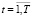 .
.
3. Проводится проверка наступления нового холдингового периода на начало текущей рабочей сессии. При положительной проверки требуется сформировать новый производственный календарь для нового холдингового периода и распределить денежные средства инвестора между торговыми площадками.
4. Формирование рабочего календаря на текущий холдинговый период: определение границ холдингового периода (месяц, квартал, полугодие, произвольно) и конкретизация торговых дней работы торгового агента, брокера, с учётом сроков договора.
5. Задача верхнего уровня: распределение денежных средств между торговыми площадками.
Входная информация:
U – объем инвестиций, предоставленных УК стартовом временном интервале;
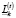 – объем свободных для инвестирования в финансовые активы денежных средств соответственно в начале временного интервала t;
– объем свободных для инвестирования в финансовые активы денежных средств соответственно в начале временного интервала t;
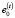 – ставка дисконтирования для периода t, совпадающая с доходностью в этом периоде среднерыночного портфеля;
– ставка дисконтирования для периода t, совпадающая с доходностью в этом периоде среднерыночного портфеля;
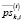 – средняя за период [–Tпр, t – 1] цена продажи i-го актива, обращающегося на k-й торговой площадке;
– средняя за период [–Tпр, t – 1] цена продажи i-го актива, обращающегося на k-й торговой площадке;
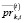 – средняя за период [–Tпр, t – 1] цена покупки i-го актива, обращающегося на k-й торговой площадке;
– средняя за период [–Tпр, t – 1] цена покупки i-го актива, обращающегося на k-й торговой площадке;
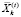 – вектор объёмов i-го актива, продаваемых на k-й торговой площадке на временном интервале t;
– вектор объёмов i-го актива, продаваемых на k-й торговой площадке на временном интервале t;
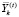 – вектор объёмов i-го актива, покупаемых на k-й торговой площадке на временном интервале t.
– вектор объёмов i-го актива, покупаемых на k-й торговой площадке на временном интервале t.
Выходная информация:
uk – объем инвестиций, предоставленных УК k-й торговой площадки в стартовом временном интервале;
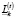 – объемы свободных для инвестирования в финансовые активы на k-й торговой площадке денежных средств в начале временного интервала t.
– объемы свободных для инвестирования в финансовые активы на k-й торговой площадке денежных средств в начале временного интервала t.
6. Выбор торговой площадки для последующей коррекции инвестиционного портфеля и его показателей. Организуется путём идентификации ЛПР (лица, принимающего решения, брокер) k-й торговой площадки и соответствующее субпортфелю.
7. Проверка текущего статуса рынка на наличие непредвиденных обстоятельств, из-за которых временно приостанавливается работа брокеров на бирже.
8. Задача нижнего уровня – 1 этап: расчёт оптимальной структуры субпортфелей с учётом риска.
Входная информация:
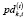 – доходность i-го актива, обращающегося на k-й торговой площадке;
– доходность i-го актива, обращающегося на k-й торговой площадке;
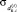 – среднеквадратическое отклонение от среднего значения, полученного за период наблюдения [–Tпр, t – 1], доходности i-го актива на k-й торговой площадке;
– среднеквадратическое отклонение от среднего значения, полученного за период наблюдения [–Tпр, t – 1], доходности i-го актива на k-й торговой площадке;
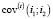 – элементы прямоугольной матрицы коэффициентов ковариации доходностей финансовых активов с индексами i1 и i2, рассчитанных на основе наблюдаемых значений доходностей составляющих -го субпортфеля на промежутке [–Tпр, t – 1],
– элементы прямоугольной матрицы коэффициентов ковариации доходностей финансовых активов с индексами i1 и i2, рассчитанных на основе наблюдаемых значений доходностей составляющих -го субпортфеля на промежутке [–Tпр, t – 1], 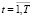 .
.
Выходная информация:
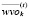 – вектор с компонентами, определяющими оптимальную структуру k-го субпортфеля на временном интервале t.
– вектор с компонентами, определяющими оптимальную структуру k-го субпортфеля на временном интервале t.
9. Задача нижнего уровня – 2 этап: расчёт объёма покупки и продажи финансовых активов.
Входная информация:
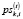 – цены продажи i-го актива, обращающегося на k-й торговой площадке;
– цены продажи i-го актива, обращающегося на k-й торговой площадке;
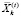 – вектор объёмов i-го актива, продаваемых на k-й торговой площадке на временном интервале t;
– вектор объёмов i-го актива, продаваемых на k-й торговой площадке на временном интервале t;
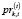 – цена покупки i-го актива, обращающегося на k-й торговой площадке;
– цена покупки i-го актива, обращающегося на k-й торговой площадке;
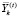 – вектор объёмов i-го актива, покупаемых на k-й торговой площадке на временном интервале t;
– вектор объёмов i-го актива, покупаемых на k-й торговой площадке на временном интервале t;
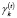 – доля трансакционных и операционных затрат в общем объеме затрат по управлению инвестиционным портфелем на k-й торговой площадке на временном интервале t;
– доля трансакционных и операционных затрат в общем объеме затрат по управлению инвестиционным портфелем на k-й торговой площадке на временном интервале t;
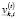 – объем i-го актива, находящегося в управлении брокера k-й торговой площадки в начале временного интервала t;
– объем i-го актива, находящегося в управлении брокера k-й торговой площадки в начале временного интервала t;
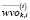 – вектор с компонентами, определяющими оптимальную структуру k-го субпортфеля на временном интервале t;
– вектор с компонентами, определяющими оптимальную структуру k-го субпортфеля на временном интервале t;
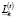 – объемы свободных для инвестирования в финансовые активы на k-й торговой площадке денежных средств в начале временного интервала t.
– объемы свободных для инвестирования в финансовые активы на k-й торговой площадке денежных средств в начале временного интервала t.
Выходная информация:
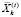 – вектор объёмов i-го актива, продаваемых на k-й торговой площадке на временном интервале t;
– вектор объёмов i-го актива, продаваемых на k-й торговой площадке на временном интервале t;
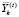 – вектор объёмов i-го актива, покупаемых на k-й торговой площадке на временном интервале t.
– вектор объёмов i-го актива, покупаемых на k-й торговой площадке на временном интервале t.
10. Проверка наличия существенных остатков денежных средств (в соответствии с предпочтениями УК и инвестора) для k-й торговой площадки по результатам решения задачи нижнего уровня второго этапа.
11. Определение объёма субпортфеля с учётом остатка денежных средств.
12. Формирование промежуточного отчёта для k-й торговой площадки текущей, отражающего текущую рабочую сессию брокера. Если сессия не состоялась, то отчёт будет сформирован автоматически.
13. Выбор очередной торговой площадки и соответствующего субпортфеля. Если все торговый площадки «отработаны», то переход на пункт № 6.
14. Проверка окончания холдингового периода на конец текущей рабочей сессии. Если наступил, то переход в пункт № 15 для формирования сезонного отчёта, иначе возврат в пункт № 2 для начала новой рабочей сессии.
15. Формирование сезонного отчёта по итогам конца холдингового периода. При пропуске данного шага отчёт будет сформирован автоматически. Переход на новый холдинговый период.
16. Проверка срока окончания договора инвестором. Если срок договора закончился, то переход в пункт № 17 для формирования итогового отчёта, иначе возврат в пункт № 2 для начала новой рабочей сессии.
17. Формирование итогового отчёта по всем торговым площадкам.
Заключение
Эмпирические расчеты по представленной выше математической модели динамической оптимизации портфеля финансовых активов неинституционального инвестора проведены с финансовым портфелем ООО «ЭликСи-мед», которое по инвестиционным предпочтениям и объему инвестиционного капитала можно отнести к умеренно-агрессивному долгосрочному инвестору, на временном интервале сентябрь 2017 – апрель 2018 гг. Эти результаты продемонстрировали корректность предложенных моделей и численных алгоритмов и их высокую адаптивность к изменениям параметров рынка, учитываемых в предпочтениях этого инвестора. Важной, однако, является адаптация алгоритма динамической модели и для других групп неинституциональных инвесторов, отличающихся сроками инвестирования, отношением к риску – доходности – ликвидности и величиной инвестиционного бюджета.
Авторы выражают благодарность д.э.н., проф. М.А. Халикову за содействие при подготовке данной работы.
Библиографическая ссылка
Быстрова Д.А., Зинчук М.Г., Лошаков М.А. МАТЕМАТИЧЕСКИЕ МОДЕЛИ И ИНФОРМАЦИОННО-АЛГОРИТМИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ДИНАМИЧЕСКОЙ ОПТИМИЗАЦИИ ПОРТФЕЛЯ ФИНАНСОВЫХ АКТИВОВ НЕИНСТИТУЦИОНАЛЬНОГО ИНВЕСТОРА // Фундаментальные исследования. 2018. № 8. С. 17-25;URL: https://fundamental-research.ru/ru/article/view?id=42232 (дата обращения: 15.01.2026).



