Поиск пути является нетривиальной математической задачей нахождения оптимального маршрута между двумя точками алгоритмическим методом. Практическое применение решения задачи используется при моделировании различных процессов или недетерминированных машин, при работе картографических сервисов, при расчете стоимости построения дорог через сложную местность, при выборе пути робота как часть системы машинного зрения [1].
Введение неоднородности среды и использование недискретизированного рабочего пространства является одним из вариантов приближения задачи к реальной картине. При этом значительно возрастает расчетное время. Особенностью работы является применение генетических алгоритмов при решении задачи.
Основной целью статьи является описание задачи, алгоритма ее решения и демонстрация его работы на пробном рабочем поле.
Постановка задачи
На рабочем пространстве расположены начало и конец пути, а также множество зон произвольной формы, имеющие весовые коэффициенты k, обозначающие изменение стоимости прокладки пути по поверхности зоны.
При этом любой построенный между этими точками путь можно разбить на конечное количество отрезков ненулевой длины, проходящих либо только вне зоны неоднородности, либо внутри. Этот путь можно охарактеризовать как множество вершин ломаной P = (v1, v2, …, vn).
Решение задачи будет иметь следующий вид:
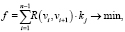
где R(vi, vi+1) – расстояние между двумя смежными точками пути, kj – весовой коэффициент отрезка пути, проходящего по поверхности зоны неоднородности.
По ходу решения задачи будут использоваться как классические алгоритмы поиска пути, так и генетические алгоритмы.
Использование классических алгоритмов поиска пути в решаемой задаче
В настоящее время для алгоритмов поиска пути актуальны два показателя – производительность алгоритма и оптимальность полученного маршрута. При этом рассматриваются различные типы задачи поиска пути и дополнительные условия:
- минимизация стоимости пути,
- динамичность окружающей среды,
- неоднородность местности,
- неполнота информации.
В общем виде постановка задачи сводится к нахождению минимума значения весовой функции маршрута. Задача имеет несколько типов представления – как на поле, разбитом на квадратные или шестиугольные ячейки и представляемом в виде планарного графа, так и на непрерывном пространстве, где позиции объектов представлены в виде непрерывных значений.
Как правило, поиск пути включает два этапа – формирование графа (как набора возможных узлов будущего маршрута) и собственно самого поискового алгоритма.
Одним из используемых в решении механизмов классических алгоритмов поиска пути являются точки видимости – при обходе препятствий можно сфокусироваться на критических точках, в основном на расположенных возле вершин препятствий [2]. На основании этого механизма образуется начальное множество потенциальных вершин, которое позже будет использоваться в генетическом алгоритме.
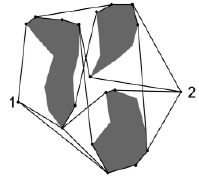
Рис. 1. Пример образования множества точек видимости
В ходе решения задачи классические алгоритмы поиска пути (в данном случае – трассировка вокруг препятствий) используются для формирования начального варианта пути, который в дальнейшем улучшается и дорабатывается. Пример образования множества точек видимости можно увидеть на рис. 1.
Адаптация генетического алгоритма к специфике решаемой задачи
Генетические алгоритмы возникли в результате наблюдения естественных процессов, происходящих в мире живых организмов, и состоят в организации эволюционного процесса, целью которого является оптимизация решения [3].
С математической точки зрения генетические алгоритмы – это алгоритмы случайного поиска, применяемые в основном для решения задач оптимизации. В них применяются аналоги механизма генетического наследования (создание следующего поколения) и естественного отбора (операции скрещивания и мутации), а также определения, заимствованные из биологии [4].
В ходе работы алгоритм формирует поколения особей по нескольким правилам, которые предполагают постепенное улучшение результата либо сохранение предыдущего уровня приспособленности [5].
Три основных типа правил:
- правила отбора – согласно этим правилам выбираются особи-родители, формирующие часть следующего поколения с помощью процесса кроссинговера,
- правила скрещивания – согласно этим правилам определяется то, каким именно будет потомок от двух определенных родителей,
- правила мутации решают, каким именно образом будет изменена конкретная особь для перехода в следующее поколение.
Классический генетический алгоритм (также называемый элементарным или простым генетическим алгоритмом) состоит из следующих этапов [6]:
1. Инициализация, или выбор исходной популяции хромосом.
2. Оценка приспособленности хромосом в популяции.
3. Проверка условия остановки алгоритма.
4. Селекция хромосом.
5. Применение генетических операторов (скрещивание, мутация).
6. Формирование новой популяции.
7. Выбор «наилучшей» хромосомы.
В рамках адаптации генетического алгоритма к задаче необходимо сопоставить понятия генетического алгоритма и задачи:
1. Особь – вариант маршрута между начальной и конечной точками, множество P = (ш1, v2, …, vn).
2. Скрещивание – процесс формирования нового маршрута из двух готовых.
3. Потомок – маршрут, являющийся результатом скрещивания или мутации.
4. Ген – отдельная вершина маршрута P, vi.
5. Популяция – набор различных маршрутов.
При адаптации применяемого генетического алгоритма используется множество потенциальных вершин, которое дополняется по ходу работы алгоритма и к которому должны принадлежать все вершины маршрутов популяции. Из этого множества могут быть взяты новые вершины для операции мутации. Начальное множество формируется при получении множества точек видимости и в дальнейшем дополняется при помощи операций мутации и образовании новых вершин при операции скрещивания.
Отдельно необходимо охарактеризовать операции скрещивания и мутации:
1. Мутация вершины – случайный выбор и малое перемещение координаты вершины, используемой в одном из маршрутов популяции, по границе зоны неоднородности. Добавление измененной вершины в множество потенциальных вершин.
2. Мутация маршрута – замена случайной вершины маршрута на одну из ближайших вершин, принадлежащих множеству потенциальных вершин.
3. Скрещивание маршрутов – представляет из себя замену случайной части одного родительского маршрута случайной частью маршрута другого родителя. При этом количество вершин в маршруте может изменяться:
Родитель 1 P1 = (v1, v2, v3, v4, v5, vm)
Родитель 2 P2 = (v1, v6, v7, v8, v9, vm)
Потомок P3 = (v1, v2, v7, v8, v4, v5, vm)
В классическом генетическом алгоритме начальная популяция формируется случайным образом, но даже при использовании вершин, полученных с помощью механизма точек видимости генерация начальной популяции займет достаточно долго время.
Для решения данной проблемы предлагается использовать классические алгоритмы поиска пути для формирования части начальной популяции. Таким образом, часть маршрутов будет создана с помощью алгоритма трассировки и другая часть случайным образом, что позволяет достаточно быстро получить начальную популяцию достаточного размера.
Блок-схема адаптированного генетического алгоритма представлена на рис. 2.
Результаты работы демонстрационной программы
Для проверки работы алгоритма была построена программа в среде Matlab. Разработка программы была разбита на два этапа – решения базовой задачи, где на рабочем поле присутствует только одна зона неоднородности, и разработка программы решения общей задачи (с присутствием множества подобных зон).
Для решения базовой задачи использовалась зона неоднородности простой формы, расположенная между начальной и конечной точками. Программа использовалась для различных вариантов весового коэффициента зоны. На рис. 3 представлено изменение оптимального маршрута при постепенном увеличении весового коэффициента.
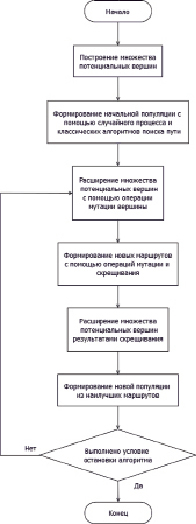
Рис. 2. Блок-схема используемого генетического алгоритма
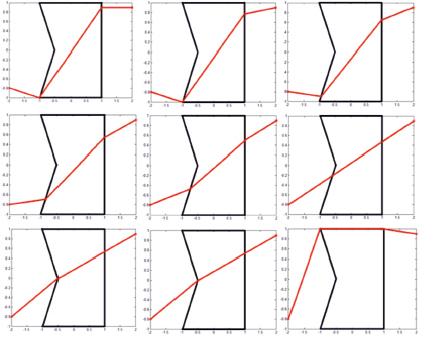
Рис. 3. Оптимальный маршрут при изменении весового коэффициента от 0 до 1,6
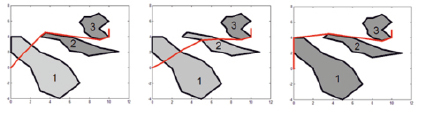
Рис. 4. Оптимальный маршрут при изменении весового коэффициента зон
Для решения общей задачи было сгенерировано рабочее поле с несколькими зонами неоднородности. По ходу решения задачи она множество раз разбивается на варианты базовой. Алгоритм был проверен при одинаковых формах и местоположении зон, но различных показателях весовых коэффициентов:
1. Коэффициенты зон неоднородности соответственно k1 = 1,5; k2 = 2; k3 = 2.
2. Коэффициенты зон неоднородности соответственно k1 = 1,5; k2 = 1,5; k3 = 2.
3. Коэффициенты зон неоднородности соответственно k1 = 2; k2 = 2; k3 = 2.
На рис. 4 представлено изменение полученного оптимального маршрута в рабочем поле при изменении весовых коэффициентов различных зон.
Заключение
В статье представлено решение, позволяющее найти оптимальный путь от начальной точки до пункта назначения на рабочем пространстве, содержащем множество зон неоднородности. При этом использовались как механизмы классических алгоритмов поиска пути, так и генетические алгоритмы. Результаты показывают работоспособность используемого алгоритма. Дальнейшим развитием работы будет оптимизация и улучшение используемого генетического алгоритма, применение его в более сложных системах.
Библиографическая ссылка
Тарасян В.С., Полушкин А.Я. ОПТИМИЗАЦИЯ ПУТИ В НЕОДНОРОДНОЙ СРЕДЕ // Фундаментальные исследования. 2017. № 10-2. С. 296-300;URL: https://fundamental-research.ru/ru/article/view?id=41828 (дата обращения: 12.01.2026).



