Мембранные системы являются основой электродиализных аппаратов, нано- и микрофлюидных устройств, работающих в разных режимах: потенциодинамическом (ПДР) и гальванодинамическом (ГДР). Теория процессов массопереноса в ПДР, когда задается скачок потенциала между двумя эквипотенциальными плоскостями, параллельными мембранам, развита в большом числе одномерных, двумерных и трехмерных математических моделей. Подробный обзор указанных моделей представлен в [1–3].
В практике электродиализа и электрохимической характеризации мембран (хронопотенциометрия, импедансометрия и др.) часто используется ГДР. Накоплено огромное количество экспериментальных данных по хронопотенциометрии [4–6], которые затруднительно интерпретировать, не имея количественной модели.
Сказанное выше привело к исследованиям в области математического моделирования ГДР. Разработки математических моделей для ГДР ведутся по нескольким направлениям.
Первое направление (метод обратной задачи) основывается на решении обратной задачи, а именно, для заданной плотности тока на межфазной границе раствор/мембрана находится соответствующий ему скачок потенциала, а далее задача превращается в ПДР [7]. При реализации этот метод требует многократного решения задачи в ПДР для одного заданного значения плотности тока, что снижает его эффективность.
Второе направление (прямой метод) основано на выводе и решении уравнения для плотности тока в диффузионном слое, вместо уравнения Пуассона для потенциала [8].
Третье направление основано на методе декомпозиции и замене системы уравнений Нернста – Планка – Пуассона системой декомпозиционных уравнений [9–11]. Последующее использование предположения о квазиравномерном распределении заряда (КРЗ или приближении закона Ома) позволяет в результате получить модель для ГДР в приближении закона Ома [12–16].
В данной статье представлен новый подход к моделированию в одномерном случае нестационарного процесса массопереноса в системах, содержащих ионообменные мембраны, в отличие от указанных выше подходов, основанного на решении уравнения Пуассона для потенциала со специально выведенным граничным условием, позволяющим задать ГДР.
Математические модели нестационарного переноса ионов бинарной соли в диффузионном слое
Моделируемая область. Рассматриваемая система представляет собой диффузионный слой раствора бинарного электролита у поверхности катионообменной мембраны (КОМ). Нормальная к поверхности мембраны координата х изменяется от 0 (внешняя граница диффузионного слоя) до δ (межфазная граница с КОМ), рис. 1.
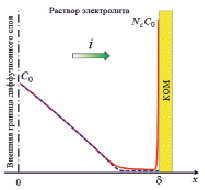
Рис. 1. Схематичные концентрационные профили катионов С1 (сплошная линия) и анионов С2 (пунктирная линия) в диффузионном слое у поверхности КОМ. Показаны плотность тока i, концентрация катионов в объеме С0 и на границе с КОМ NcС0
Система уравнений. В одномерном случае математическая модель нестационарного массопереноса состоит из системы уравнений, которая для бинарного электролита записывается следующим образом:
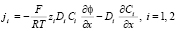 , (1)
, (1)
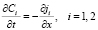 , (2)
, (2)
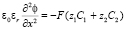 , (3)
, (3)
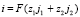 , (4)
, (4)
где ji, Di, zi – поток, коэффициент диффузии, зарядовое число и Ci молярная концентрация i-го иона, соответственно; φ – электрический потенциал; t – время; ε0 – электрическая постоянная; εr – относительная диэлектрическая проницаемость раствора электролита (предполагается постоянной); i – плотность тока; F – постоянная Фарадея; R – газовая постоянная; T – абсолютная температура. Здесь j1, j2, i, φ, C1, C2 – неизвестные функции t, x.
Уравнения Нернста – Планка (1) описывают поток ионов, обусловленный миграцией в электрическом поле и диффузией; (2) – уравнение материального баланса (в отсутствие химических реакций); (3) – уравнение Пуассона для потенциала электрического поля; (4) – плотность тока в растворе электролита.
Эта система уравнений удобна для моделирования ПДР, так как содержит дифференциальное уравнение (3) для определения потенциала.
Краевые условия для моделирования потенциодинамического режима (ПДР). Для удобства проведения сопоставительного анализа моделирования ПДР и ГДР рассмотрим сначала краевые условия для ПДР.
На внешней границе диффузионного слоя (x = 0) естественно предполагать, что выполняется условие локальной электронейтральности 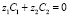 и задана концентрация электролита C0, отсюда получаем, что известна концентрация катионов и анионов:
и задана концентрация электролита C0, отсюда получаем, что известна концентрация катионов и анионов:
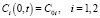 . (5)
. (5)
Так как система (1)–(4) включает потенциал электрического поля только в форме производных по пространственной координате, то существенным является только падение потенциала 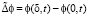 , поэтому для удобства положим
, поэтому для удобства положим
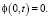 (6)
(6)
ПДР означает, что величина падения потенциала в рассматриваемой области задается известной функцией времени:
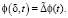 (7)
(7)
В случае потенциостатического режима 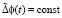 .
.
На межфазной границе раствор/КОМ (x = δ) концентрация противоионов зависит от обменной емкости КОМ, что можно задать в виде
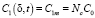 , (8)
, (8)
где постоянная Nc показывает, во сколько раз эта концентрация отличается от концентрации в объеме раствора [17].
Концентрация коионов определяется из условия непрерывности их потока у границы мембрана/раствор с учетом селективных свойств КОМ:
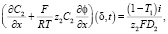 (9)
(9)
где T1 – эффективное число переноса противоионов в мембране. T1 – это число близкое к 1, причем для идеально селективной катионообменной мембраны T1 = 1 и условие (9) превращается в условие непроницаемости КОМ для коионов.
Краевая задача, включающая уравнения (1)–(4) и краевые условия (5)–(9) моделирует ПДР, причем ключевым краевым условием, определяющим его, является условие (7).
Краевые условия для моделирования ГДР. При моделировании ГДР необходимо заменить условие (7) другим условием, связанным с заданным значением плотности тока на межфазной границе раствор/мембрана 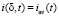 , например линейной функцией времени, константой в случае гальваностатического режима, периодической функцией времени в случае пульсирующих токов и т.д.
, например линейной функцией времени, константой в случае гальваностатического режима, периодической функцией времени в случае пульсирующих токов и т.д.
В качестве такого граничного условия на межфазной границе раствор/КОМ (x = δ) предлагается использовать соотношение, связывающее производную потенциала электрического поля на границе с заданным значением плотности тока на границе.
Для вывода такого соотношения умножим каждое из уравнений (1) на соответствующее zi и сложим, тогда с учетом формулы (4) получим
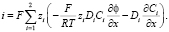 (10)
(10)
Из этого соотношения, определяя производную потенциала электрического поля 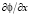 , можно получить выражение справедливое для любых точек (t, x):
, можно получить выражение справедливое для любых точек (t, x):
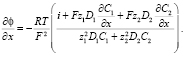 (11)
(11)
Полагая в соотношении (11), x = δ и учитывая 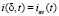 , где плотность тока iav(t) на межфазной границе является задаваемой функцией времени, получаем следующее граничное условие, определяющее производную электрического потенциала на межфазной границе через заданную на этой же границе плотность тока:
, где плотность тока iav(t) на межфазной границе является задаваемой функцией времени, получаем следующее граничное условие, определяющее производную электрического потенциала на межфазной границе через заданную на этой же границе плотность тока:
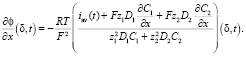 (12)
(12)
При моделировании ГДР граничное условие (12) заменяет граничное условие (7).
Остальные краевые условия для ГДР совпадают с краевыми условиями для ПДР.
Скачок потенциала в ГДР является вычисляемой величиной.
Начальные условия. Начальные условия (t = 0) зависят от целей конкретного исследования (например, моделирование развития расширенной области пространственного заряда (ОПЗ), расчет хронопотенциограмм, исследование пульсирующих токов). Так, при моделировании возникновения и развития расширенной ОПЗ в качестве начальных условий нужно выбрать стационарный массоперенос при отсутствии электрического тока (iav = 0), т.е. равновесный массоперенос.
Математическая модель ГДР в безразмерном виде
Для численного исследования краевых задач удобно перейти к безразмерному виду, так как это позволяет упростить уравнения и определить фактическое количество и набор параметров, определяющих поведение системы. Безразмерные переменные описывают класс подобных процессов, характеризующихся одинаковым значением безразмерных чисел. Для перехода к безразмерному виду используем характерные величины, описывающие задачу.
Характерные величины. При моделировании процессов массопереноса в диффузионном слое характерным значением для пространственной координаты является толщина диффузионного слоя δ, для концентраций ионов – объемная концентрация электролита C0, для коэффициентов диффузии – коэффициент диффузии электролита 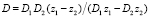 , для электрического потенциала – тепловой потенциал
, для электрического потенциала – тепловой потенциал 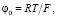 для потока ионов – диффузионный поток
для потока ионов – диффузионный поток 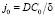 , для плотности тока – величина
, для плотности тока – величина 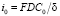 , которая представляет собой половину предельной плотности тока
, которая представляет собой половину предельной плотности тока 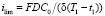 [1], при числах переноса катионов в мембране T1 = 1 и в растворе t1 = 0,5. Тогда, в качестве характерного времени получаем
[1], при числах переноса катионов в мембране T1 = 1 и в растворе t1 = 0,5. Тогда, в качестве характерного времени получаем 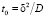 , имеющий смысл диффузионного времени, т.е. времени, необходимого для выравнивания концентрации диффундирующего вещества.
, имеющий смысл диффузионного времени, т.е. времени, необходимого для выравнивания концентрации диффундирующего вещества.
Формулы перехода. Переведем уравнения в безразмерную форму с помощью соотношений (индексом (u) обозначены безразмерные варианты величин):
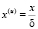 ,
, 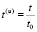 ,
,
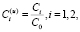
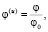
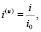
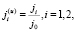
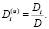 (13)
(13)
Система уравнений в безразмерной форме (индекс (u) для простоты записи опущен):
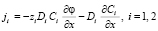 , (14)
, (14)
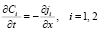 , (15)
, (15)
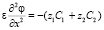 , (16)
, (16)
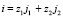 . (17)
. (17)
Система уравнений (14)–(17) содержит одно безразмерное число 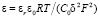 . Физический смысл малого параметра ε состоит в том, что это есть удвоенный квадрат отношения дебаевской длины lD к толщине диффузионного слоя δ:
. Физический смысл малого параметра ε состоит в том, что это есть удвоенный квадрат отношения дебаевской длины lD к толщине диффузионного слоя δ: 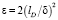 [1]. Оценка величины ε показывает, что при естественных для электродиализа условиях оно имеет порядок 10–10 – 10–4.
[1]. Оценка величины ε показывает, что при естественных для электродиализа условиях оно имеет порядок 10–10 – 10–4.
Для удобства численного решения преобразуем систему уравнений, подставив плотность потока (14) в уравнения (15) и (17):
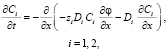 (18)
(18)
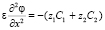 , (19)
, (19)
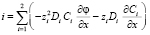 . (20)
. (20)
Таким образом, система уравнений содержит четыре неизвестные функции t, x: C1, C2, φ, i. Поля концентраций C1, C2 и потенциала φ определяются решением уравнений (18) и (19) соответственно. Плотность тока i вычисляется с помощью выражения (20). Присутствие малого параметра ε в уравнении Пуассона (19) обуславливает сингулярное возмущение краевой задачи, что значительно усложняет ее численное решение. Потенциал электрического поля φ и концентрации ионов c1, c2 изменяются очень быстро в узком пограничном слое, толщина которого близка к длине Дебая lD [1]. Одним из возможных подходов решения этой проблемы является уплотнение вычислительной сетки в пограничном слое.
Краевые условия ГДР в безразмерной форме. На внешней границе диффузионного слоя x = 0:
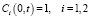 ,
, 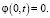 (21)
(21)
На границе раствор/КОМ x = 1:
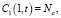
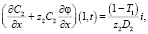
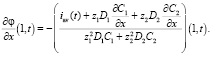 (22)
(22)
Численное решение найдено методом конечных элементов с помощью пакета Comsol Multiphysics [18].
Возникновение и развитие расширенной ОПЗ в ГДР
Рассмотрим процесс возникновения и развития расширенной ОПЗ для ГДР, увеличивая плотность тока от 0 до запредельных значений по формуле: iav(t) = at, где a = 0,0041ilim. На рис. 2 приведен график безразмерной плотности пространственного заряда 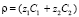 в координатах t и x.
в координатах t и x.
Из рис. 2 видно, что область пространственного заряда начинает формироваться в момент времени t = 245, когда плотность тока равна предельной iav(t) = ilim. С увеличением плотности тока толщина расширенной ОПЗ увеличивается.
Сопоставительный анализ моделей ПДР и ГДР
Сопоставим результаты численного исследования с помощью моделей для ГДР при iav(t) = const и для ПДР при Δφ(t) = const. Выполнены расчеты по предлагаемой ГДР модели (рис. 3), при ε = 3•10–7 для следующих значений плотности тока iav = 0,9ilim, ilim = 1,1ilim. Здесь 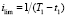 – безразмерная предельная плотность тока, определенная по формуле Пирса [1] (T1 = 0,972, t1 = 0,395).
– безразмерная предельная плотность тока, определенная по формуле Пирса [1] (T1 = 0,972, t1 = 0,395).
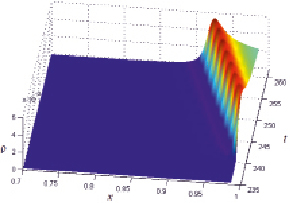
Рис. 2. Плотность пространственного заряда ρ в расширенной ОПЗ (отброшены области квазиравновесного пространственного заряда справа и электронейтральности слева). Результаты расчетов по ГДР модели при ε= 3•10–7 для плотности тока iav(t) = at, a = 0,0041ilim
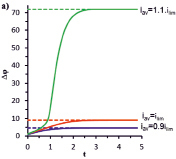
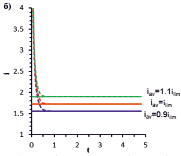
Рис. 3. a – зависимость скачка потенциала от времени; б – зависимость средней плотности тока от времени. Результаты расчетов по ГДР модели (сплошные линии) и ПДР модели (пунктирные линии) при ε = 3•10–7 для плотности тока iav = 0,9ilim, ilim = 1,1ilim
Из рис. 3, а видно, что с течением времени скачок потенциала увеличивается и достигает стационарного значения Δφst (причем с увеличением iav увеличивается и Δφst). Для значений скачка потенциала Δφst, соответствующих стационарному состоянию при iav = 0,9ilim, ilim = 1,1ilim, выполнен расчет по модели для ПДР (пунктирные линии на рис. 3).
На рис. 4 приведены концентрационные профили в момент времени t = 5 (когда достигнуто стационарное состояние), рассчитанные по моделям для ГДР (сплошные линии) и ПДР (пунктирные линии). При плотности тока iav = 0,9ilim в области у поверхности мембраны концентрации ионов уменьшаются, диффузионный слой разделен на две области: электронейтральную (0 < x ≤ δ2) и ОПЗ (δ2 < x ≤ 1); при iav = ilim – концентрации ионов на границе с мембраной истощены почти до нулевого значения; при iav = 1,1ilim – в структуре ОПЗ можно выделить расширенную ОПЗ (δ1 < x ≤ δ2) и квазиравновесную (δ2 < x ≤ 1). Описанное поведение системы соответствует современным представлениям о структуре диффузионного слоя при различных значениях тока [3].
Из рис. 3 и 4 видно, что результаты вычислений в стационарном состоянии по моделям для ГДР и ПДР полностью согласуются.
Заключение
В статье предложен новый метод математического моделирования нестационарного процесса массопереноса в ГДР в мембранных системах в одномерном случае с использованием уравнения Пуассона и специального граничного условия, позволяющего задать ГДР. Предлагаемый метод моделирования может быть расширен для двумерных и трехмерных случаев, дополнен уравнениями Навье – Стокса и полезен в исследованиях гравитационной конвекции и электроконвекции в ГДР.
Проведен сопоставительный анализ различных методов моделирования ГДР, результаты которого приведены в таблице.
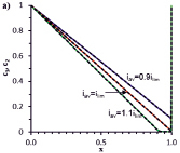
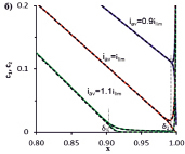
Рис. 4. а – концентрационные профили; б – увеличение рис. а. Результаты численного расчета по моделям для ГДР (сплошные линии) и ПДР (пунктирные линии) в момент t = 5 при ε = 3•10–7, плотности тока iav = 0,9ilim, ilim = 1,1ilim
Сопоставительный анализ различных методов моделирования ГДР
|
Метод Характеристика |
Метод обратной задачи |
Прямой метод |
Метод, основанный на методе декомпозиции |
Косвенный метод: уравнение Пуассона и специальное граничное условие |
|
Область применения |
Любые задачи |
Любые задачи |
Любые задачи |
Любые задачи |
|
Вычислительная трудоемкость |
Очень высокая |
Средняя |
Низкая |
Средняя |
|
Математическая сложность |
Средняя |
Высокая |
Очень высокая |
Низкая |
|
Сложность вывода упрощенных моделей |
Высокая |
Очень низкая |
Очень низкая |
Средняя |
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта: № 16-08-00128 А «Теоретическое и экспериментальное исследование гравитационной конвекции в мембранных системах с учетом реакции диссоциации/рекомбинации молекул воды».
Библиографическая ссылка
Узденова А.М., Уртенов М.Х. КОСВЕННЫЙ МЕТОД МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ ГАЛЬВАНОДИНАМИЧЕСКОГО РЕЖИМА МАССОПЕРЕНОСА В ДИФФУЗИОННОМ СЛОЕ У ИОНООБМЕННОЙ МЕМБРАНЫ // Фундаментальные исследования. 2017. № 9-1. С. 105-111;URL: https://fundamental-research.ru/ru/article/view?id=41712 (дата обращения: 17.11.2025).
DOI: https://doi.org/10.17513/fr.41712



