Главная концепция приведенного в [1] механизма появления восходящего закрученного потока воздуха в атмосфере состоит в том, что при прогреве части поверхности суши или поверхности воды возникает мощный восходящий поток воздуха. Радиальное (замещающее восходящий поток) течение воздуха, имеющее направление к центру области нагрева, за счет силы инерции Кориолиса приобретает закрутку вокруг оси в положительном направлении для Северного полушария.
Данная схема экспериментально доказана в работе [2]. Статья [2] содержит описания экспериментов, в которых свободный вихрь генерировался нагревом снизу металлической круглой пластины газовой горелкой.
Попытка математически и численно смоделировать появление и дальнейшее изменение подобного закрученного восходящего потока воздуха при нагреве поверхности Земли была предпринята в работе [3]. Численные расчеты и тщательный разбор возникающих сложных течений сжимаемого вязкого теплопроводного газа в начальной фазе формирования закрученного восходящего потока, вызванного локальным нагревом подстилающей поверхности, показали перемещение газа в двух встречных направлениях. Одно направлено по радиусу от центра нагрева к его границе, а другое направлено в противоположном направлении – от периферии к области нагрева.
Так как перемещающиеся вдоль поверхности Земли частицы газа из-за действия силы инерции Кориолиса отклоняются вправо то, следовательно, противоположно направленные потоки имеют противоположные направления закрутки. С этим связано возникновение нескольких локальных вихрей с противоположной направленностью вращения [3]. Это и подтверждается выполненными расчетами.
Кроме тропических циклонов и торнадо в природе встречаются [4] и так называемые огненные вихри, имеющие другое направление закрутки: отрицательное в Северном полушарии и положительное в Южном полушарии. Строго математически [5] получено решение системы уравнений газовой динамики, которое описывает появление отрицательной закрутки в радиальном течении идеального газа вокруг нагревающейся поверхности вертикального цилиндра.
Экспериментально [6] без дополнительной закрутки были созданы течения, похожие на наблюдаемые в природе огненные вихри. В работе [6] продемонстрирована принципиальная возможность физического моделирования свободных концентрированных огненных вихрей в лабораторных условиях без использования закручивающих устройств от нескольких источников нагрева. Подробно описана экспериментальная установка для генерирования свободных огненных вихрей и проведен детальный анализ особенностей их возникновения. Покадровая фиксация позволяет получать данные об основных параметрах процесса генерации огненных вихрей и их интегральных характеристиках.
Целью данной работы является численное моделирование и детальный анализ скоростных характеристик сложных течений сжимаемого вязкого теплопроводного политропного газа на начальном этапе появления закрученного восходящего потока, инициированного нагреванием подстилающей поверхности пятью источниками.
Математическая модель и ее численная реализация
Для описания сложных трехмерных и нестационарных течений сжимаемого политропного газа, обладающего диссипативными свойствами, в работе используется полная система дифференциальных уравнений Навье – Стокса. Записанная в безразмерных переменных с учетом гравитации и вращения Земли в векторной форме она может быть записана так [7]:
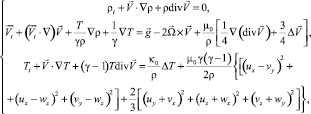 (*)
(*)
где значения безразмерных коэффициентов вязкости и теплопроводности равны соответственно μ0 = 0,001, κ0 ≈ 1,46μ0. Эта система является дифференциальной формой законов сохранения массы, импульса и энергии в движущейся сплошной среде.
В системе (1) также: x, y, z – декартовы координаты; t - время; ρ – плотность; T - температура газа; 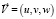 – вектор скорости частиц газа с проекциями на соответствующие декартовы оси координат; γ = 1,4 – показатель политропы для воздуха;
– вектор скорости частиц газа с проекциями на соответствующие декартовы оси координат; γ = 1,4 – показатель политропы для воздуха; 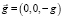 – вектор ускорения силы тяжести;
– вектор ускорения силы тяжести; 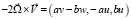 – вектор ускорения Кориолиса, где параметры
– вектор ускорения Кориолиса, где параметры 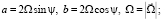
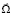 – вектор угловой скорости вращения Земли; ψ – широта точки O – начала декартовой системы координат xyzO, вращающейся вместе с Землей;
– вектор угловой скорости вращения Земли; ψ – широта точки O – начала декартовой системы координат xyzO, вращающейся вместе с Землей; 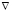 и div – операторы градиента и дивергенции по декартовым переменным, а точкой обозначено скалярное произведение векторов.
и div – операторы градиента и дивергенции по декартовым переменным, а точкой обозначено скалярное произведение векторов.
За начальные условия принимается следующий набор функций, задающих точное решение системы (*) [8]:
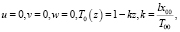
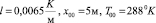 ,
,
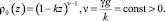
Расчетной областью является куб с длинами сторон 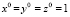 .
.
На нижней грани z = 0 расчетной области вертикальная составляющая скорости газа полагалась равной нулю, то есть w = 0. Постепенный же нагрев до температуры 300 °C в пяти областях моделировался следующей функциональной зависимостью температуры от координат точек и времени нагрева
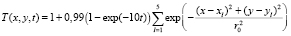 .
.
Здесь r0 = 0,025 – безразмерное значение эффективных радиусов областей нагрева; 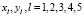 – координаты пяти центров нагрева нижней грани расчетной области, расположенных на диагоналях квадрата и в точке их пересечения. Две другие составляющие скорости газа и плотность на нижней грани расчетной области брались из условия непрерывности потока газа [9]. На остальных пяти гранях расчетной области для всех пяти газодинамических характеристик – плотности, температуры и трех компонент вектора – скорости брались из условия непрерывности [9].
– координаты пяти центров нагрева нижней грани расчетной области, расположенных на диагоналях квадрата и в точке их пересечения. Две другие составляющие скорости газа и плотность на нижней грани расчетной области брались из условия непрерывности потока газа [9]. На остальных пяти гранях расчетной области для всех пяти газодинамических характеристик – плотности, температуры и трех компонент вектора – скорости брались из условия непрерывности [9].
Другими словами, выбранные граничные условия моделируют процесс возникновения трехмерных и нестационарных течений вязкого сжимаемого политропного теплопроводного газа при локальном нагреве пятью источниками нижней грани с возможностью свободного движения газа через все грани, кроме нижней грани.
В расчетной области строится прямоугольная сетка узлов следующим образом: 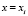 ,
, 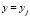 ,
, 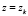 . Здесь
. Здесь 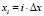 ,
, 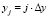 ,
, 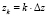 ,
, 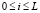 ,
, 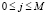 ,
, 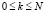 . Соответственно выбираются разностные шаги по пространственным переменным
. Соответственно выбираются разностные шаги по пространственным переменным 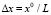 ,
, 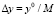 ,
, 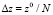 .
.
Расчетные шаги по пространственным переменным 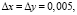
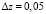 , а расчетный шаг по времени
, а расчетный шаг по времени 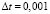 . При таком выборе расчетных шагов по пространству и времени обеспечивается устойчивость вычислительного процесса, то есть выполняются условия Куранта:
. При таком выборе расчетных шагов по пространству и времени обеспечивается устойчивость вычислительного процесса, то есть выполняются условия Куранта:
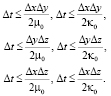
Численно решая полную систему уравнений Навь – Стокса, с указанными выше начальными и краевыми условиями, по явной разностной схеме находятся значения искомых функций в каждом из узлов на любом расчетном по времени шаге [3].
Результаты расчетов
На рис. 1–3 представлены результаты расчета трех компонентов скоростей возникающего при нагреве нижней грани расчетной области потока воздуха для среднего значения высоты 0,5 м в конкретные фиксированные моменты времени. По осям Ox и Oy откладываются номера узлов расчетной сетки.
На рис. 1–2 приведены графики x-ой и y-ой компонент скоростей течений газа в момент времени t = 0,5 мин.
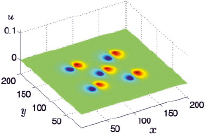
Рис. 1. x-ая компонента скорости
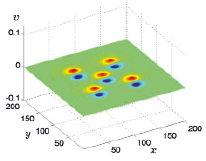
Рис. 2. y-ая компонента скорости
Основными видами течений воздуха в указанный момент времени являются расходящиеся потоки воздуха от областей локального нагрева, которые с течением времени приобретают отрицательную закрутку (по часовой стрелке, если смотреть на поток сверху).
На рис. 3 представлен график рассчитанной z-ой компоненты скорости в тот же момент времени.
Из рисунка видно, что в указанный момент времени фиксируется возникновение вертикально направленных потоков воздуха над источниками нагрева. Максимальные значения вертикальных скоростей соответствуют точкам расположения источников нагрева и постепенно уменьшаются до нулевых значений при удалении от них.
На рис. 4–5 приведены результаты рассчитанных мгновенных линий тока для моментов времени t1 = 1 минута и t2 = 3 минуты. По осям Ox и Oy откладываются безразмерные значения расстояния.
Представленные на рисунках линии тока показывают, что возникающие при локальном нагреве несколькими источниками потоки воздуха имеют нестационарный сложный характер. Основной особенностью этих течений является закрутка, имеющая противоположные направления (как положительные, так и отрицательные). В результате происходит интенсивное перемешивание потоков воздуха не только в горизонтальных плоскостях, но и в вертикальных плоскостях.
Из результатов расчетов компонентов скоростей можно выделить следующие последовательные фазы возникновения тепловых вихрей. Первая фаза характеризуется возникновением пяти локальных, расходящихся от областей нагрева потоков газа. Эти потоки газа приобретают отрицательную закрутку. Вторая фаза связана с появлением локальных вихрей с противоположной направленностью вращения. С наступлением третьей фазы, как следует из расчетов, возникает общее встречное движение потоков газа от периферии к центру. Это встречное радиальное движение под действием силы Кориолиса приобретает положительную закрутку. Указанные этапы формирования теплового потока не имеют четко выраженных временных границ, плавно сменяя друг друга, или даже могут происходить одновременно. Тем не менее характерные черты каждого из этих этапов позволяют расположить их в хронологической последовательности.
Кроме того, расчеты показали, что с течением времени преобладающим становится течение с положительным направлением закрутки.
Заключение
Проведено численное моделирование и подробное исследование скоростных характеристик течений сжимаемого вязкого политропного теплопроводного газа на начальном этапе зарождения закрученного восходящего потока, который инициируется пятью источниками нагрева.
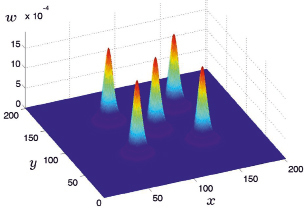
Рис. 3. z-ая компонента скорости
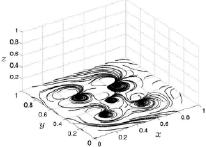
Рис. 4. Линии тока при t1 = 1 мин

Рис. 5. Линии тока при t2 = 3 мин
За основную математическую модель для представления сложных трехмерных нестационарных течений сжимаемого политропного газа, обладающего диссипативными свойствами вязкости и теплопроводности, принимается полная система уравнений Навье – Стокса. Начальными условиями являлись пять функций, которые задают точное решение полной системы дифференциальных уравнений Навье – Стокса.
На нижней грани расчетной области вертикальная составляющая скорости газа полагалась равной нулю. Постепенный нагрев в пяти областях моделировался функциональной зависимостью температуры от координат точек и времени нагрева.
Проведен расчет трех компонентов скоростей возникающего при нагреве нижней грани расчетной области потока воздуха, а также построены мгновенные линии тока. Показано, что возникающие при локальном нагреве несколькими источниками потоки воздуха имеют нестационарный сложный характер с противоположными направлениями вращения с постепенным преобладанием положительной закрутки.
Библиографическая ссылка
Баранникова Д.Д., Обухов А.Г. РАСЧЕТ СКОРОСТНЫХ ХАРАКТЕРИСТИК ВОСХОДЯЩЕГО ЗАКРУЧЕННОГО ПОТОКА С ПЯТЬЮ ИСТОЧНИКАМИ НАГРЕВА // Фундаментальные исследования. 2017. № 9-1. С. 14-18;URL: https://fundamental-research.ru/ru/article/view?id=41696 (дата обращения: 16.01.2026).



