В настоящее время приобрело особую значимость развитие робототехники [1]. В связи с этим важным является решение задач, связанных с искусственным интеллектом [2]. Однако создаваемые математические модели и алгоритмы «психологического» поведения роботов рассматривают роботов с абсолютной памятью [3], т.е. роботов, не способных забывать прошлое. Также мало уделяется внимания поведению групп эмоциональных роботов, способных забывать информацию [1] и являющихся наиболее близкими по своей «психологии» к человеку по сравнению с роботами с абсолютной памятью. Настоящая статья посвящена математическому моделированию поведения таких групп.
Математическая модель воспитания отдельного робота
В работах [4, 5] приведено соотношение, позволяющее вычислять воспитание робота, получаемое им в результате непрерывного воздействия на него сюжетами и порождающимися в результате этого у него воспитаниями:
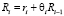 , (1)
, (1)
где i – порядковый номер сюжета (такта), воздействующего на робота и порождающего у него элементарное воспитание ri, Ri – суммарное воспитание робота, полученное им в результате воздействия на него общего количества сюжетов, равных величине i, R0 = 0, θi – коэффициент памяти, характеризующий долю предыдущего суммарного воспитания, которую помнит робот к моменту воздействия на него сюжетом с порядковым номером i, 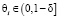 ,
, 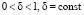 .
.
Предположим, что ri = q = const, q > 0, θi = θ, R0 = 0. Легко видеть, что в рамках этих допущений соотношение (1) представляет собой сумму членов геометрической прогрессии, которая описывается известной формулой [6]:
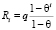 . (2)
. (2)
Докажем следующую теорему.
Теорема 1.
Для забывчивого робота с равноценными положительными ограниченными эмоциями воспитание ограничено.
Доказательство.
Так как робот забывчив, то по определению таких роботов существует число C, удовлетворяющее неравенству 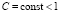 , причем справедлива формула
, причем справедлива формула
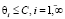 .
.
Так как робот обладает равноценными эмоциями, то справедливо равенство
ri = q = const > 0, 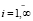 .
.
Очевидна следующая цепочка соотношений:
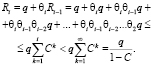 (3)
(3)
Таким образом, воспитание робота Ri ограничено.
Что и требовалось доказать.
На основе теоремы 1 сформулируем и докажем следующее утверждение.
Теорема 2.
Если элементарное воспитание ri забывчивого робота удовлетворяет неравенств
0 < ri ≤ q = const > 0, 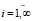 ,
,
то воспитание робота ограничено.
Доказательство.
Воспитание робота Bi удовлетворяет соотношению
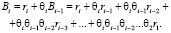
Вычтем из величины Ri задаваемую формулой (3) величину Bi, тогда получим
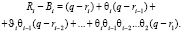 (4)
(4)
В силу условий теоремы 2 справедливы неравенства 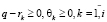 , из которых следует согласно формуле (4) соотношение
, из которых следует согласно формуле (4) соотношение
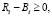 то есть
то есть 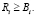
Так как справедливы формулы 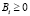 и
и 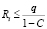 , то воспитание Bi ограничено.
, то воспитание Bi ограничено.
Что и требовалось доказать.
Математическая модель воспитания группы роботов
В настоящее время практически не изучен вопрос о построении математических моделей воспитания группы роботов. Один из подходов для изучения этой темы предложен в работе [7]. Основываясь на этом подходе, предложим простейшие модели воспитания группы роботов при непрерывном и одновременном воспитании каждого робота – члена этой группы.
Пусть n – количество роботов в группе, j – порядковый номер робота в этой группе, 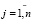 ,
, 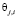 – коэффициент памяти робота к моменту воздействия на него сюжетом с порядковым номером i,
– коэффициент памяти робота к моменту воздействия на него сюжетом с порядковым номером i, 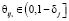 ,
, 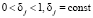 , rj,i – элементарное воспитание робота j, Rj,i – суммарное воспитание робота, полученное им в результате воздействия на него общего количества сюжетов.
, rj,i – элементарное воспитание робота j, Rj,i – суммарное воспитание робота, полученное им в результате воздействия на него общего количества сюжетов.
При введенных обозначениях аналогично соотношению (1) введем следующее равенство
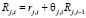 . (5)
. (5)
По аналогии с формулой (5) будем считать, что суммарное воспитание группы роботов определяется формулой
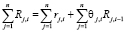 . (6)
. (6)
Разделив обе части равенства (6) на величину n, получим соотношение
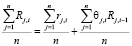 . (7)
. (7)
Введем следующие обозначения
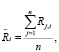
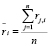 .
.
Согласно введенным обозначениям равенство (7) примет вид
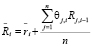 . (8)
. (8)
Математическая модель групповой памяти роботов
Пусть
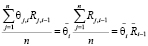 . (9)
. (9)
С учетом (9) формула (8) примет вид
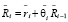 . (10)
. (10)
Аналогично терминам моделирования воспитания отдельного робота величину 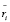 назовем элементарным воспитанием группы роботов, а значение
назовем элементарным воспитанием группы роботов, а значение 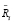 – воспитанием этой группы в конце такта с порядковым номером i.
– воспитанием этой группы в конце такта с порядковым номером i.
Нетрудно заметить, что согласно соотношению (9) справедливо равенство
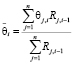 . (11)
. (11)
Коэффициент 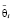 назовем коэффициентом групповой памяти роботов. Нетрудно заметить, что в общем случае коэффициент групповой памяти для каждого такта может быть собственным.
назовем коэффициентом групповой памяти роботов. Нетрудно заметить, что в общем случае коэффициент групповой памяти для каждого такта может быть собственным.
Очевидно, что коэффициент групповой памяти роботов при rj,i > 0 удовлетворяет соотношению 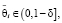
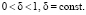
Легко видеть, что если справедливы равенства 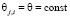 ,
, 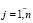 , то согласно формуле (11) верно соотношение
, то согласно формуле (11) верно соотношение 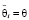 , т.е. группа роботов является равномерно забывчивой [5, 6] вне зависимости от численных значений элементарных воспитаний каждого робота группы.
, т.е. группа роботов является равномерно забывчивой [5, 6] вне зависимости от численных значений элементарных воспитаний каждого робота группы.
Исследуем математические свойства коэффициента групповой памяти для некоторых частных случаев.
Случай 1. Пусть каждый робот в группе имеет равноценные эмоции и каждый робот является равномерно забывчивым [5], т.е., справедливы равенства 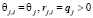 .
.
Легко видеть, что при этих условиях соотношение (11) примет вид
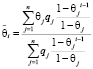 . (12)
. (12)
Случай 2. Пусть 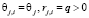 .
.
Нетрудно заметить, что в этом случае равенство (12) примет вид
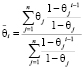 . (13)
. (13)
Равенство (13) позволяет сделать вывод о том, что равноценность эмоций всех роботов в группе и равномерная забывчивость [5] каждого робота по отдельности не влечет равномерную забывчивость всей группы роботов в целом.
Случай 3. Пусть выполняется условие 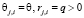 .
.
Преобразование формулы (12) позволяет получить равенство 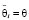 , на основе которого можно сформулировать вывод о том, что равноценность эмоций каждого из роботов в группе и одинаковая равномерная забывчивость всех роботов группы влечет равномерную забывчивость всей группы роботов. Нетрудно заметить, что в этом случае воспитание группы роботов описывается воспитанием любого отдельного робота из этой группы.
, на основе которого можно сформулировать вывод о том, что равноценность эмоций каждого из роботов в группе и одинаковая равномерная забывчивость всех роботов группы влечет равномерную забывчивость всей группы роботов. Нетрудно заметить, что в этом случае воспитание группы роботов описывается воспитанием любого отдельного робота из этой группы.
Согласно формуле (12) очевидна цепочка равенств
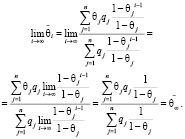 (14)
(14)
Соотношения (14) позволяют сформулировать следующий вывод:
– Коэффициент групповой памяти равномерно забывчивых роботов с равноценными эмоциями при непрерывном воспитании имеет предел.
Рассмотрим следующий пример. Пусть n = 2, q1 = 1, q1 = 2, θ1 = 0,5, θ1 = 0,8.
Вычисления показывают, что для этого примера предельное значение коэффициента групповой памяти θ∞ удовлетворяет равенству θ∞ = 0,75.
Изменение значений коэффициента групповой памяти  роботов, вычисленного по формуле (12), проиллюстрировано графиком на рисунке.
роботов, вычисленного по формуле (12), проиллюстрировано графиком на рисунке.
Анализ графика позволяет утверждать, что группа равномерно забывчивых роботов может не быть равномерно забывчивой в целом.
Основываясь на соотношении (10), можно сформулировать теорему 3 для группы роботов, аналогичную теореме 2, которая доказана для отдельного робота.
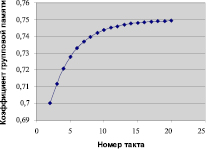
График изменений коэффициента групповой памяти роботов
Теорема 3.
Если элементарное воспитание 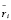 группы забывчивых роботов удовлетворяет неравенству
группы забывчивых роботов удовлетворяет неравенству
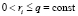 ,
, 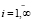 ,
,
то воспитание группы роботов ограничено.
Так как логика доказательства теоремы 3 копирует доказательство теоремы 2, то мы не будем ввиду очевидности повторять это доказательство.
Пусть каждый робот в группе обладает абсолютной памятью, тогда справедлива цепочка равенств
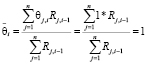 . (15)
. (15)
Соотношение (15) позволяет сделать вывод о том, что абсолютная память каждого робота из группы влечет абсолютную память всей группы в целом.
Модель забывания воспитания группой роботов
Пусть стимулы, порождающие элементарные воспитания у группы роботов, отсутствуют. Обозначим количество пропусков стимулов символом k. Аналогично определению фиктивных тактов отдельного робота [5, 6] каждый пропуск стимулов при воспитательном процессе группы роботов назовем фиктивным тактом группы.
Тогда из равенства (10) следует, что группа роботов будет забывать воспитание согласно соотношению
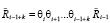 .
.
Очевидно, что для равномерно забывчивой группы забывание группового воспитания удовлетворяет формуле
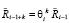 . (16)
. (16)
Соотношение (16) позволяет сделать вывод о том, что группа равномерно забывчивых роботов забывает воспитание согласно закону показательной функции от параметра количества k фиктивных тактов группы.
Заключение
Приведенные математические модели могут быть использованы при проектировании роботов, составляющих группу с заданными свойствами, касающимися особенностей памяти этой группы, на основе индивидуальных памяти и воспитания каждого робота из группы.
Доказанные теоремы и результаты исследований математических моделей, описанные в статье, позволяют прогнозировать воспитание группы роботов и забывание воспитания группой в зависимости от воспитательного процесса, включающего фиктивные такты, каждого члена группы.
Библиографическая ссылка
Пенский О.Г., Ощепкова Н.В. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ГРУППОВОЙ ПАМЯТИ РОБОТОВ // Фундаментальные исследования. 2017. № 8-2. С. 298-301;URL: https://fundamental-research.ru/ru/article/view?id=41664 (дата обращения: 19.12.2025).



