Работа посвящена математическому моделированию в страховании. На основе применения методов моделирования реальных статистических данных построена и реализована модель в среде моделирования AnyLogic. Имитационное моделирование – одно из направлений математического моделирования, являющееся мощным инструментом анализа сложных систем и явлений. В процессе создания модели проводится анализ изучаемого объекта и его поведения. Далее собранные статистические данные представляются в виде, пригодном для реализации и исследования с помощью операций в специализированном программном обеспечении на компьютере. Имитационная модель позволяет воспроизвести протекающие в изучаемом объекте или с его участием процессы так, как они происходили бы в действительности [1]. При изучении многочисленных литературных источников по имитационному моделированию [2, 3] были рассмотрены разнообразные методы и подходы к построению имитационных моделей.
Обработка статистических данных
В качестве непосредственного объекта анализа выбрана страховая компания N, в которой тенденции развития страховых выплат из года в год выражены в явном виде. Для проведения расчетов произведен сбор информации о значениях всех денежных выплат по договорам ОСАГО за три года. Данные о количестве ДТП за указанный период представлены на рис. 1.
Отмечено, что повышение сумм выплат по ОСАГО в связи с увеличением количества ДТП происходит с ноября по март. Это можно объяснить неблагоприятными погодными условиями, создающими трудности управления и маневрирования на сезонном дорожном покрытии для автомобилистов. На основании обработанных эмпирических данных сделаны выводы о сезонном характере зависимости сумм выплат и количества страховых случаев от месяца года. Максимальные суммы выплат и число ДТП отмечаются в декабре.
При помощи статистических методов произведен анализ объема денежных выплат в случаях ДТП по страховым полисам ОСАГО за 3 года, построен интервальный вариационный ряд распределения по величине страховых выплат для каждого года. Обработка материала позволила получить исходные данные для расчета и анализа, что позволило построить имитационную модель выплат.
Идентификация характера распределения данных
При оценке характера распределения данных были найдены показатели центра распределения, показатели вариации, средняя ошибка выборки для каждого месяца и по годам. Для проверки гипотезы о виде распределения сумм выплат применялся критерий согласия Пирсона. В результате анализа характера статистических данных была получена информация о законе распределения денежных выплат в случаях ДТП. После исследования данных по годам авторами был сделан вывод о том, что 7 месяцев в году распределены по нормальному закону, а 5 – имеют распределение Пуассона.
Проведенные расчеты позволяют сделать качественные и количественные выводы о характеристиках изучаемого процесса. По результатам исследований на основе полученных данных реализована имитационная модель системы денежных выплат по полисам ОСАГО для прогнозирования возможных расходов страховой компании в данной сфере деятельности [4, 5].
Имитационная модель денежных выплат в случаях ДТП
Из анализа полученных статистических данных и характера распределений денежных выплат следует, что не все выплаты распределены по нормальному закону, поэтому реализацию модели системы прогнозирования страховых сумм решено рассматривать на основе двух месяцев - января и февраля, имеющих разные виды распределения.
Для имитации объемов выплат, подчиняющихся нормальному распределению, применим центральную предельную теорему: сумма n одинаково распределенных случайных величин стремится к нормально распределенной величине при бесконечном увеличении n [6]. Данный результат можно использовать для получения значений, соответствующих нормальному распределению с математическим ожиданием μ и стандартным отклонением σ. Случайная величина, подчиняющаяся нормальному распределению N(μ, σ), может быть получена из случайной величины x по формуле
y = μ + σx.
Для нахождения случайной величины x применим процедуру решения, в соответствии с которой используется преобразование
,
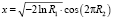где R1, R2 – случайные величины, равномерно распределенные в промежутке [0, 1].
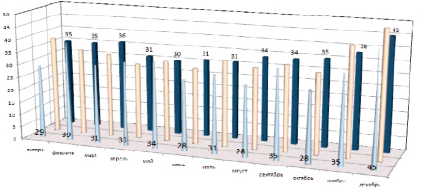
Рис. 1. Численность ДТП за три года
Бокс и Мюллер доказали, что случайная величина x является стандартной нормально распределенной случайной величиной, т.е. имеет распределение N(0, 1) [1]. Следовательно, y = μ + σx дает значение, подчиняющееся нормальному распределению N(μ, σ). Эта процедура является более эффективной, так как требует генерирования всего двух случайных чисел из отрезка [0, 1].
На основании обработки и анализа исходных данных, полученных за январь, можем отметить, что вероятность отсутствия выплат в какой-либо день равна 16 %. Следовательно, для определения дней, в которых не будет ДТП, зададим ряд случайных чисел на промежутке [0, 1]. Величины, значения которых меньше значения 0,16, будут отображать дни без выплат по ДТП. Отметим эти дни 0, остальным дням, с выплатами, присвоим значение 1. После зададим два ряда случайных чисел, равномерно распределенных на промежутке [0, 1], и применим метод Бокса – Мюллера [7] для нахождения значений x, подчиняющихся нормальному распределению. Далее, применяя формулу y = μ + σx, вычислим значения выплат y. Значения данной модели выплат представлены ниже (pис. 2).
Рассмотрим построение имитационной модели для распределения Пуассона [8] на примере математической обработки исходных данных, полученных за февраль. Для данного распределения необходимо получить случайное значение, соответствующее распределению Пуассона с математическим ожиданием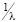 
. Для этого применим формулу
,
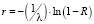где r – сгенерированное значение случайной величины выплаты, R – случайное число из интервала [0, 1].
Так как R – случайное число из [0, 1], то и (1 – R) представляет собой случайное число из того же промежутка, поэтому (1 – R) в формуле можно заменить на R. Вероятность того, что выплаты не будет, для февраля равна 10 %.
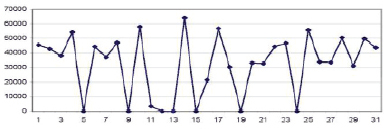
А) Реализация имитационной модели по нормальному закону
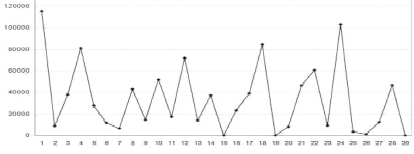
Б) Реализация имитационной модели по закону Пуассона
Рис. 2. Реализация имитационной модели
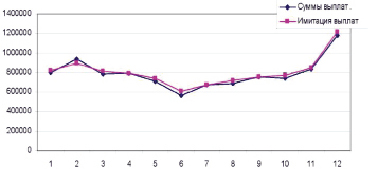
Рис. 3. Проверка адекватности построенной модели
В результате построения имитационных моделей за каждый месяц стало возможным спрогнозировать итоговую сумму выплат за год. На основе данных моделей проведены исследования изменчивости сумм выплат. Для проверки адекватности данных моделей проведена прогонка случайных величин на промежутке [0, 1]. Для каждого месяца данные сумм выплат были зафиксированы. Прогонка для каждого месяца осуществлялась 20 раз. Далее рассчитывалось среднее значение величины выплат за каждый месяц. Результаты исследования модели представлены на рисунке (рис. 3).
Построенная модель выплат отражена на графике вместе с данными исходного года. Динамика построенной модели близка к исходным данным. Колебания значений динамики разницы между значениями построенной имитационной модели не превышают 5 % исходных данных сумм выплат за год.
Анализ надежности страховой компании
Моделировать суммы выплат по страховым полисам в течение месяца будем, используя процессный подход. Общую сумму выплат за день моделируем в виде заявки, поступающей с периодичностью равной одной единице модельного времени. Сумму выплат за пройденное количество дней зафиксируем в объекте, предназначенном для статистического анализа и для построения функции плотности распределения [5, 6].
Для того чтобы проанализировать надежность страховой компании, дополнительно была создана имитация денежного входного потока по страховым премиям по полисам ОСАГО. На основании математической обработки данных сделаны выводы о сезонном характере зависимости сумм страховых премий от месяца заключения договора.
Гистограмма (рис. 4) наглядно иллюстрирует, что зимнее страхование по данному виду деятельности не пользуется таким спросом, как в период с начала весны до поздней осени. Повышенный спрос на страховой полис ОСАГО можно объяснить большим количеством приобретенных автомобилей в летний период, а также тем, что многие страхователи, особенно пенсионеры, не пользуются в зимний период автотранспортом. Максимум сумм премий и, как следствие, количество проданных страховых полисов наблюдается в июле, а минимум - в январе. Данные суммы были проанализированы по каждому месяцу, так же как и суммы выплат. Определены законы распределения, построены гистограммы и имитационные модели входящего финансового потока страховых премий для каждого месяца.
Проведенные исследования на базе данных моделей, а также проверка системы входящего денежного потока на адекватность позволили проанализировать прибыль страховой компании по данному виду деятельности.
На графике отображено распределение прибыли в течение года. Минус прибыли по данному виду страхования наблюдается в январе. Но в случае рассмотрения периода с апреля по ноябрь можно отметить серьезный скачок суммы прибыли, как в исходных данных, так и в имитации. Сумма средней ежемесячной прибыли за год составляет примерно 720 тыс. рублей. Это означает, что деятельность компании по данному страховому продукту прибыльна и средний ежемесячный доход покрывает среднюю ежемесячную сумму выплаты при ДТП. Следовательно, можно сделать вывод, что данная страховая компания надежна по данному виду страхования.
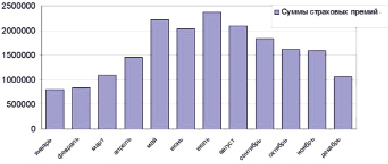
Рис. 4. Распределение сумм страховых премий за год
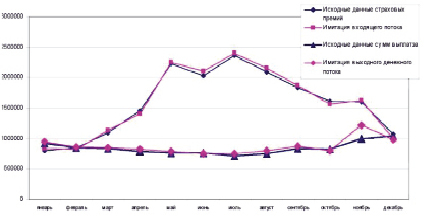
Рис. 5. Анализ прибыли, полученной по страхованию ОСАГО
Заключение
Реализована имитационная модель, поддерживающая решение задачи прогнозирования финансовых потоков выплат по договорам страхования ОСАГО. Для реализации данной системы рассмотрена деятельность страховой компании. Статистические данные о денежных выплатах при ДТП по полисам ОСАГО были собраны за 3 года.
При помощи статистических методов произведен анализ изменения потока денежных выплат в случаях ДТП. Для изучения процесса функционирования данной системы мы имели четкое представление об источниках случайных воздействий на процесс дорожно-транспортных происшествий и весьма надежные сведения об их количественных характеристиках, поэтому в нашем расчете теоретическому анализу предшествовало экспериментальное накопление статистического материала, характеризующего поведение элементов и системы в целом в реальных условиях. Обработка данного материала, а также идентификация законов распределения позволила получить исходные данные для расчета и анализа, что в дальнейшем позволило построить имитационную модель выплат.
В работе рассмотрено практическое применение методов имитационного моделирования. В прикладном пакете MS Excel реализована имитационная модель страховых выплат по полисам ОСАГО, позволяющая прогнозировать ежемесячный объем денежных средств на компенсацию ущерба по договорам страхования.
Для визуализации построенной модели применялась среда моделирования AnyLogic, при помощи которой система денежных выплат была реализована в полном размере – получено построение временных рядов в автоматическом режиме. Также на основе построенной гистограммы можно сразу определить вид распределения имитированных данных. А на основе численных экспериментов мы произвели проверку системы денежных выплат на адекватность.
Реализована имитационная модель входящего потока денежных средств на основании полученных сумм страховых премий. На основании данных имитации, зная величину входящего и выходящего потока, была проанализирована прибыль страховой компании по данному виду страхования. Из проведенного анализа можно сделать вывод, что страховая компания надежна по данному виду страхования, так как средний ежемесячный доход покрывает среднюю ежемесячную сумму выплаты при ДТП.
Работа имеет прикладное значение и содержит теоретические результаты. Полученные результаты могут быть использованы при оптимизации деятельности страховых компаний.
Библиографическая ссылка
Николаева Е.А., Карнадуд О.С., Грибанов Е.Н. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДЕНЕЖНЫХ ВЫПЛАТ ПО СТРАХОВЫМ ПОЛИСАМ ОБЯЗАТЕЛЬНОГО СТРАХОВАНИЯ АВТОГРАЖДАНСКОЙ ОТВЕТСТВЕННОСТИ (ОСАГО) // Фундаментальные исследования. – 2017. – № 8-2. – С. 286-291;URL: https://fundamental-research.ru/ru/article/view?id=41662 (дата обращения: 20.04.2024).