В последние годы универсальный язык математического моделирования используется в различных областях научных исследований. Это в большой степени связано с тем, что многие результаты исследований в различных областях не могут быть получены без использования математических моделей. Математическое моделирование и анализ систем успешно используется в химической технологии, фармакологии, физиологии, экономике, социально-гуманитарных науках с целью лучше понять и выразить количественно идеи о взаимодействиях, происходящих внутри сложных систем.
Математическая модель – это, как правило, система уравнений, описывающих, с некоторыми допущениями, процессы, происходящие внутри сложной системы. Наибольший интерес представляют собой модели кинетики, позволяющие прогнозировать изменение поведения системы с течением времени. В гуманитарных науках и экономике в качестве кинетических моделей используются временные ряды, которые позволяют адекватно описывать прошлое, но не способны дать какое-либо адекватное представление о будущем, что наиболее интересно в задачах принятия решений. В технических науках для описания кинетики, как правило, используют аппарат дифференциальных уравнений. Такие модели описывают связь между фактором и скоростью изменения отклика и обладают хорошими прогностическими возможностями.
В данной работе рассматривается одна из проблем построения дифференциальных моделей – параметрическая идентификация, иначе – отыскание параметров модели, удовлетворяющих экспериментальным данным. Эта задача относится к классу обратных задач и является некорректной (по определению Адамара). Причиной некорректности задачи параметрической идентификации является недостаток информации о процессе или системе, для которых строится модель [1].
Для учета дополнительной априорной информации в модели авторы предлагают задачу параметрической идентификации модели ставить как многокритериальную. Один из критериев будет описывать разницу между расчетными значениями и экспериментальными данными, остальные – дополнительную информацию о процессе.
В первой части статьи дается постановка задачи параметрической идентификации как однокритериальной и многокритериальной, обосновываем выбранный метод решения. Во второй части статьи приводятся результаты расчетов для дифференциальной модели кинетики реакции N-замещенных адамантилсодержащих имидоилхлоридов в реакции с фенолом в неполярном растворителе.
Постановка задачи
Как было сказано выше, основными проблемами построения дифференциальных моделей являются их структурная и параметрическая идентификация. Если представить математическую модель системы в виде
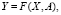(1)
где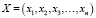 
представляет собой вектор, компонентами которого являются факторы (входные переменные), 
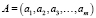– вектор варьируемых параметров системы уравнений, 
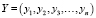– вектор откликов (выходные переменные), F – заданная векторная функция. Тогда задача структурной идентификации формулируется следующим образом.
Пусть задан набор экспериментальных данных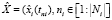 
, компонентов вектора факторов. Так же задан набор функционалов 
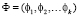, которые могут определять близость решения 
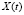набору экспериментальных данных. Необходимо найти векторную функцию 
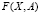, принадлежащую заданному классу функций 
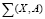, такую что
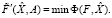(2)
Для задачи параметрической идентификации так же задан набор экспериментальных данных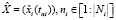 
. Определен набор функционалов 
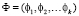и мера рассогласования:
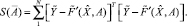(3)
Под МНК-оценкой вектора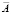 
понимается то значение вектора 
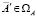при котором достигается абсолютный минимум приведенной меры:
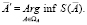(4)
Задача параметрической идентификации строится как однокритериальная задача минимизации меры рассогласования. Такая постановка задачи приводит, как правило, к существенной мультиколлинеарности. В работе [2] предложен метод добавления априорной информации в задачу на основе теории качеств. Такой подход дает хорошие результаты, но требует создания специфического программного обеспечения.
Задачу параметрической идентификации можно представить как многокритериальную, куда мера рассогласования (3) будет входить как один из критериев. Остальные критерии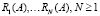 
будут формулироваться в зависимости от априорной информации.
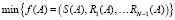. (5)
Так как не существует единого решения, которое было бы оптимальным для всех критериев, вместо него будем искать множество неулучшаемых решений, так называемую оптимальность по Парето. Неулучшаемые решения – это такой набор параметров, описывающих состояние некоторой системы, при котором значение каждого частного показателя, характеризующего систему, не может быть улучшено без ухудшения других.
Выбор лицом, принимающим решение (ЛПР), одного решения из множества основан на понимании процессов, протекающих внутри системы, и для ряда областей является субъективным [7]. Однако для моделирования технологических процессов, имеющих четкий физико-химический смысл, такой подход позволяет находить качественные значения параметров.
На данный момент разработано большое количество методов построения фронта Парето [5, 6, 8, 9]. Это различные генетические алгоритмы (moGA, nsGA, rwGA), многокритериальные градиентные методы, основанные на методах наискорейшего спуска и Ньютона, различные методы взвешенных сумм (AWS, WS). В данной работе мы остановились на методе moGA.
Выбор в качестве метода построения фронта Парето генетического алгоритма был связан с тем, что:
1) генетические алгоритмы являются достаточно простыми при реализации;
2) дают хорошие результаты на большом круге задач;
3) за один запуск возможно получить искомое приближение множества Парето.
Восстановление модели кинетики N-замещенных адамантилсодержащих имидоилхлоридов в реакции с фенолом в неполярном растворителе
В качестве практического приложения рассмотренной теории рассмотрим задачу параметрической идентификации кинетической модели реакции N-замещенных адамантилсодержащих имидоилхлоридов с фенолом. Экспериментальная часть исследования была выполнена В.А. Васильевым под руководством профессора кафедры ТОНС ВолгГТУ д.х.н. Е.В. Шишкина [3].
Было установлено, что процесс взаимодействия имидоилхлорида с фенолом протекает по следующей схеме:
В этой схеме стадия (б) подчеркивает, что при взаимодействии имидоилхлорида (Р) с фенолом возможно образование по обратимой реакции соли имидата (P•HCl). Вещества (A) и (B) – адамантилсодержащий имидоилхлорид и фенол соответственно.
Кроме двух реакций в системе протекает еще и физический процесс десорбции хлористого водорода, влияние которого на кинетику химической реакции необходимо учесть. Для этого необходимо дополнить систему кинетических уравнений уравнениями массопереноса и уравнениями диффузии части веществ к воздушным полостям в реакторе, которые и обеспечивают вынос части реагентов из зоны реакции. Однако такой способ учета влияния процесса десорбции делает задачу восстановления кинетики трудноразрешимой в вычислительном плане, поэтому было решено подобрать некоторую аналитическую зависимость, отражающую влияние фоновых физических процессов.
Для начала необходимо разобраться, в чем же выражается это влияние. Если бы мы имели дело с простой реакцией в одну стадию (а), то влияние десорбции на химический процесс выражалось бы только небольшим запаздыванием результатов на начальной стадии реакции. Однако у нас реакция в две стадии, причем вторая стадия обратимая с некоторой константой равновесия и в данном случае процесс десорбции, удаляя хлористый водород из зоны реакции, «разрывает» это равновесие. В таком случае приближенно десорбцию можно описать как некоторую псевдохимическую стадию (в), превращающую хлористый водород в некоторое нереагирующее соединение.
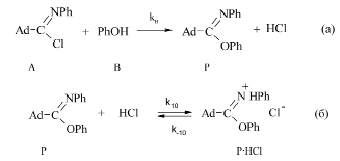
(в)
В итоге для математического описания процесса взаимодействия имидоилхлорида с фенолом (согласно закону действующих масс) нами предложена математическая модель 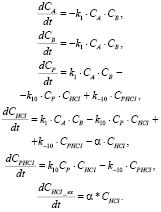(6).
(6)
Константы скорости подчиняются закону Аррениуса 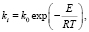(7):
(7)
где k0 и E (ккал/моль) – константы, подлежащие оценке, T – температура (К), R – универсальная газовая постоянная (ккал/(моль*K)), CA, CB, CHCl, CPHCl – концентрации реагентов (моль/л). Система дифференциальных моделей (6), описывающих кинетику химических реакций, решается для определенных начальных условий. Поскольку эксперименты проводились при различных наборах температур и начальных концентраций (как того требует методика проведения химического эксперимента), то начальные условия для удобства восприятия были сведены в табл. 1.
Экспериментальные данные были получены для нескольких серий опытов, при следующих начальных условиях (табл. 1).
В эксперименте регистрировалось изменение концентрации выдуваемого из реакционной массы хлористого водорода HCl_ex –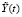 
.
Для представления задачи как многокритериальной были сформулированы две группы критериев: в первую группу входит мера рассогласования между экспериментальными и расчетными значениями концентраций HCl_ex, во вторую группу входит критерий описывающий невязку МНК оценки констант уравнения Аррениуса. Критерии первой группы были сформулированы отдельно для каждой температуры.
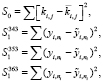
В итоге многокритериальная постановка задачи параметрической идентификации формулируется следующим образом: необходимо найти такой набор констант k для модели (6), которые позволят получить минимум ниже приведенных мер 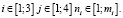(8).
(8)
Таблица 1
Начальные значения концентраций реагентов
|
Температура, K |
№ |
СA0 Имидоилхлорид (моль/л) |
СВ0 Фенол (моль/л) |
СРНl0 Имидат (моль/л) |
|
343 |
1.1 |
0,1 |
0,5 |
0,1 |
|
1.2 |
0,1 |
0,5 |
0 |
|
|
1.3 |
0,05 |
0,5 |
0,05 |
|
|
1.4 |
0,05 |
0,5 |
0 |
|
|
353 |
2.1 |
0,1 |
0,5 |
0,1 |
|
2.2 |
0,1 |
0,5 |
0 |
|
|
2.3 |
0,05 |
0,5 |
0,05 |
|
|
2.4 |
0,05 |
0,5 |
0 |
|
|
363 |
3.1 |
0,1 |
0,5 |
0,1 |
|
3.2 |
0,1 |
0,5 |
0 |
|
|
3.3 |
0,05 |
0,5 |
0,05 |
|
|
3.4 |
0,05 |
0,5 |
0 |
Таблица 2
Результаты отыскания параметров модели (6) с начальными условиями (табл. 1)
|
Температура, К |
k1 (моль/(л·с)) |
k10 (моль/(л·с)) |
k–10 (моль/(л·с)) |
|
343 |
0,198 |
48,85 |
0,0225 |
|
353 |
0,253 |
97,569 |
0,07136 |
|
363 |
0,754 |
195,2 |
0,228 |
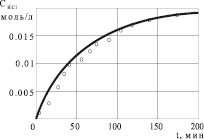
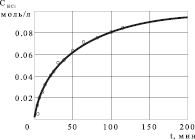
а) б)
Рис. 1. Экспериментальные (точки) и расчетные (сплошная линия) концентрации выдуваемого хлористого водорода в реакции N-замещенных адамантилсодержащих имидоилхлоридов в реакции с фенолом в неполярном растворителе: а) при 343 K, б) при 353 K
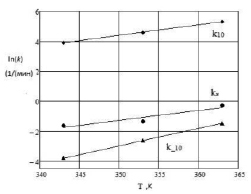
Рис. 2. Зависимости констант скоростей от температуры. •, ♦ – расчетные точки, сплошная линия – закон Аррениуса
Задача параметрической идентификации модели химической кинетики состоит в отыскании таких параметров модели, которые дают минимум невязки между экспериментальными и теоретическими данными. Поскольку мы сформулировали несколько критериев, которым должны соответствовать искомые параметры, то наша задача является задачей многокритериальной оптимизации. Одним из методов решения таких задач является построение фронта Парето с помощью различных методов (в нашем случае был использован генетический алгоритм moGA), а затем – отыскание одного решения из множества Парето оптимальных. Как правило, выбор такого решения осуществляется ЛПР на основе представлений о процессе (в данном случае физико-химическом смысле). Среди множества решений было выбрано решение, представленное в табл. 2, как наиболее близкое к решениям, полученным другими методами в работе [4].
Адекватность математической модели (7) экспериментальным данным также оценивалась по величине квадратичной ошибки отклонения, которая оказалась равной 3,57 %. Рис. 1 иллюстрирует соответствие расчетных и экспериментальных данных для температур 343 K и 353 K. Зависимость констант от температуры описывается законом Аррениуса (рис. 2). На интервале от 343 K до 363 K полученные результаты можно считать удовлетворительными.
Выводы
Исследования, проведенные в данной работе, показали, что при наличии нескольких наборов экспериментальных данных или иной дополнительной априорной информации задачу параметрической идентификации дифференциальной модели можно представить как многокритериальную. Такая оценка параметров модели является более точной, так как учитывается большее количество факторов. Выбор оптимального решения осуществляется ЛПР с учетом представлений о моделируемом процессе.
Развитые представления использовались для решения ряда прикладных задач, совместно с кафедрами химико-технологического направления ВолгГТУ. В процессе этой работы получены новые результаты, которые было невозможно получить классическими методами. Решение одной из таких задач – восстановление модели кинетики N-замещенных адамантилсодержащих имидоилхлоридов в реакции с фенолом в неполярном растворителе представлено в данной статье. Полученные результаты соответствуют результатам кинетического эксперимента, относительное расхождение экспериментальных и расчетных значений составляет 4 %. Такое качественное решение было получено за счет того, что многокритериальная постановка позволяет учесть связи между экспериментами, проводимыми при разных температурах.
Библиографическая ссылка
Тарасова И.А., Асанова Н.В., Соловьева О.Ю. МНОГОКРИТЕРИАЛЬНАЯ ИДЕНТИФИКАЦИЯ ДИФФЕРЕНЦИАЛЬНЫХ МОДЕЛЕЙ // Фундаментальные исследования. – 2017. – № 7. – С. 77-82;URL: https://fundamental-research.ru/ru/article/view?id=41588 (дата обращения: 19.04.2024).