В работе рассмотрены наиболее перспективные геометрические методы, используемые при решении задач распознавания в системах управления, когда субъективный человеческий фактор отсутствует, т.е. решение по результатам предварительной классификации и окончательного распознавания морского объекта система должна принять полностью самостоятельно.
Цель исследования
Целью научно-технических разработок авторов статьи является создание широкомасштабной радиогидроакустической системы освещения атмосферы, океана и земной коры, мониторинга их полей различной физической природы и разработка нейросетевой экспертной системы (НЭС) распознавания и классификации в общей структуре просветной системы мониторинга, включая комплекс ее автоматизированного управления. НЭС и реализующая ее система направлены на решение задач дальнего параметрического приема, измерения и распознавания пространственно-временных и спектральных характеристик, динамики гидро- и геофизических волн, формируемых неоднородностями морской среды и дна.
Материалы и методы исследования
Все геометрические методы распознавания основаны на использовании некоторой функции подобия (принадлежности) S объекта данному классу. Функция S определяет некоторую меру близости объекта bj с координатами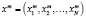 
к множеству эталонов 
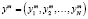. Одна из наиболее употребимых мер степени близости – среднеквадратичное отклонение (среднеквадратическое расстояние) [1, 4, 6].
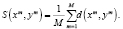(1)
Метрика измерения степени близости (расстояния) может быть разной, но должна удовлетворять условиям
d (a, b) = d (b, a); (2)
d (a, c) ≤ d (a, b) + d (b, c); (3)
d (a, b) ≥ 0; (4)
d (a, b) = 0 только при а = b. (5)
При использовании метрики типа (1) процесс обучения при геометрическом подходе можно трактовать как задачу определения такой оптимальной метрики, при которой минимизировалось бы расстояние
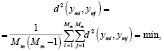(6)
где уmi – i-ый эталон m-го класса. Двойная сумма в выражении (6) делится на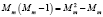 
, а не на 
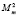, так как в соответствии с выражением (5) 
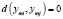при j = i.
Следует отметить, что в системах распознавания мины «Captor» и отечественной мине-торпеде ПМТ-1 использовался именно геометрический метод распознавания в самой примитивной форме [2, 8]. В системах распознавания названных изделий использовался класс метрик, который описывается формулой
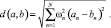(7)
Необходимо найти такие коэффициенты wn, чтобы выражение (7) стало минимальным. Физический смысл весовых коэффициентов состоит в следующем. Будем считать, что два объекта а и b представляются признаками (точками) с координатами an и bn в N-мерной ортогональной системе координат некоторого абстрактного пространства (временного, евклидова, Фурье или другого). Расстояние между точками в этом пространстве можно определить по формуле
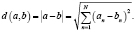(8)
Для уменьшения роли малозначащих признаков обычно вводятся нормирующие весовые коэффициенты, т.е. вместо метрики (8) используется метрика вида (7).
Обычно при геометрической трактовке распознавания образов прибегают к интерпретации процесса в виде некоторого пространственного преобразования, при котором объекты одного класса сжимаются, а множества различных классов удаляются друг от друга.
Существуют самые различные (линейные, нелинейные) методы преобразований. Например, классикой в распознавании акустических образов является преобразование временного пространства в частотные [5, 9]. Частотный метод распознавания будет выделен и рассмотрен отдельно. Если ограничиться линейным преобразованием пространства признаков объекта, то преобразование можно задать матрицей.
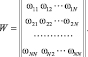(9)
Если в исходной системе координат заданы векторы объектов
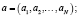
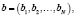(10)
то преобразованные вектора (а', b') определяют как
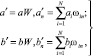(11)
а разность векторов – формулой
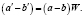(12)
Евклидово расстояние между элементами в преобразованном пространстве равно
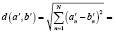
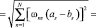
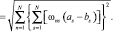(13)
Геометрический смысл этой формулы заключается в том, что сначала определяется сумма (внутренняя) взвешенных расстояний n-м признаком по всем эталонам класса, а затем – сумма (внешняя) квадратов расстояний по всем признакам, т.е. в начале производится усреднение по эталонам, потом по признакам.
Диагональные коэффициенты матрицы (9) W определяют масштабные коэффициенты сжатия вдоль координат осей. Остальные элементы матрицы определяют поворот координатных осей. Если поворота координат нет (т.е. все недиагональные элементы матрицы (9) равны нулю), то выражение (13) можно записать в виде
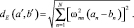(14)
В рассматриваемом случае поворот координатных осей не производится. Изменяется только масштаб вдоль координатных осей. Требуется определить такие коэффициенты сжатия, чтобы в новой системе координат расстояния между объектами множества были минимальны, т.е.
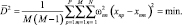(15)
Дальнейшие промежуточные выкладки приводятся только из-за их универсальности использования практически к любому частному методу геометрической постановки задачи, которыми являются большинство используемых на практике методов [4, 6, 7].
Для решения, точнее определенности, наложим в исходных параметрах ограничения на весовые коэффициенты, т.е. положим
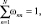(16)
или
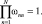(17)
Ограничение (16) требует, чтобы ωnn изменялись в пределах от 0 до 1, и их сумма равнялась единице. Ограничение (17) приводит к тому, что объемы пространства, занимаемые классами до и после преобразования равны друг другу.
Все дальнейшие рассуждения поведем для случая (16), которые в общем случае идентичны для случая (17).
Если в выражении (15) поменять порядок суммирования и ввести обозначение
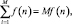(18)
то после преобразований получим
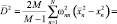
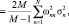(19)
где 
– некоторое дополнительное преобразование, например смещение начала координат или дисперсия.
При решении практических задач распознавания выражение (19) приводят к виду
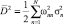(20)
и решают задачу методом Лагранжа при условии
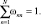
Вводя множитель Лагранжа l, сводим задачу отыскания условного экстремума к задаче поиска абсолютного экстремума, т.е. к минимизации функции вида
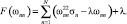
Продифференцировав по wnn и приравняв полученное выражение к нулю, получим систему из n уравнений
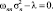(21)
Отсюда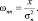 
Подставляя последнее выражение в формулу (20), получим
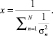(22)
Окончательно имеем
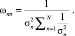(23)
Анализ выражения (23) позволяет сделать ряд важных выводов. Если дисперсия в значениях некоторого признака n = n1 эталонов рассматриваемого класса велика, т.е.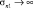 
, то этот признак можно исключить из рассмотрения, так как он ничего не дает при распознавании. Этот факт имеет вполне физическое объяснение. Если, например, при распознавании типа подводного объекта (подводной лодки) по акустическому портрету использовать цвет окраски бортов, то значение этого признака имеет такую большую дисперсию, что этот признак можно (и нужно) исключить из рассмотрения.
Наоборот, если у эталонных представителей данного класса значение определенного признака одно и то же, то этот признак имеет существенное значение. Например, у однотипных подводных объектов имеются в частотном пространстве ярко выраженные резонансные составляющие на определенных частотах (внутренние работающие механизмы, винт и др.), которые и используются как наиболее весомые признаки.
Если решать задачу (17), т.е. требовать сохранения объема пространства, то получается задача на условный экстремум:
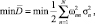(24)
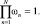(25)
Вводя множители Лагранжа, получим
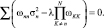(26)
Используя выражения (24), получим
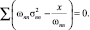(27)
Отсюда
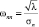(28)
или
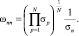(29)
Из выражения (29) следует, что весовой коэффициент данного признака обратно пропорционален среднеквадратическому значению данного признака, т.е. можно считать, что при большом N сумма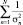 
в выражении (23) и произведение 
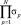в выражении (29) постоянны.
В обоих случаях, определяемых формулами (23) и (29), весовые коэффициенты могут рассматриваться как грубое описание класса. Если классов несколько, то весовые коэффициенты находятся для каждого класса. Общее решающее правило в задачах геометрического распознавания формулируется следующим образом. Пусть даны два класса А1 и А2. Для распознавания принадлежности некоторого объекта р к классу {xm} определяется величина
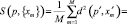
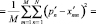
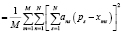. (30)
Решающее правило функционирования распознающего устройства на основании выражения (30) состоит в следующем:
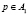; если 
;
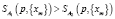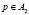; если 
,
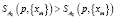причем в каждой из функций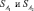 
коэффициенты ans ищутся применительно к первому или второму множеству эталонов. Метод имеет три модификации: метод потенциальных функций, метод решающих функций, метод дискриминантных функций.
Результаты исследования и их обсуждение
Глобальная идея фактически одна и заключается в следующем. Считается априори, что существуют поверхности условных плотностей распределения вероятностей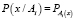 
, т.е. вероятностей появления значений признака х при условии, что объект принадлежит классу Аi. Однако сформировать алгоритм, описывающий эту функцию, и запомнить в точном виде довольно затруднительно даже для специализированной электронно-вычислительной машины. Обычно поверхности условных плотностей распределения вероятностей, представляющих многомерную функцию высокого порядка, аппроксимируют какими-нибудь функциями, которые называют решающими, потенциальными или дискриминантными функциями gi(x). Как правило, аппроксимирующие функции значительно проще в математическом представлении. Причем практически задача заключается не столько в аппроксимации, сколько в методике построения этих функций, если заданы какой-то набор эталонов или обучающая последовательность.
Обычно функции выбираются таким образом, чтобы облегчить процесс их практического получения. Эта постановка задачи характерна для вероятностного распознавания. При детерминированном распознавании задается некоторое количество (а не функций распределения вероятностей) и требуется любой новый объект отнести к определенному классу. Здесь предполагается существование разделительных поверхностей. Аналогичным образом на этом множестве эталонов определяются дискриминантные функции gi(x). Разделительные поверхности определяются из уравнений
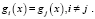(31)
В методе дискриминантных функций выбирают другое выражение (модуль и знак разности)
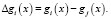(32)
Если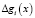 
положительное, то объект относят к классу i, если отрицательное – к классу j.
В качестве пояснений рассмотрим пример классификации некоторого набора подводных объектов по шумовому портрету. Всего распознается m типов лодок. Каждый тип объекта задан в распознающем устройстве набором эталонов М1, М2, … , Мm. Каждому типу (классу) ставится в соответствие потенциальная функция
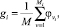(33)
где
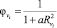(34)
– потенциал, приписываемый n-му объекту i-го класса.
Функционал (34) графически представим в виде кривой (потенциальной функции). По этой формуле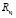 
– это расстояние от точки с координатами n-го эталона в i-м классе до любой другой рассматриваемой точки. Термин «потенциальная функция» связан базовыми понятиями электрических или гравитационных полей, что весьма удобно, исходя из следующих рассуждений. Если в пространстве эталонов в точках, где размещаются эталоны, разместить электрические заряды (или гравитационные массы), то каждый из зарядов создаст вокруг себя поле с потенциалом
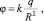(35)
где q – величина заряда; k – коэффициент пропорциональности (вес); R – расстояние от заряда.
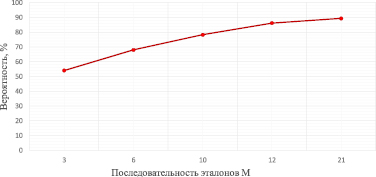
Кривая обучения при исследовании с распознаванием цифр
Если зарядов (эталонов) несколько, в сумме функции (35) дадут какую-то потенциальную поверхность. Рассматриваемая задача известна в литературе. Например, в работе [7] приводятся исследования по распознаванию десяти цифр (0, 1,…, 9) с помощью метода потенциалов. На рисунке представлена кривая обучения, полученная в результате исследований с распознаванием цифр.
В работе [3] приводится методика и ее реализация по распознаванию сорока критериев состояния Мирового океана с помощью оптического сканера, установленного на спутнике. На рисунке по оси абсцисс отложено тело эталонных изображений, предъявленных в процессе обучения. Начиная с М = 13 при значениях Р = 85 % кривая вероятности (или надежности) распознавания идет практически параллельно оси абсцисс. Это явление объясняется тем, что к данному числу предъявлений система уже освоила процесс распознавания.
Вторым объяснением могут быть следующие рассуждения. Пусть распознаванию подлежат два класса (а и b). Имеется набор эталонов, представляющих эти классы. Если речь идет о «полном» представлении, то точки эталонов располагались бы равномерно в пространстве образов. Но это довольно редкий случай. Чаще встречается ситуация, когда в одном участке бывает сгущение точек, а в другом – разрежение. Если сгущение в одной подобласти расположено вблизи разрежения другой, то возможны ошибки в классификации (в точках пересечения областей признаков классов).
Для улучшения процесса распознавания необходимо устранить несколько циклов обучения. Когда оканчивается первый цикл обучения, распознающее устройство вторично обучает на тех же эталонах. При этом появляются ошибки (например, уже описанные) и распознающее устройство доучивается. При повторном обучении увеличивают веса (потенциалы) точек распознанных ошибочно (величина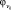 
в формуле (35)), а число М в той же формуле оставляют неизменным. Циклы обучения повторяются до тех пор, пока распознавание будет полностью правильным. Исследования показали, что если при простейшем алгоритме последовательность эталонов N увеличится с 12 до 21, то вероятность распознавания десяти категорий будет одинакова и равна Р = 85 %. При улучшенном алгоритме распознавания для N = 12 при значениях Р = 86,1 %, а для N = 21 при значениях P = 89,3 %.
Выводы
Рассмотренные методы наиболее перспективны в решении задач распознавания в системах управления, когда субъективный человеческий фактор отсутствует, т.е. решение по результатам предварительной классификации и окончательного распознавания система должна принять полностью самостоятельно, в частности в линиях классификации нейросетевой экспертной системы (на базе традиционных и нечетких нейронных сетей), входящей в состав разрабатываемой авторами широкомасштабной радиогидроакустической системы мониторинга полей источников атмосферы, океана и земной коры [9].
Библиографическая ссылка
Пятакович В.А., Василенко А.М. ПЕРСПЕКТИВЫ И ОГРАНИЧЕНИЯ ИСПОЛЬЗОВАНИЯ ГЕОМЕТРИЧЕСКИХ МЕТОДОВ РАСПОЗНАВАНИЯ АКУСТИЧЕСКИХ ОБРАЗОВ МОРСКИХ ОБЪЕКТОВ ПРИМЕНИТЕЛЬНО К ЗАДАЧЕ УПРАВЛЕНИЯ НЕЙРОСЕТЕВОЙ ЭКСПЕРТНОЙ СИСТЕМОЙ // Фундаментальные исследования. – 2017. – № 7. – С. 65-70;URL: https://fundamental-research.ru/ru/article/view?id=41586 (дата обращения: 26.04.2024).