Основной задачей нашего исследования являлась проверка предположения, что все физические свойства металлических сплавов взаимосвязаны. Поэтому можно найти корреляционные уравнения, связывающие различные свойства между собой. Имея корреляционные уравнения и изучив подробно одно из физических свойств сплавов, мы можем прогнозировать, как будут изменяться остальные свойства в зависимости от изменения концентрации одного из легирующих элементов или при замене этого элемента на другой. Проверка выдвинутого нами предположения производилась для бинарных сплавов на основе алюминия в области твердых растворов. Бинарные сплавы были выбраны потому, что для них существует достаточно много экспериментальных данных.
Развитие современной техники предъявляет все более высокие требования к материалам [1–3]. Стандартные литейные и деформируемые сплавы на основе алюминия часто не отвечают этим требованиям, что вынуждает использовать более дорогие материалы, в частности полученные по специальным технологиям (сверхбыстрая кристаллизация, механическое легирование, замешивание в расплав ультрадисперсных частиц и т.д.). Высокая стоимость последних существенно ограничивает производство и потребление готовых изделий [4, 5].
Обычный метод улучшения потребительских свойств традиционных сплавов связан с легированием. Оно производится, как правило, эмпирическим путем, что в свою очередь требует большого экспериментального поиска, для которого необходима огромная затрата средств, времени и значительных усилий научных работников различных профессий: металлургов, химиков, металлофизиков.
В связи с вышесказанным представляется актуальным создание такого теоретического метода, который позволял бы расчетными методами определять свойства еще не изученных до этого сплавов, исходя из ограниченного экспериментального материала и являясь при этом не очень сложным с математической точки зрения.
В настоящее время в квантовой химии создан ряд методов, позволяющих производить расчеты электронной структуры вещества [6], но, к сожалению, эти методы очень сложны с математической точки зрения даже для простейших систем, а для многокомпонентных сплавов они практически неприменимы. В работах [7–12] рассматриваются некоторые методы расчета взаимодействия и стабильности фаз. В этих расчетах величины межатомного взаимодействия являются феноменологическими параметрами и либо берутся из эксперимента по фазовым равновесиям в сплавах, либо подбираются таким образом, чтобы обеспечить удовлетворительное согласие теории с опытными данными. Существенным недостатком такого подхода является невозможность прогнозирования свойств новых материалов по этим параметрам.
Учитывая вышесказанное, авторы в своих исследованиях приступили к созданию теории, которая была бы несложной с математической точки зрения и одновременно с этим позволяла бы прогнозировать свойства еще не изученных сплавов. Исходным пунктом исследования было предположение, что некоторые свойства трехкомпонентных сплавов можно выразить через свойства бинарных сплавов. В работах [10] и [11] было показано, что молярные объемы и объемы смешения трехкомпонентных никелевых сплавов можно выразить через соответствующие молярные объемы и объемы смешения двухкомпонентных сплавов. В работе [10] была произведена проверка справедливости этого утверждения для энтальпии смешения. В этом же исследовании показано, что вышеприведенные свойства для четырех, пяти и т.д. компонентных сплавов можно выразить через свойства бинарных сплавов. Ограничением в развитии этого направления является тот факт, что из всего многообразия физических свойств металлических сплавов только немногие можно выразить через свойства бинарных сплавов.
Для преодоления этого недостатка было выдвинуто предположение, что все физические свойства сплавов взаимосвязаны между собой, так как они определяются атомной структурой вещества. Поэтому возможно построение корреляционных уравнений между различными свойствами металлических сплавов. Пользуясь выявленными зависимостями, можно, подробно изучив одно из свойств, определить остальные свойства, опираясь на ограниченное число экспериментальных данных. Наряду с этим возможно прогнозирование свойств еще не изученных сплавов.
Для проверки вышеприведенной гипотезы авторы решили выявить взаимосвязи между различными физическими свойствами бинарных металлических сплавов на основе алюминия в области твердых растворов. Выбор на бинарные сплавы пал потому, что они исследованы более подробно, чем сплавы с более сложным составом, это дает возможность оперировать большим числом экспериментальных данных.
В своем исследовании авторы проанализировали следующие свойства веществ: твердость по Бринеллю – HB, кг/мм2, твердость по Виккерсу – Hν, кг/мм2, микротвердость – Hμ, кг/мм2, предел прочности – σв, кг/мм2, относительное удлинение – δ, %, относительное сужение – ψ, %, предел текучести – στ, кг/мм2, модуль нормальной упругости – E, кг/мм2, удельное электросопротивление – ρ, мкОм/см, теплопроводность – λ, кал/см·с, электропроводность – ρ, См.
В данной работе приведены данные по анализу следующих свойств: твердость по Бринеллю, предел прочности, относительное удлинение.
Оказалось, что в области твердых растворов все эти величины меняются линейно с ростом концентрации легирующего элемента. Математически это можно описать следующим уравнением:
Y = α+ bx, (1)
где Y – величина изучаемого свойства, α и b – коэффициенты, х – концентрация легирующего элемента. Коэффициент α показывает величину исследуемого параметра при нулевой концентрации легирующего элемента, а коэффициент b – быстроту изменения данного параметра при изменении концентрации легирующего элемента. Соответственно, при замене одного легирующего элемента на другой изменяется величина b, а коэффициент α остается неизменным. На графике зависимости свойство – концентрация, для различных легирующих элементов, мы получим набор прямых линий, расходящихся под разными углами из одной общей точки.
Использование коэффициента b вместо уравнения (1) позволяет существенно упростить поиск взаимосвязей между различными физическими свойствами сплавов, т.к. в этом случае нужно оперировать набором коэффициентов, а не набором уравнений.
Следующим этапом исследований было выявление зависимости коэффициентов b от положения легирующих элементов в таблице Д.И. Менделеева. Обработав большой массив данных, авторы обнаружили, что между коэффициентами b и номерами групп элементов n (при фиксированном номере периода N) существует взаимосвязь, но она в редких случаях носит линейный характер. В то же время зависимость между коэффициентами b и номером периода N, для легирующих элементов, принадлежащих к одной группе n, в большинстве случаев была линейной.
Далее, на основе обнаруженных закономерностей была выдвинута гипотеза, что между коэффициентами b, ответственными за различные физические параметры, может существовать корреляционная взаимосвязь. Выявив эту взаимосвязь, можно осуществлять переход от одного физического свойства к другому. Соответствующие корреляционные уравнения позволяют, подробно изучив некоторые легко измеримые свойства металлических сплавов, переходить к другим свойствам, для измерения которых используются дорогостоящие методы.
Опираясь на выявленные закономерности, можно прогнозировать свойства еще не изученных сплавов. Причем прогноз будет не только качественным, но и содержать конкретные физические величины.
Методика эксперимента
Для выявления искомых закономерностей были обработаны данные по бинарным сплавам на основе алюминия. В случае, когда данные были представлены в графическом виде, измеряли тангенс угла наклона прямой на графике состав – свойство. Тангенс угла наклона соответствует коэффициенту b уравнения (1). Если данные были представлены в виде таблицы, то для вычисления коэффициента b использовался разностный метод. Далее построили зависимости коэффициентов b от номера и периода расположения легирующего элемента в периодической системе Д.И. Менделеева и получили линейные закономерности. Обнаружив линейные закономерности, далее находили корреляционные взаимосвязи между изменением различных свойств алюминиевых сплавов и опять получили линейные зависимости. Эти корреляции позволяют прогнозировать, как будут влиять пока еще не исследованные элементы на те или иные свойства сплавов, по влиянию уже исследованных свойств легирующих элементов. Выявленные закономерности описывали математическими уравнениями. В дальнейшем, методами корреляционного анализа были выявлены взаимосвязи между изменениями различных свойств в анализируемых системах.
Корреляция между изменениями свойств алюминиевых сплавов в зависимости от вида легирующих элементов
Часто при добавлении примеси, улучшающей одно свойство сплава, наблюдается изменение других свойств, не всегда положительное. Найдем корреляцию между найденными коэффициентами, т.е. между свойствами сплавов, что даст нам возможность прогнозировать изменение одного свойства сплава, если мы знаем, как изменилось другое, при добавлении в сплав примесного элемента.
Построим график корреляции между твердостью по Бринеллю HB (b) и пределом прочности σв (b1) для сплавов на основе алюминия. Мы знаем, что чем тверже сплав, тем прочнее материал. Подтвердим это графиком зависимости коэффициента b от коэффициента b1 (рис. 1). Данные коэффициенты взяты соответственно из уравнений (2) и (3).
HB = HB0 + bх, (2)
σв = σ0 + b1х. (3)
Величины этих коэффициентов приведены в табл. 1.
Таблица 1
Значения коэффициентов b и b1 для сплавов на основе алюминия
|
Примесь |
b (твердость по Бринеллю), кг/мм2 |
b1 (предел прочности), кг/мм2 |
|
Li |
0,09 |
0,05 |
|
Cu |
0,14 |
0,22 |
|
Ag |
0,15 |
0,48 |
|
Be |
0,7 |
0,9 |
|
Pb |
0,65 |
0,28 |
Как видно из графика (рис. 1), наблюдается существенный разброс точек, но если мы обратим внимание на то, какие элементы взяты для построения графика, то увидим, что из пяти выбранных элементов три относятся к первой группе, а остальные – соответственно ко второй и четвертой группе элементов. Построение показывает, что три нижних точки на графике соответствуют элементам первой группы, а две верхних – остальным элементам. Поэтому на графике прямая линия должна проходить через три нижние точки, а оставшиеся точки можно считать выбросом. Вновь подтверждается ранее замеченное правило: линейные зависимости между свойствами сплавов характерны для элементов, принадлежащих к одной группе.
Полученное уравнение (рис. 1) соответствует уравнениям (2) и (3).
Найдем взаимосвязь между коэффициентами b и b2, то есть между твердостью по Бринеллю HB и относительным удлинением δ для систем на основе алюминия. Коэффициенты b и b2 взяты соответственно из уравнений (2) и (4). Величины этих коэффициентов приведены в табл. 2.
δ = δ0 + b2х. (4)
Таблица 2
Значения коэффициентов b и b2 для примесей сплава на основе алюминия
|
Примесь |
b (твердость по Бринеллю), кг/мм2 |
b2 (относительное удлинение), % |
|
Li |
0,05 |
0,15 |
|
Cu |
0,22 |
0,09 |
|
Si |
0,24 |
0,08 |
|
Mg |
0,35 |
0,05 |
|
Ag |
0,48 |
0,03 |
|
Ca |
0,72 |
0,02 |
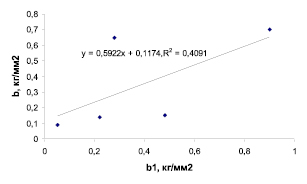
Рис. 1. Зависимость коэффициента b от коэффициента b1
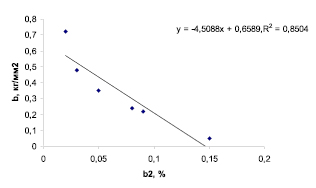
Рис. 2. Зависимость коэффициента b для сплавов алюминия от коэффициента b2
Основываясь на этих данных, строим график зависимости между коэффициентами b и b2 (рис. 2).
Уравнение, связывающее коэффициенты b2 и b, выглядит следующим образом:
b = 0,6589 – 4,5088b2, (5)
причем достоверность аппроксимации R2 = 0,85. Как видно из уравнения (5), мы можем, зная относительное удлинение и, соответственно, коэффициент b2 для некоторого легирующего элемента введенного в алюминиевые сплавы, вычислить коэффициент b, а от него перейти к твердости по Бринеллю HB. Соответственно, мы можем вычислить твердость по Бринеллю HB для всех сплавов в области твердых растворов для данного легирующего элемента. Действуя подобным образом, мы можем определить твердость по Бринеллю для любых легирующих элементов, относящихся к одной группе.
Вид уравнения, полученного на рис. 2, соответствует виду уравнения (5).
Далее в своей работе авторы выявили корреляционные взаимосвязи между тангенсами угла наклона для модуля нормальной упругости и тангенсом угла наклона температуры ликвидуса, между изменением предела прочности и изменением ликвидуса и еще ряд корреляционных зависимостей для различных физических величин. Они не приводятся ввиду большого объема информации.
Выводы
1. В ходе работы проанализировали влияние различных примесей на изменения свойств алюминиевых сплавов в зависимости от вида легирующих элементов и соответствующего расположения этих элементов в периодической системе Д.И. Менделеева.
2. Были выявлены корреляционные взаимосвязи между изменениями различных свойств алюминиевых сплавов в зависимости от вида примеси. На основании полученных данных построены соответствующие уравнения, которые показали, что практически между всеми изученными нами физическими свойствами существует корреляционная зависимость, но в одних случаях связь довольно слабая, она позволяет только прогнозировать тенденцию в изменении того или иного свойства. В других случаях взаимосвязь такая, что позволяет вычислять, как одно свойство меняется, при изменении другого свойства.
3. Все вышеприведенное позволяет утверждать, что найдена методика, которая позволяет прогнозировать изменение физических свойств бинарных сплавов при замене одного легирующего элемента на другой. Опираясь на полученные взаимосвязи, можно теоретически предсказать свойства еще не изученных сплавов, не прибегая к эксперименту, что позволяет экономить материальные и финансовые ресурсы.
Библиографическая ссылка
Леонов В.В., Никифоров А.Г., Ковалева А.А. ВЫЯВЛЕНИЕ КОРРЕЛЯЦИОННЫХ ВЗАИМОСВЯЗЕЙ МЕЖДУ ФИЗИЧЕСКИМИ СВОЙСТВАМИ АЛЮМИНИЕВЫХ СПЛАВОВ // Фундаментальные исследования. 2017. № 7. С. 44-48;URL: https://fundamental-research.ru/ru/article/view?id=41582 (дата обращения: 17.11.2025).



