Математическая модель артериального русла служит для объединения модели глобальной гемодинамики (0D модель) и модели локальной гемодинамики церебральной артерии (3D) [1, 3, 5]. В разработанной модели гемодинамики артериального русла (1D модель) артерии большого круга кровообращения описываются совокупностью квазиодномерных артерий [3]. В отличие от модели глобальной гемодинамики [4], решение уравнений математической модели гемодинамики артериального русла сопряжено со значительными вычислительными трудностями. Исходя из размерности задачи и требуемых вычислительных ресурсов, для расчета уравнений модели артериального русла перспективным является использование технологии высокопроизводительных вычислений NVIDIA CUDA. Технология предполагает расчет уравнений математической модели не на центральном процессоре, а на специальном графическом ускорителе или видеокарте, поддерживающей технологию NVIDIA CUDA, что позволяет значительно увеличить скорость расчета уравнений математической модели гемодинамики [2].
Целью работы является разработка эффективного вычислительного метода решения уравнений математической модели гемодинамики артериального русла.
Материалы и методы исследования
Структура модели артериального русла подробно описана в [3]. В модели каждая артерия представляется совокупностью элементарных участков. Рассмотрим представление сосуда в модели артериального русла (рис. 1).
В квазиодномерном представлении i-ый сосуд длиной Li разбивается на ni элементарных участков длиной dl:
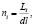
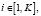 (1)
(1)
где ni – количество элементарных участков в i-ом сосуде; Li – длина i-ого сосуда, см; dl – длина элементарного участка сосуда, см; K – общее количество сосудов в квазиодномерной модели артериального русла.
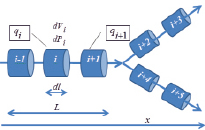
Рис. 1. Схематическое изображение бифуркации сосуда
Элементарный участок сосуда характеризуется элементарным объемом крови dV и давлением dP внутри него. Связь между i-ым и i – 1-ым элементарными участками характеризуется объемным кровотоком 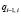 между ними.
между ними.
Для элементарного объема dVi, согласно закону сохранения массы, можно записать
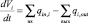 , (2)
, (2)
где 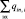 – сумма объемных кровотоков входящих в i-ый элементарный участок, см3;
– сумма объемных кровотоков входящих в i-ый элементарный участок, см3; 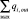 – сумма объемных кровотоков, выходящих из i-ого элементарного участка, см3.
– сумма объемных кровотоков, выходящих из i-ого элементарного участка, см3.
Для давления dPi в элементарном участке может быть принято допущение о линейной зависимости между элементарным объемом dVi и давлением dPi:
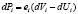 , (3)
, (3)
где dUi – ненапряженный объем (стенки сосуда не растянуты) i-ого участка элементарного сосуда, см3; еi – эластичность стенки i-ого участка элементарного сосуда, см3/Торр.
Для определения объемного кровотока qi можно использовать закон Пуазейля:
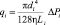 , (4)
, (4)
где η – коэффициент динамической вязкости крови; di – диаметр i-ого элементарного участка сосуда, cм.
При моделировании движения крови в аорте отдельно следует учесть, что течение крови в данном участке сердечно-сосудистой системы имеет значительное ускорение. Для учета инерционности крови уравнение (4) записывается в виде
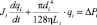 , (5)
, (5)
где Ji – инерционность крови, Торр•с2/см3.
Таким образом, используя уравнения (1)–(5) можно описать движение крови по одномерному артериальному руслу.
Результаты исследования и их обсуждение
Преобразуем систему уравнений (1)–(5) путем подстановки выражений для неизвестных величин:
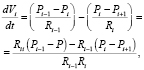
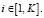
Раскроем скобки и сгруппируем элементы:
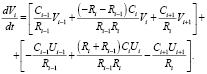
Запишем полученное уравнение в матричной форме:
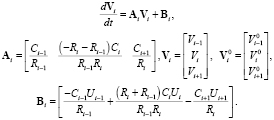 (6)
(6)
Распространяя представленный подход на совокупность элементарных участков выбранного сосуда, получим систему уравнений вида
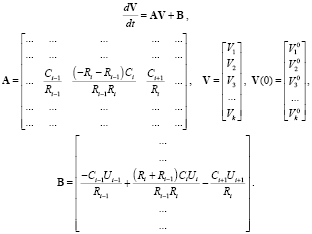 (7)
(7)
Для корректного описания модели гемодинамики артериального русла (1D модели) требуется задание соответствующих граничных условий на краевых участках артериальной системы. В разработанной модели неизвестными величинами на границах артериального русла являются 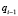 и
и 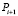 . Значения этих граничных условий могут быть получены при использовании разработанной ранее модели глобальной гемодинамики (0D модели). Таким образом, для входного участка артериального русла, при заданном значении q0, справедливо уравнение
. Значения этих граничных условий могут быть получены при использовании разработанной ранее модели глобальной гемодинамики (0D модели). Таким образом, для входного участка артериального русла, при заданном значении q0, справедливо уравнение
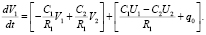 (8)
(8)
Для выходного (терминального) участка артериального русла, при заданном значении 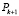 , справедливо уравнение
, справедливо уравнение
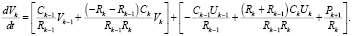 (9)
(9)
Для элементарных участков сосуда, описывающих бифуркации (например, участок i + 1 на рис. 1), обозначим x – первый участок первого сосуда после бифуркации; y – первый участок второго сосуда после бифуркации. Тогда для участка I + 1 можно записать
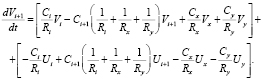 (10)
(10)
Для модели гемодинамики артериального русла был разработан эффективный вычислительный метод решения уравнений модели (6)–(10), использующий параллельную обработку данных и реализованный с помощью технологии высокопроизводительных вычислений на графическом процессоре NVIDIA CUDA (рис. 2), включающий следующие этапы:
1. Ввод данных о длительности моделируемого периода времени, шагах дискретизации по времени и длине сосуда, структуре артериального русла и характеристиках артерий.
2. Разбиение артерий на элементарные участки и вычисление ненапряженного объема, сопротивления и эластичности каждого участка.
3. Формирование матрицы коэффициентов и векторов параметров. В качестве начальных условий для объема элементарного участка артериального русла используется значение его ненапряженного объема. Граничные условия на входе и выходе из артериального русла определяются в соответствии со значениями параметров глобальной гемодинамики.
4. На графическом процессоре предварительно выделяется память, необходимая для хранения расчетных данных, и производится копирование данных из RAM в GDRAM.
5. Для каждого временного шага производится параллельный расчет с использованием Θ вычислителей. Для этого матрица коэффициентов и векторы параметров разбиваются на подматрицы, для каждой из которых происходит обработка в параллельном режиме, определяется вектор объемов элементарных участков и производится пересчет вектора сопротивлений элементарных участков.
6. Синхронизация всех вычислительных потоков для обеспечения целостности данных.
7. Определение новых значений элементов для матрицы коэффициентов и вектора параметров в соответствии с функциональным назначением элементарных участков.
8. Копирование вектора объемов элементарных участков из GDRAM в RAM и обработка результатов расчета.
9. Переход на следующий временной шаг. Процесс расчета повторяется, пока не буден смоделирован весь заданный период времени.
10. Сохранение значений в базе данных и вывод графиков изменения объема, объемного кровотока, давления и поперечного сечения выбранных элементарных участков сосудов артериальной системы.
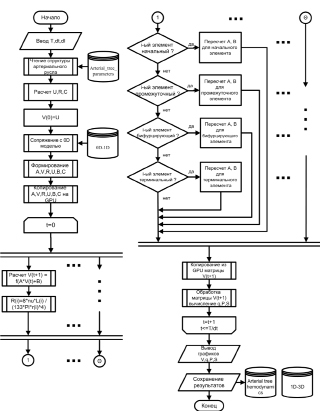
Рис. 2. Схема метода решения уравнений модели гемодинамики артериального русла
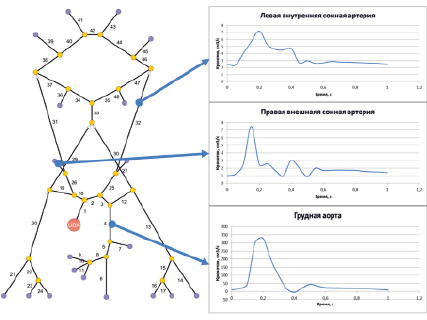
Рис. 3. Пример результатов расчета модели гемодинамики артериального русла
На языке программирования C++ разработано соответствующее программное обеспечение для расчета математической модели гемодинамики артериального русла (1D модель), использующее технологию высокопроизводительных вычислений NVIDIA CUDA. Запуск программного обеспечения осуществлялся на рабочей станции (HP Z640 E5-2620v3, 32GB DDR4-2133 (4x8GB), NVIDIA Quadro K4200 (4GB), 1TB SATA 7200 HDD). В качестве графического ускорителя использовался NVIDIA Quadro K4200.
Моделируемый период времени T составил 5 мин; шаг по длине сосуда dl = 1•10–4 м.; шаг по времени dt = 1•10–4 с. Выбранные шаги дискретизации обеспечивают сходимость разработанного метода. Пример результата расчета математической модели гемодинамики артериального русла приведен на рис. 3. Время расчета уравнений математической модели гемодинамики артериального русла при последовательной реализации предложенного вычислительного метода составило 4 часа 12 минут. Для проверки эффективности разработанного вычислительного метода решения уравнений модели гемодинамики артериального русла, результаты расчета модели с использованием графического ускорителя были сравнены с результатами расчета модели с использованием центрального процессора. При использовании предложенного вычислительного метода, использующего технологию высокопроизводительных вычислений NVIDIA CUDA, время расчета уравнений математической модели гемодинамики артериального русла было существенно снижено и составило около 22 минут (ускорение приблизительно в 12 раз). Таким образом, можно заключить, что предложенный вычислительный метод решения уравнений математической модели гемодинамики артериального русла является эффективным и позволяет сократить затраты машинного времени при расчете модели гемодинамики артериального русла в среднем в 10–12 раз.
Заключение
Разработан и реализован эффективный вычислительный метод решения уравнений модели гемодинамики артериального русла, отличающийся параллельной обработкой данных с использованием современной технологии высокопроизводительных вычислений NVIDIA CUDA.
Работа выполнена при финансовой поддержке DAAD (German Academic Exchange Service) по программе «Михаил Ломоносов» и в рамках госзадания по проекту № 18.706.2016/ДААД.
Библиографическая ссылка
Синдеев С.В., Фролов С.В. ПАРАЛЛЕЛЬНЫЙ МЕТОД РАСЧЕТА МОДЕЛИ АРТЕРИАЛЬНОГО РУСЛА ДЛЯ МНОГОМАСШТАБНОГО МОДЕЛИРОВАНИЯ ЦЕРЕБРАЛЬНОЙ ГЕМОДИНАМИКИ // Фундаментальные исследования. 2017. № 5. С. 66-71;URL: https://fundamental-research.ru/ru/article/view?id=41509 (дата обращения: 01.07.2025).



