В продолжение проработки вопросов применения электромеханических приводов (ЭМП) в управляющих контурах малоинерционных объектов регулирования [6,7] рассмотрены результаты моделирования в сравнении с результатами испытаний натурного ЭМП. Предложенная ранее совместная модель ЭМП и гидравлического блока регулирования в составе контура регулирования давления и частоты вращения паровой турбины показала свою адекватность, необходимо продолжение исследования.
Целью исследования является разработка новой модели высокоточного быстродействующего следящего электромеханического привода.
Материалы и методы исследования
В рамках исследования динамических процессов в контуре системы автоматического регулирования паровой турбины ранее было выполнено:
– рассмотрены способы обеспечения высокоскоростных линейных перемещений с прецизионным позиционированием рабочего органа – паровпускного регулирующего клапана, и выделены преимущества ролико-винтовой пары [6];
– предложена математическая модель следящего электромеханического привода, конструктивно способного с заданной скоростью и точностью управлять положением промежуточного усилительного элемента – отсечного золотника в составе исполнительного гидравлического механизма (блока регулирования) паровой турбины [7].
Рассмотренная математическая модель ЭМП составлена по опытному образцу привода, спроектированному и изготовленному ЗАО «Диаконт» (г. С.-Петербург) [8] для применения в энергетике, в т.ч. в системах регулирования частоты вращения паровых турбин ОАО «КТЗ» (г. Калуга). Характерной особенностью их является применение гидравлического исполнительного механизма – гидромеханического блока регулирования – для управления положением паровпускных регулирующих клапанов парораспределения турбины [2, 3]. Ход клапанов определяет расход свежего пара на турбину (рис. 1), однако действующие при этом паровые усилия имеют непостоянный, циклический и даже зачастую знакопеременный характер (рис. 2), что и определяет, главным образом, максимальную нагрузку на исполнительные органы блока регулирования в момент отрыва клапана от своего седла. Такое распределение усилий, которые необходимо преодолевать, по возможности, плавно – без рывков, в свою очередь, и обуславливает применение в его конструкции промежуточного усилительного звена – гидравлического отсечного золотника под управлением своего ЭМП.
Таким образом, рассматриваемый следящий привод входит в состав блока регулирования системы автоматического регулирования паровой турбины (САР ПТ), предназначенного для преобразования электрического сигнала управления от электронной управляющей части (ЭУЧ) САР ПТ, в перемещение сервомоторов (СМ), создающих необходимое усилие для перемещения регулирующих клапанов (РК).
Технические требования к функционалу современных контуров автоматического регулирования теплофизических параметров турбины, таких как давление свежего пара или частота вращения ротора, определяют достаточно высокие требования и к комплектующему их оборудованию. Как из расчётного обоснования [3], так и из практического опыта эксплуатации можно утверждать, что для контуров рассматриваемого типа (электрогидравлические) достаточным для обеспечения качественной и безопасной работы будет применение ЭМП со следующими характеристиками:
– постоянная времени (перемещение на полный рабочий ход при максимальном входном управляющем сигнале – важный компонент противоразгонной защиты турбоагрегата) – не более 0,1 сек;
– погрешность позиционирования – не более 0,1 мм;
– развиваемое усилие – не менее 1 кН.
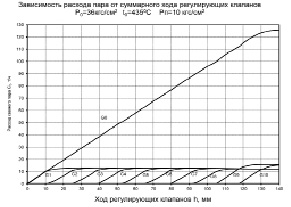
Рис. 1. Пример зависимости расхода пара на турбину по мере открытия регулирующих клапанов
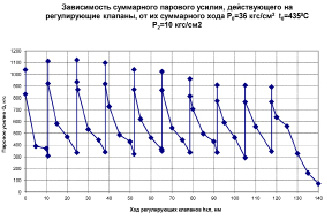
Рис. 2. Пример зависимости парового усилия, действующего на регулирующие клапаны, по мере их открытия
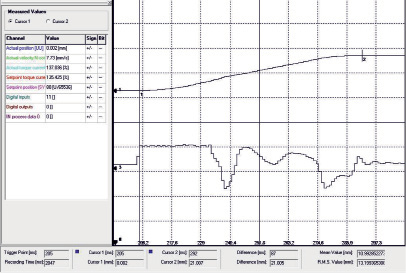
Рис. 3. Форсированное перемещение штока ЭМП на рабочий ход в мм, где метки «1» и «2» указывают на, соответственно, начало и конец перемещения
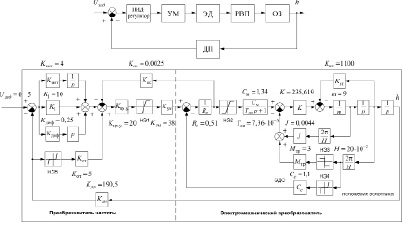
Рис. 4. Функциональная и структурная схемы следящего привода отсечного золотника, со следующими условными обозначениями: УМ – усилитель мощности, ЭД – электродвигатель, РВП – ролико-винтовая передача, ОЗ – отсечной золотник, ДП – датчик положения
При этом следует понимать, что указанные величины достаточно условны и осреднены по рабочему диапазону, т.к. в каждом конкретном случае они не только зависят от конкретных требований к качеству работы всего контура регулирования, но и сами влияют на его качество (точность и быстродействие) в существенной степени. Отсюда, помимо теоретической задачи синтеза оптимального регулирования, возникает и более практическая, инженерная задача – на этапе проектирования контура подобрать из существующего типоразмерного ряда ЭМП с такими параметрами быстродействия и точности, чтобы контур в целом смог удовлетворить по ним требованиям ТЗ.
Не рассматривая здесь первую часть задачи (методам её решения, в т.ч. и в нелинейной постановке, посвящено значительное количество работ, к примеру, [5]), уделим внимание практическим вопросам подбора и проверки необходимого оборудования, а также подтверждения параметров ранее разработанной математической модели привода [6–8].
В обеспечение решения данной задачи и в целях верификации модели ЭМП [7, 8] изготовителем отечественных образцов ЭМП данного типа (ЗАО «Диаконт», [1]) на образце типа EMD-100 (300) был проведен ряд функциональных испытаний по программам [4], в т.ч. проверкам подвергалась:
– работоспособность ЭМП (перемещение штока ЭМП в заданное положение 1–25 мм со скоростью не более 10 мм/сек; при этом точность позиционирования должна быть не хуже ± 0,1 мм, а потребляемый ток не должен превышать 50 А);
– точностные характеристики ЭМП (перемещение штока ЭМП в заданное положение 1–25 мм со скоростью не более 1 мм/сек; при этом точность позиционирования должна быть не хуже ± 10 мкм);
– обеспечение «форсированного» режима – заданной скорости перемещения при наложении нагрузки на выходном штоке ЭМП (перемещение штока ЭМП в заданное положение 1–25 мм со скоростью не менее 220 мм/сек при воздействии на него постоянной нагрузки в 1 кН; при этом время перемещения не должно превышать 0,1 сек).
При этом использовалось вспомогательное оборудование:
– для управления ЭМП (задания величины и скорости перемещения), а также регистрации выходных параметров (положения его рабочего органа и величины потребляемого тока) использовался технологический компьютер со специальным ПО;
– механический стенд для создания заданной нагрузки на ЭМП (~ 1 кН) при помощи пневмоцилиндра.

Рис. 5. Результат моделирования форсированного перемещения штока ЭМП на рабочий ход
Результаты исследования и их обсуждение
В результате испытаний все заданные к ЭМП требования были подтверждены снятыми характеристиками. С точки зрения обеспечения безаварийной работы турбины, наиболее важна среди них именно последняя – проверка возможности максимально быстрого перемещения ЭМП на полный рабочий ход с присоединённой (статической) нагрузкой, учитывающей как массу подвижных частей (в т.ч. и отсечного золотника (О)З, жёстко пристыкованного к ЭМП), так и трение сопрягаемых поверхностей (рис. 3).
Замеренное по ним время перемещения составило 87 мс, что удовлетворяет требованиям по скорости и точности позиционирования.
Выводы
Разработанная ранее нелинейная математическая модель ЭМП [6-8] в алгебраических и дифференциальных уравнениях с постоянными коэффициентами учитывает, помимо особенностей конструкции, также и инерционность подвижных частей самого привода, и присоединённой к нему массы отсечного золотника (рис. 4).
Первичное моделирование в ней режима форсированного перемещения штока ЭМП на рабочий ход 21 мм показывает качественную сходимость с результатами испытаний (рис. 5) на наиболее ответственном режиме. Для сравнения также приведён график «идеального» перемещения ЭМП на ход 20 мм без учёта инерционности подвижных узлов.
Указанная модель, по-видимому, может быть использована как базовая при проектировании или выборе типоразмера ЭМП под заданные условия эксплуатации, но подлежит дальнейшей проверке на прочих режимах, а также уточнению параметров её нелинейных элементов и их влияния на параметры переходного процесса.
Библиографическая ссылка
Чубаров Ф.Л., Сизов А.Н., Быков А.И. ОТРАБОТКА МОДЕЛИ ВЫСОКОТОЧНОГО БЫСТРОДЕЙСТВУЮЩЕГО СЛЕДЯЩЕГО ЭЛЕКТРОМЕХАНИЧЕСКОГО ПРИВОДА И ЕЁ ПРИМЕНЕНИЕ К СИСТЕМЕ РЕГУЛИРОВАНИЯ ПАРОВОЙ ТУРБИНЫ // Фундаментальные исследования. 2016. № 9-1. С. 91-95;URL: https://fundamental-research.ru/ru/article/view?id=40701 (дата обращения: 06.07.2025).



