Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Тувин А.А. 1 Максимов А.А. 1

---

1 ФГБОУ ВО «Ивановский государственный политехнический университет»

Разработана математическая и динамические модели задачи вынужденных колебаний батанного механизма с учетом упругой системы заправки станка, необходимой для анализа конструктивных и технологических возможностей батанного механизма при выработке сетки заданных технических характеристик. Решение задачи о вынужденных колебаниях бруса показало, что на фазе движения батана в процессе формирования сетки (взаимодействие берда с опушкой ткани) проявляются вынужденные, свободные (вызванные не­нулевыми начальными условиями) и свободные сопровождающие колебания. Полученные зависимости позволяют определить не только напряже­ния, возникающие в элементах конструкции, но и форму бруса в интересуемый момент времени, например, в момент отхода берда от опушки. При проектиро­вании цикловой диаграммы работы батана, например, с выстоем в переднем положении, возникает необходимость определения времени затухания свобод­ных и свободных сопровождающих колебаний бруса. Для этого необходимо решение задачи о собственных колебаниях бруса по начальным условиям, определяемым при решении задачи о вынужденных колебаниях на фазе движения батана в процессе формирования сетки.

Статья в формате PDF

0 KB

ткацкий станок

батан

брус

форма бруса

опушка ткани

модель

частота колебаний

1. Вульфсон И.И. Колебания машин с механизмами циклового действия / И.И. Вульфсон. – Л.: Машиностроение. – 1990. – 309 с.

2. Смирнов В.И. Курс высшей математики: Учебное пособие для втузов: В 6 т. Т. 1. / В.И. Смирнов. – М.: Наука. – 1965. – 480 с.

3. Суров В.А. Динамика упругих систем батанных механизмов металло­ткацких станков. / В.А. Суров, А.А. Тувин. – Иваново: ИГТА. – 2004. – 188 с.

4. Тувин А.А. Расчет собственных частот и форм изгибных и крутильных колебаний бруса батана широких металлоткацких станков / А.А. Тувин, А.А. Максимов // Фундаментальные исследования. – 2016. – № 8–1. – C. 65–70.

5. Филиппов А.П. Колебания деформируемых систем / А.П. Филиппов. – М.: Машиностроение. – 1970. – 736 с.

Постановка и решение динамической задачи требует соответствующего представления модели батанного механизма. Обратимся к схеме (рисунок). Брус 1 батана жестко закреплен в n лопастях 2, неподвижно соединенных с подбатанным валом 3. Вал 3 расположен в подшипниковых опорах (подшипники качения). Батан получает возвратно-качательное движение от кулачкового привода посредством коромысла 4 и шатуна 5. Соединения вал коромысла – станина, коромысло-шатун и шатун-лопасть выполнены также на подшипниках качения, обладающих радиальной податливостью.

В простейшем случае (техническая теория) уравнение вынужденных колебаний бруса во время движения батана в процессе формирования сетки имеет вид

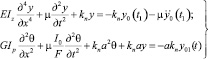, (1)

где 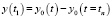– перемещение (кинематическое) бруса на рассматриваемой фазе движения батана (в дальнейшем индекс 1 будем опускать, предполагая начало отсчета времени t c момента подхода берда к опушке сетки).

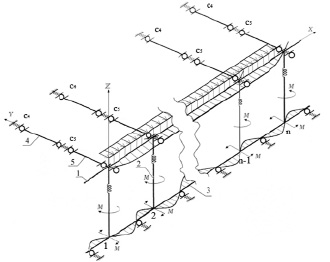
Схема упругих связей батанного механизма металлоткацкого станка типа СТР

Решение уравнения (1) ищется в виде суммы

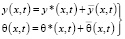, (2)

где 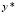– решение однородного уравнения;

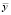– частное решение, соответствующее виду правой части.

Решение 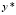, согласно [5], можно представить в виде

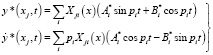, (3)

где 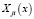– собственные формы; j – номер участка бруса (1…п-1); pi – собственные частоты изгибаемых колебаний бруса в рассматриваемой фазе его движения; 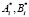– постоянные.

На основании (3) можно записать (номер участка бруса опускаем):

,

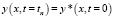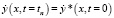, (4)

или

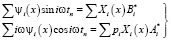. (5)

Учитывая свойство ортогональности нормальных форм колебаний из (5.20) найдем

,

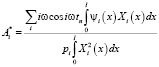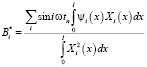, (6)

то есть решение (3) определено. Решение 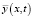ищется также в виде разложения в ряд по собственным формам:

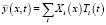
и

,

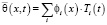где Ti(t) – искомые функции времени.

Учитывая, что

,

,

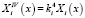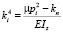получим

.

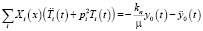При учете сил неупругого сопротивления уравнение вынужденных колебаний бруса примет вид

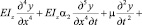
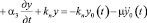. (7)

Уравнение решается аналогично предыдущему. Решение 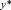принимается в виде

,

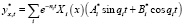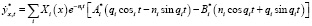, (8)

где

, .

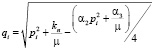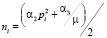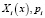– формы и частоты собственных колебаний системы без сопротивлений, рассчитываемые в соответствии с методикой, изложенной в [4]. Частное решение 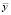ищется в той же форме (2). Подставляя (2) в уравнение (7) и учитывая, что

, ,

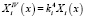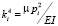получим

,

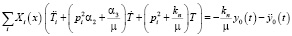следовательно,

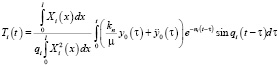. (9)

Обозначив

,

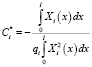будем иметь

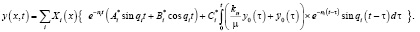
Общее решение ищется в виде суммы (2), решение 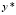однородного уравнения – в виде

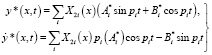. (10)

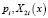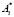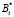Здесь – собственные частоты и формы, а коэффициенты и определяются из начальных условий. Тогда имеем

, .

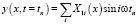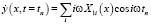Из (10), учитывая (4), получим

, .

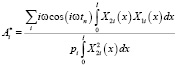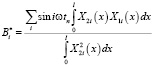Для отыскания частного решения 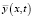, возмущающую функцию разложим в гармонический ряд

,

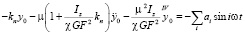где

.

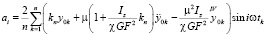Решение 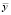ищется в виде 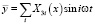. Подставляя эти выражения в исходное уравнение, будем иметь

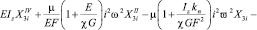
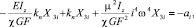
или

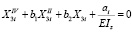, (11)

где

; .

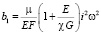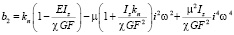Введем новую переменную 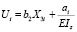. Тогда уравнение (5.39) можно представить в виде

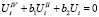. (12)

Полагая 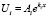, получим характеристическое уравнение

,

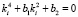откуда

,

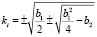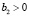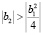так как в данном случае и , то , , , ,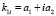

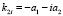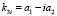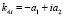где

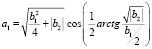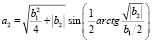, . (13)

Тогда

,

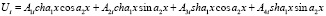и будем иметь

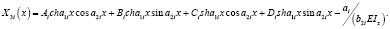(14)

Постоянные коэффициенты Ai, Bi, Ci, Di определяются из граничных условий. Подставляя (14) в граничные условия, придем к системе линейных алгебраических уравнений вида

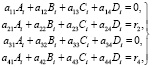. (15)

Тогда

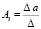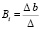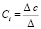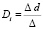; ; ; , (16)

где Δ, Δa, Δb, Δc, Δd – соответствующие определители системы (5.44).

Исключая угол β сдвига, получим

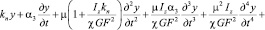
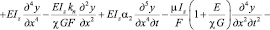
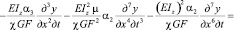
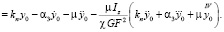(17)

Пренебрегая двумя последними членами в левой части данного уравнения, будем искать его решение в форме (2). Решение 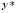однородного уравнения можно представить в виде разложения в ряд по собственным формам:

,

.

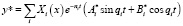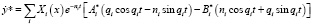где Xi(x) – собственные формы колебаний бруса на второй фазе движения батана.

Величины qi и ni определены в работе [4]. Для определения коэффициентов 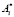и 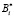воспользуемся начальными условиями. Будем иметь

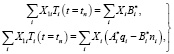откуда получаем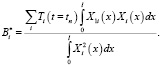

,

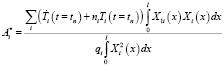где 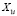– собственные формы колебаний бруса на первой фазе движения батана;

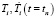– постоянные, определяемые по методике, изложенной в работе [3].

Далее остановимся на учете только первой гармоники. В предлагаемой постановке это основное допущение при приближенном решении задачи, позволяющее существенно упростить математическую модель. Принимая такое допущение, мы имеем в виду, что амплитуды колебаний системы с неупругим сопротивлением на низшей частоте являются наиболее значимыми. Кроме того, вследствие симметричности конструкции, следовательно, и ее динамической модели, четные формы колебаний не реализуются, поскольку эти формы являются кососимметричными и входящий в выражение интеграл 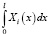для этих форм будет равен нулю. Умножив уравнение (17) на Xi(x) и проинтегрировав результат по всей длине бруса, с учетом принятого допущения это уравнение можно представить в виде

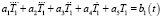, (18)

где ai – постоянные коэффициенты, определяемые по методике, изложенной в работе [3].

Для решения уравнения (18) рассмотрим однородное уравнение

,

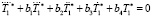где .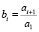

Представляя решение данного уравнения в виде 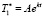, получим характеристическое уравнение 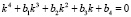. Решение этого уравнения можно получить либо по методу Феррари, либо по методу Н.И. Лобачевского [2]. Окончательный вид функции 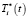будет зависеть от вида четырех корней ki характеристического уравнения [2, 5]. После нахождения функции 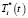решение уравнения (18) ищется методом вариации произвольных постоянных [2], при этом

,

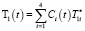где 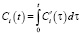, а функции 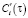находятся по формуле Крамера [2] из следующей системы уравнений:

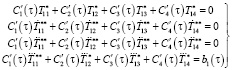. (19)

Уравнение вынужденных чисто крутильных колебаний бруса имеет вид

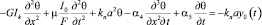. (20)

Имея в виду, что начальные условия в данном случае нулевые, поскольку в принятой постановке задачи крутильные колебания до данной фазы движения батана не возникают, решение уравнения (20) можно представить в виде

,

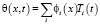где 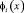– собственные формы, определяемые по методике [4]. Для определения функции Ti(t) аналогично предыдущему представим возмущающую функцию в виде разложения в ряд по собственным формам:

,

.

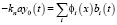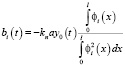Подставляя найденные выражения в исходное уравнение (20) и учитывая свойство ортогональности нормальных форм, а также то, что 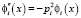, получим

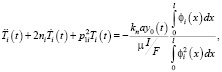
где 2ni и 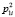определяются по методике, изложенной в [3]. Следовательно,

, ,

.

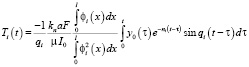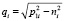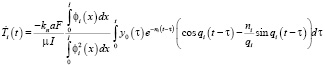Полученные выше зависимости позволяют определить не только напряжения, возникающие в элементах конструкции, но и форму бруса в интересуемый момент времени, например, в момент отхода берда от опушки. При проектировании цикловой диаграммы работы батана, например, с выстоем в переднем положении, возникает необходимость определения времени затухания свободных и свободных сопровождающих колебаний бруса. Для этого необходимо решение задачи о собственных колебаниях бруса по начальным условиям, определяемым при решении задачи о вынужденных колебаниях на второй фазе движения батана.

Выводы

Разработана математическая модель расчета вынужденных колебаний бруса батана широких металлоткацких станков с n лопастями, соответствующая его уточненной динамической модели на фазе взаимодействия берда с опушкой вырабатываемой сетки.

Библиографическая ссылка