В работе [3] построена физико-математическая модель движения мелких монодисперсных твердых частиц в потоке ньютоновской жидкости в вертикальных трубах, основанная на представлении, что линейный масштаб турбулентности λt существенно больше диаметра частиц d, то есть λt >> d [1]. В данной работе рассматривается другой предельный случай, а именно, принимается, что размер частиц порядка или более линейного масштаба турбулентности, то есть λt ≤ d [1]. Величину максимального линейного масштаба λt определим выражением, приведенным в [1]:
λt = 0,03R, (1)
где R – характерный размер потока в поперечном направлении – радиус трубы.
В работе [1] отмечается, что в этом случае крупные частицы «движутся по траекториям, на которые не влияет мелкая турбулентная структура окружающей жидкости». На основании этого представления, при анализе смеси жидкости с крупными твердыми частицами, исключим из рассмотрения силу турбофореза Ftf, поскольку причиной возникновения силы турбофореза является наличие мелкомасштабных турбулентных пульсаций потока.
Силы Fp, FA, Fg и Fr определяются следующими выражениями:
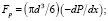
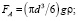
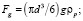
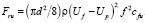 , (2)
, (2)
где d – диаметр частицы; 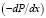 – составляющая градиента давления, действующая на твердую частицу в направлении движения, в рассматриваемом случае вверх; r и rp – плотность жидкости и материала твердых частиц, соответственно; g – ускорение силы тяжести; Uf и Up – скорости движения жидкости и частиц в направлении движения потока вверх; f – коэффициент стесненности, учитывающий стесненное движение жидкости в межчастичном пространстве; cfu – коэффициент гидравлического сопротивления сферической частицы; коэффициента стесненности f определяется выражением [3]:
– составляющая градиента давления, действующая на твердую частицу в направлении движения, в рассматриваемом случае вверх; r и rp – плотность жидкости и материала твердых частиц, соответственно; g – ускорение силы тяжести; Uf и Up – скорости движения жидкости и частиц в направлении движения потока вверх; f – коэффициент стесненности, учитывающий стесненное движение жидкости в межчастичном пространстве; cfu – коэффициент гидравлического сопротивления сферической частицы; коэффициента стесненности f определяется выражением [3]:
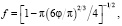
где j – объемная доля частиц твердой фазы; cfu – коэффициент гидравлического сопротивления сферической частицы.
Считая процесс движения установившимся в соответствии с методом Лагранжа уравнение, определяющее скорость движения частицы относительно жидкости, записывается в виде баланса сил, действующих на твердую частицу:
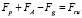 . (3)
. (3)
Коэффициент гидравлического сопротивления cfu определяется по формуле Озеена:
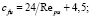 (4)
(4)
где 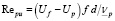 – число Рейнольдса, определенное по фактической скорости стесненного движения жидкости в межчастичном пространстве
– число Рейнольдса, определенное по фактической скорости стесненного движения жидкости в межчастичном пространстве 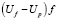 , диаметру частицы d и кинематической вязкости двухфазного потока, определяемой по формуле
, диаметру частицы d и кинематической вязкости двухфазного потока, определяемой по формуле
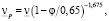
где 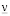 – кинематическая вязкость несущей жидкости; числа 0,65 и 1,675 – эмпирические коэффициенты [4].
– кинематическая вязкость несущей жидкости; числа 0,65 и 1,675 – эмпирические коэффициенты [4].
Подставляя приведенные выражения в (3), получим
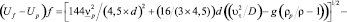
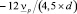 (5)
(5)
где 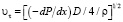 – динамическая скорость, D – диаметр трубопровода.
– динамическая скорость, D – диаметр трубопровода.
Если число Рейнольдса значительно отличается от 4,5, то в выражении (5), вместо постоянного коэффициента 4,5 следует использовать величину 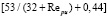 , и расчет по формуле (5) ведется путем итераций.
, и расчет по формуле (5) ведется путем итераций.
В работе [3] показано, что если использовать гипотезу Прандтля о распределении турбулентного трения с введением поправки на присутствие в потоке твердых частиц, то выражение для профиля скорости записывается в виде
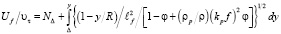 . (6)
. (6)
где NΔ – относительная скорость двухфазной среды на расстоянии толщины приповерхностной зоны течения; Δ – толщина приповерхностной зоны движения двухфазной среды; y – расстояние от поверхности нижней образующей трубы;
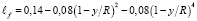 –
–
длина пути смешения жидкости; y – расстояние от поверхности трубы; kpj – коэффициент, определяемый отношением усредненного квадрата пульсационной скорости частицы к усредненному квадрату пульсационной скорости жидкости [3] при характерной частоте, определяющей теоретическое значение нестационарной скорости осаждения частиц под действием силы тяжести [1].
Величина NΔ определяется зависимостью [5]
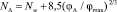 , (7)
, (7)
где 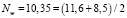 – среднее значение для поверхности трубы действительная степень шероховатости, которой неизвестна; φΔ – объемная доля частиц на расстоянии Δ от стенки трубы; φmax – максимальная объемная доля твердых частиц, соответствующая предельно шероховатой поверхности. Например, если сферические частицы и расположены в виде простой кубической решетки, то
– среднее значение для поверхности трубы действительная степень шероховатости, которой неизвестна; φΔ – объемная доля частиц на расстоянии Δ от стенки трубы; φmax – максимальная объемная доля твердых частиц, соответствующая предельно шероховатой поверхности. Например, если сферические частицы и расположены в виде простой кубической решетки, то 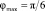 . Если же частицы имеют форму откалиброванных песчинок, например, кубической формы, то φmax = 1. В формуле (7) второй член в правой части учитывает проскальзывание (скачок скорости) на «поверхности шероховатого квазитвердого тела», образованного движущимся придонным слоем твердых частиц ближайшего к поверхности, со стороны, обращенной к поверхности трубы [5].
. Если же частицы имеют форму откалиброванных песчинок, например, кубической формы, то φmax = 1. В формуле (7) второй член в правой части учитывает проскальзывание (скачок скорости) на «поверхности шероховатого квазитвердого тела», образованного движущимся придонным слоем твердых частиц ближайшего к поверхности, со стороны, обращенной к поверхности трубы [5].
Величина Δ определяется как сумма толщин подслоев жидкости на поверхности стенки трубы и диаметра частиц d: 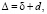 где
где 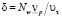 .
.
В работе [3] показано, что при установившемся осесимметричном движении взвесенесущего потока, распределение объемной концентрации твердой фазы в поперечном направлении определяется выражением
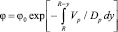 , (8)
, (8)
где j0 – объемная концентрация твердой фазы на оси трубы; Vp – скорость перемещения частиц в горизонтальном направлении; Dp – коэффициент диффузии твердых частиц в жидкости.
Средняя по поперечному сечению трубы объемная доля частиц твердой фазы определяется выражением
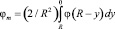 ; (9)
; (9)
где jm – средняя объемная концентрация частиц твердой фазы.
Выражение коэффициента турбулентной диффузии для частиц Dp можно представить в виде зависимости [2]
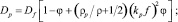 (10)
(10)
где коэффициент диффузии жидкости Df определяется эмпирическим выражением
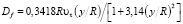 . (11)
. (11)
В поперечном, горизонтальном направлении на движущиеся частицы действует сила Магнуса:
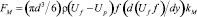 , (12)
, (12)
где 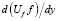 – градиент скорости жидкости при стесненном обтекании твердых частиц; у – расстояние от поверхности; kM – поправочная функция для силы Магнуса.
– градиент скорости жидкости при стесненном обтекании твердых частиц; у – расстояние от поверхности; kM – поправочная функция для силы Магнуса.
Сила Сафмана также действует в горизонтально направлении:
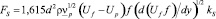 ; (13)
; (13)
где kS – поправочная функция для силы Сафмана.
На основе проведенного анализа рекомендуется использовать следующие поправочные зависимости.
Для величины kM для диапазона 0,5 < Rep < 140×103; 0,1 < Γ < 7 [6];
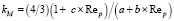 , (14)
, (14)
где a = 1,333 – 0,061×Г + 0,029×Г2, b = (5,9 + Г)/(39 + 4,6×Г), с = 1/(25 + 21×Г).
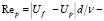 поступательное число Рейнольдса частицы;
поступательное число Рейнольдса частицы; 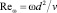 – вращательное число Рейнольдса; ω – угловая скорость вращения частицы относительно окружающей среды; в случае если жидкость в поперечном сечении потока не вращается, то принимается, что
– вращательное число Рейнольдса; ω – угловая скорость вращения частицы относительно окружающей среды; в случае если жидкость в поперечном сечении потока не вращается, то принимается, что 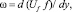 а
а 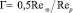 – число вращения.
– число вращения.
Для величины FS, при использовании в качестве параметра, определяющего диапазон использования рекомендуемых зависимостей, величины 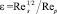 , где
, где 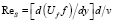 – число Рейнольдса частицы, определенное по скорости сдвига жидкости, используются следующие зависимости [9]:
– число Рейнольдса частицы, определенное по скорости сдвига жидкости, используются следующие зависимости [9]:
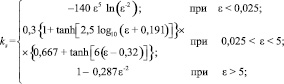 (15)
(15)
Из последней зависимости следует, что величина kS знакопеременна, а значит, направление действия силы Сафмана может изменяться на противоположное направление.
Сила гидродинамического сопротивления в горизонтальном направлении, подобно выражению, приведенному в (2), определяется выражением
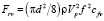 , (16)
, (16)
где Vp – скорость движения частицы в горизонтальном направлении; cfv – коэффициент гидравлического сопротивления, определяемый по скорости Vpf; рассчитывается по формуле (4) с соответствующей заменой величины Рейнольдса Repu на 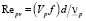 .
.
Скорость движения твердых частиц в поперечном направлении Vp определим из условия, что в поперечном направлении к оси потока на частицы действуют силы Магнуса FM и Сафмана FS противоположно направленной, силой гидродинамического трения Frv:
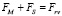 . (17)
. (17)
Отметим, что при записи правой части выражения (17) учитывалось, что в установившемся режиме при движении частиц от стенки трубы в направлении к оси, навстречу ему перемещается такой поток частиц за счет диффузии, вследствие чего результирующая скорость жидкости в поперечном направлении равна нулю, то есть принимается, что частицы перемещаются в неподвижной жидкости. Подставляя выражения (12)÷(16), с учетом (4), в (17) и разрешая его относительно Vp, получим
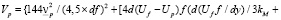
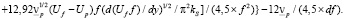 (18)
(18)
Если второй член в аналоге формулы (4) существенно отличается от 4,5, то также используется рассмотренный выше итерационный процесс вычислений.
При известном распределении скорости жидкости, рассчитанном по формуле (6), рассчитываются распределения скоростей твердых частиц по формуле
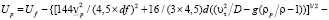
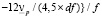 . (19)
. (19)
Объемный расход жидкой и твердой фаз рассчитывается по формулам:
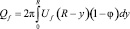 , (20)
, (20)
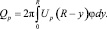 (21)
(21)
Суммарный объемный расход взвесенесущего потока равен 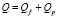 .
.
Средняя объемная скорость равна
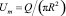 . (22)
. (22)
При движении в вертикальных каналах общий перепад давления должен включать изменение потенциальной энергии при перемещении двухфазного потока, поэтому общий перепад давления равен
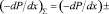
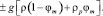 (23)
(23)
В выражении (23) знак + относится к случаю движения двухфазного потока снизу вверх, а знак – к движению в обратном направлении.
При заданных градиенте давления и средней объемной доли твердых частиц и их размере приведенные соотношения позволяют рассчитать все локальные характеристики взвесенесущего потока монодисперсных твердых частиц, включая профили скорости жидкости и твердых частиц и поперечное распределение объемной доли частиц, и интегральные величины двухфазного потока: среднюю скорость и суммарную объемную долю твердых частиц. Порядок вычислений следующий. Задается произвольное значение концентрации твердой фазы, например, на оси потока, j0. Далее итеративным путем определяются все характеристики двухфазного потока на некотором малом расстоянии dy. После нахождения локальных значений скоростей и объемных долей частиц, определяются интегральные показатели двухфазного потока Um и jm. При необходимости расчет повторяется при новом значении j0. Расчет завершается при малом (допустимом) отличии значений jm от заданного значения.
В случае если движение взвесенесущего потока направлено вниз, то силы, определяемые градиентом давления в жидкости Fp и тяжести Fg, направлены вниз, а сила Архимеда FA – вверх, и этом случае частицы опережают жидкость, в соответствии с чем преобразуются приведенные выше выражения.
Изложенный метод расчета позволяет определить полный набор характеристик монодисперсного взвесенесущего потока без привлечения каких-либо коррелирующих эмпирических зависимостей, определяемых из сопоставления опытных и расчетных данных по гидродинамике двухфазного потока.
В рамках сформулированной проблемы проанализируем экспериментальные данные работы [10], в которой приведены опытные данные по движению смеси воды с частицами песка размером 470 мкм и 1700 мкм в трубопроводе с внутренним диаметром 0,040 м. В опытах измерялось распределение объемной доли частиц j и их скорости Up в радиальном направлении при различных средних объемных долях твердой фазы и при различных скоростях движения смеси. Величина максимального линейного масштаба турбулентности. λt, определенная по формуле (1), равна λt = 0,03×0,020 = 600 мкм. Поскольку в обоих случаях частицы имеют линейный размер, близкий или превосходящий максимальный линейный масштаб турбулентности λt, может быть использован рассмотренный метод расчета. В данных расчетах также принималось, что отсутствует механическое трение твердых частиц о поверхность стенки трубы.
В таблице приведены основные интегральные характеристики экспериментов и соответствующие расчетные величины, которые определялись по изложенной методике. Плотность материала частиц rp = 2650 кг/м3, жидкости ρ = 1000 кг/м3, кинематическая вязкость жидкости n = 10-6 м2/с.
Сопоставление приведенных опытных данных с расчетными профилями распределения объемной доли твердой фазы и скоростей частиц ранее выполнялось в работах [7, 8]. Используемый метод расчета основывался на использовании различных физических моделях турбулентности основанных на кинетической теории гранулированных потоков с использованием коммерческого программного продукта ANSYS CFX-4-4.
Основные интегральные характеристики экспериментов и соответствующие расчетные величины
|
№ п/п |
d, мкм |
Опыт |
Расчет |
|||
|
φm |
Um, м/с |
φm |
Um,м/с |
Umах, м/с |
||
|
1 |
470 |
0,087 |
2,6 |
0,0867 |
2,65 |
3,09 |
|
2 |
470 |
0,278 |
2,6 |
0,277 |
2,65 |
3,03 |
|
3 |
1700 |
0,085 |
2,8 |
0,0849 |
2,85 |
3,45 |
|
4 |
1700 |
0,177 |
2,8 |
0,176 |
2,77 |
3,28 |
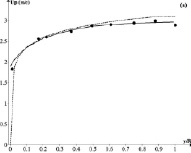
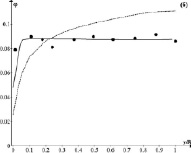
Рис. 1. Сравнение измеренных и результатов расчетов для частиц с d = 470 мкм и средней объемной долей частиц jm = 0,087: (a) скорости твердых частиц и (б) объемной доли частиц. Точки – опыт [10]; сплошная кривая – расчет [8]; пунктирная кривая – наш расчет
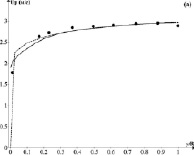
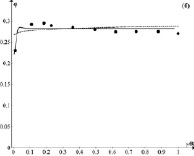
Рис. 2. Сравнение измеренных и результатов расчетов для частиц с d = 470 мкм и средней объемной долей частиц jm = 0,278: (a) скорости твердых частиц и (б) объемной доли частиц. Точки – опыт [10]; сплошная кривая – расчет [8]; пунктирная кривая – наш расчет
На рис. 1 приведено распределение объемной доли твердой фазы и скорости частиц для условий первого опыта.
Сравнение опытных данных по профилю скорости частиц Up показывает, что расчет по рассмотренной методике и методу работ [7, 8] достаточно хорошо совпадают. В обоих случаях расчетные распределения объемной доли твердой фазы j отличаются от экспериментальных данных в значительно большей мере. Опытные данные по всему поперечному сечению трубы близки к постоянному значению примерно равному среднему значению, φm = 0,087. Ни один из методов не отражает локальное уменьшение величины φ при значении y/R = 0,23. Метод расчета работ [7, 8] лучше согласуется с опытными данными, хотя и различие между изложенным методом и опытными значениями φ в области 0,2 ≤ y/R ≤ 1 не превосходит 15 %.
На рис. 2 приведено распределение объемной доли твердой фазы и скорости частиц для условий второго опыта.
Так же, как в предыдущем случае, сравнение опытных данных по профилю скорости частиц Up показывает, что расчет по рассмотренной методике и методу работ [7, 8] достаточно хорошо совпадает. Также имеется достаточно удовлетворительное соответствие между обоими расчетными методами и опытными значениями j. Ни один из методов не отражает локальное увеличение величины φ при значении y/R = 0,1.
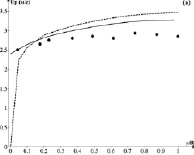
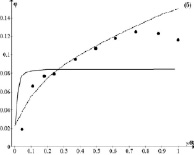
Рис. 3. Сравнение измеренных и результатов расчетов для частиц с d = 1700 мкм и jm = 0,085: (a) скорости твердых частиц и (б) объемной доли частиц. Точки – опыт [10]; сплошная кривая – расчет [8]; пунктирная кривая – наш расчет
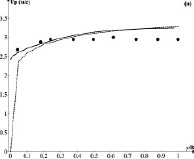
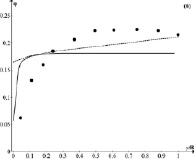
Рис. 4. Сравнение измеренных и результатов расчетов для частиц с d = 1700 мкм и средней объемной долей частиц jm = 0,177: (a) скорости твердых частиц и (б) объемной доли частиц. точки – опыт [10]; сплошная кривая – расчет [8]; пунктирная кривая – наш расчет
На рис. 3 приведено распределение объемной доли твердой фазы и скорости частиц для условий третьего опыта.
Сравнение опытных данных по профилю скорости частиц Up показывает, что расчет по рассмотренной методике и метод работ [7, 8] несколько лучше совпадает с опытными данными, хотя и расчет по рассмотренной методике достаточно хорошо совпадает с опытными данными. Сравнение опытных данных по распределению объемной доли твердой фазы j показало, что расчетные зависимости по методике работ [9, 10] в области 0,3 ≤ y/R ≤ 1 с погрешностью около 50 % отличаются от опытных данных. Качественный характер расчетной зависимости практически полностью повторяет аналогичные зависимости на рис. 1, а и 2, а. В этой области потока различия между опытными и расчетными значениями j по изложенной методике существенно меньше, хотя в области 0,9 ≤ y/R ≤ 1 также весьма значительно. Ни один из методов не отражает локальное увеличение величины j при значении y/R = 0,75.
На рис. 4 приведено распределение объемной доли твердой фазы и скорости частиц для условий второго опыта.
Также как в предыдущем случае сравнение опытных данных по профилю скорости частиц Up показывает, что расчет по рассмотренной методике и методы работ [7, 8] несколько лучше совпадают с опытными данными, хотя и расчет по рассмотренной методике достаточно хорошо совпадает с опытными данными.
Качественный характер расчетной зависимости j по методике работ [7, 8] практически полностью повторяет аналогичные зависимости на рис. 1, а, 2, а и 3, а и достаточно значительно отличается от опытных данных. Расчет по рассмотренной методике значительно лучше согласуется с опытными данными во всем диапазоне 0,05 ≤ y/R ≤ 0,1. Следует отметить, что и в этом случае ни один из методов не отражает локальное увеличение величины j при значении 0,6 ≤ y/R ≤ 0,75.
Проведенный сравнительный анализ показал, что рассмотренная методика дает лучшее соответствие с опытными данными с более крупными частицами, когда отношение величин (d/λt) = (1700/600) = 2,83 существенно больше единицы, хотя и для частиц меньшего диаметра (d/λt) = (470/600) = 0,783 результаты сравнения опытных и расчетных данных достаточно удовлетворительны. В работе [8] в связи с большим отличием опытных и расчетных данных по j, для частиц большого размера, отмечается, что развитая авторами модель расчета не в состоянии учесть особенности движения частиц большого размера. Эта констатация, как нам представляется, свидетельствует о том, что использование достаточно сложных моделей турбулентности двухфазного потока не обеспечивает необходимой общности, а, как и любая другая более простая модель турбулентности двухфазного потока, требует «настройки» на процессы, которые являются определяющими в том или ином конкретном случае.
Библиографическая ссылка
Кондратьев А.С., Ньа Т.Л. ОСНОВЫ РАСЧЕТА ГИДРОДИНАМИЧЕСКИХ ПАРАМЕТРОВ ПРИ ДВИЖЕНИИ ЖИДКОСТИ С МОНОДИСПЕРСНЫМИ КРУПНЫМИ ТВЕРДЫМИ ЧАСТИЦАМИ В ВЕРТИКАЛЬНЫХ ТРУБАХ // Фундаментальные исследования. 2016. № 9-1. С. 35-42;URL: https://fundamental-research.ru/ru/article/view?id=40691 (дата обращения: 21.12.2025).



