Связи и зависимости – понятия, широко применяемые в различных сферах экономики. Различают два их вида: функциональные и корреляционно-регрессивные. Первые представляют собой точные и однозначные связи (зависимости), вторые – выражают усредненные или приближенные связи (зависимости) для совокупности объектов, называемой статистической (выборочной) совокупностью. Связи и зависимости принято выражать в виде математических формул (равенств, неравенств, уравнений). Если зависимость одного экономического показателя от одного, двух и более других выражена в виде уравнения, то зависимый показатель принято называть результативным, а независимые – показателями-факторами. Среди связей и зависимостей в экономике особое место занимают таковые между показателями затрат ресурсов и выпуска продукции, которые называются производственными функциями [1, 2, 3, 4, 5].
К показателям, на основе которых можно строить модели производственных функций на региональном уровне, можно отнести в первую очередь четыре ключевых показателя: валовой региональный продукт, стоимость основных фондов, численность занятых в экономике и инвестиции. Данные по этим показателям публикуются в статистических ежегодниках «Россия в цифрах». Экономики регионов существенно различаются. Поэтому целесообразно проводить анализ моделей производственных функций не только в целом по стране, но и в разрезе различных групп регионов. Модели производственных функций групп регионов и страны в целом различаются и за разные временные периоды. Иными словами, актуальность исследований, посвященных выявлению, описанию и анализу производственных функций экономических объектов любого уровня, не вызывает сомнений.
Группировать регионы, как и другие экономические объекты, можно по-разному. В частности, все регионы нами разбиты на три группы: малые, средние и крупные. Деление регионов на группы осуществлено по показателю «валовой региональный продукт». Для рассматриваемых показателей приняты следующие обозначения: для валового регионального продукта – Y, в млрд руб.; стоимости основных фондов – K, млрд руб., численности занятых в экономике – L, в тыс. чел., объемов инвестиций – I, в млрд руб. При этом построены и анализируются две двухфакторные зависимости:
а) валового регионального продукта от стоимости основных фондов и численности занятых в экономике (Y от K, L);
б) валового регионального продукта от численности занятых в экономике и объемов инвестиций (Y от L, I).
Для каждой группы регионов и в целом по всем регионам за каждый год построены по четыре уравнения (два линейных и два степенного вида) производственных функций:
– линейного вида
Y = b + m1·K + m2·L; Y = b + m1·L + m2·I;
– степенного вида
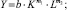
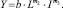
Расчет и анализ статистических характеристик для других видов уравнений (гиперболического, показательного и полиномиального и др.) показал, что их приемлемость для оценки искомых зависимостей существенно ниже, чем уравнений линейного и степенного видов. Выполнены следующие расчеты: параметров, статистических характеристик и ряда производных показателей (табл. 1).
Перечисленные показатели из табл. 1 можно рассчитать с помощью разных методов и моделей. Все расчеты нами выполнены с помощью встроенных математических и статистических функций из MS Excel. Величины рассчитанных показателей уравнений для двухфакторных производственных функций линейного вида, выражающих зависимость ВРП от затрат ресурсов для всей совокупности регионов страны, характеризуют данные, приведенные в табл. 2. Такие же показатели рассчитаны и для трех групп регионов.
Параметр b (свободный член уравнения) в уравнениях регрессии линейного вида не имеет экономического смысла, но параметры при независимых показателях-факторах (m1, m2 и m2, m3) всегда имеют экономический смысл: они показывают величину роста результативного показателя Y (ВРП, в млрд руб.) при увеличении каждого из ресурсов на одну абсолютную единицу.
Отметим также, что одна из важных статистических характеристик, называемая предельной эффективностью и определяемая как производная Y по K (Y по L; Y по I), численно равна коэффициенту при показателе-факторе, т.е.
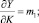
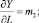
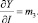
Таблица 1
Перечень рассчитываемых показателей и их обозначение
|
Параметры (1, 2, 3, 4): b – свободный член m1, m2, m3 – коэффициенты регрессии при переменных K, L, I |
|
Статистические характеристики (5, 6, … ,15): seb, se1, se2, se3 – стандартные ошибка для параметров b, m1, m2, m3 sey – стандартная ошибки для Y R – индекс детерминации df – число степеней свободы F – критерий Фишера SSreg, SSresid – регрессионная и остаточная суммы квадратов A – средняя ошибка аппроксимации |
Таблица 2
Величины параметров и статистических характеристик, рассчитанные и анализируемые для линейных двухфакторных моделей производственных функций по данным для всей совокупности регионов России, построенных по данным за 2005, 2010 и 2014 гг.
|
2005 |
2010 |
2014 |
|||||
|
Y от K, L |
Y от L, I |
Y от K, L |
Y от L, I |
Y от K, L |
Y от L, I |
||
|
1 |
b |
–15,1 |
–6,2 |
–42,8 |
–41,9 |
–87,8 |
–63,4 |
|
2 |
m1 |
0,3413 |
0,2969 |
0,2965 |
|||
|
3 |
m2 |
0,0326 |
0,1005 |
0,1456 |
0,2888 |
0,2952 |
0,3953 |
|
4 |
m3 |
1,765 |
1,2251 |
1,8223 |
|||
|
5 |
seb |
5,8 |
5,7 |
14,0 |
16,3 |
21,8 |
25,8 |
|
6 |
se1 |
0,0391 |
0,0343 |
0,0315 |
|||
|
7 |
se2 |
0,0189 |
0,0111 |
0,0372 |
0,0305 |
0,0541 |
0,0594 |
|
8 |
se3 |
0,1889 |
0,2033 |
0,2675 |
|||
|
9 |
sey |
31,1 |
30,0 |
76,1 |
88,3 |
120,2 |
139,5 |
|
10 |
R |
0,9334 |
0,938 |
0,9313 |
0,9074 |
0,9431 |
0,9233 |
|
11 |
df |
74 |
74 |
75 |
75 |
75 |
75 |
|
12 |
F |
518,4 |
560,2 |
508,1 |
367,4 |
621,1 |
451,3 |
|
13 |
SSreg |
71712 |
66698 |
434003 |
584810 |
1082992 |
1459218 |
|
14 |
SSresid |
1004798 |
1009811 |
5880781 |
5729973 |
17938500 |
17562273 |
|
15 |
A |
24,2 |
23,4 |
26,9 |
31,3 |
25,1 |
29,1 |
По величинам параметров m1, m2 и m2, m3 построенных нами уравнений производственных функций, характеризующим предельную эффективность использования основных фондов, трудовых ресурсов и инвестиций, можно сформулировать следующие выводы:
– по данным за 2005 г. параметр m1 по группам регионов от малых до крупных увеличивался, т.е. предельная эффективность основных фондов росла; предельная эффективность трудовых ресурсов в малых регионах оказалась положительной, а в средних и крупных – отрицательной; в 2010 и в 2014 годах предельная эффективность основных фондов и трудовых ресурсов была положительной и росла вместе с увеличением размеров регионов (исключение составила эффективность основных фондов в 2010 г. – по малым регионам она оказалась выше, чем по средним);
– величина предельной эффективности основных фондов (m1) по группам регионов в динамике изменялась следующим образом: по малым в 2010 г. увеличилась, в 2014 г. уменьшилась; по средним – наоборот; по крупным регионам в оба периода увеличилась; в среднем по всем регионам предельная эффективность в динамике уменьшилась; предельная эффективность трудовых ресурсов в динамике выросла по всем трем группам регионов и по всем регионам в целом;
– в соответствии с параметрами зависимости Y от L, I: эффективность трудовых ресурсов (m2) в 2005 г. по группам регионов от малых до крупных снизилась, в 2014 г. имело место уменьшение – рост; эффективность инвестиций (m3) менялась по схеме уменьшение – рост в 2005 г., рост-уменьшение в 2010 и рост в 2014 г.; динамика изменения m2 по рассматриваемым периодам была следующей: по малым, средним и по всем регионам имел место рост, по крупным – рост – уменьшение; динамика изменения m3: по малым регионам – уменьшение, по средним – рост, по крупным и по всем регионам – уменьшение – рост.
Построенные уравнения производственных функций целесообразно записывать в математическом виде. В качестве примера в табл. 3 приведена математическая запись линейных уравнений для производственных функций за 2014 г.
Из табл. 3 видно, что:
– во-первых, предельные эффективности обоих ресурсов (т.е. параметры m1 и m2) для зависимости Y от K, L в 2014 г. и параметра m3 в уравнениях производственных функций для зависимости Y от L, I по группе средних регионов выше, чем по малым, но ниже, чем по группе крупных;
– во-вторых, величина параметра m2 в уравнениях для производственных функций, выражающих зависимость Y от L, I являются максимальной по группе малых регионов, а минимальной – по группе средних регионов;
Таблица 3
Математическая запись уравнений производных функций линейного вида, построенных по данным регионов России за 2014 г.
|
Группы регионов |
Математическая запись уравнений производственных функций |
|
|
Для зависимости Y от K, L |
m1 + m2 |
|
|
Малые |
Y = 19,8 + 0,1572·K + 0,1849·L |
0,3421 |
|
Средние |
Y = 39,4 + 0,1864·K + 0,1943·L |
0,3807 |
|
Крупные |
Y = –129,4 + 0,2614·K + 0,3891·L |
0,6505 |
|
Все регионы |
Y = –87,8 + 0,2965·K + 0,2952·L |
0,5917 |
|
Для зависимости Y от L, I |
m2 + m3 |
|
|
Малые |
Y = 16,1 + 0,2762·L + 0,8682·I |
1,1444 |
|
Средние |
Y = 106,8 + 0,1590·L + 1,3238·I |
1,4828 |
|
Крупные |
Y = –78,8 + 0,2727·L + 2,6038·I |
2,8765 |
|
Все регионы |
Y = –63,4 + 0,3953·L + 1,8223·I |
2,2176 |
– в-третьих, суммарные величины m1 + m2 и m2 + m3 в разрезе регионов растут от малых до крупных.
Отметим, что суммарные величины m1 + m2 и m2 + m3 показывают абсолютную величину роста ВРП (в млрд руб.) при одновременном увеличении каждого из ресурсов на одну абсолютную единицу:
а) стоимости основных фондов на 1 млрд руб. и численности занятых в экономике на 1 тыс. чел.;
б) численности занятых в экономике на 1 тыс. чел. и объема инвестиций на 1 млрд руб.
Преимущественно двух факторных и более уравнений регрессии по сравнению с однофакторным уравнением состоит в том, что с их помощью можно определить ряд ценных аналитических показателей, среди которых особое место занимают изокванта и предельные нормы взаимозаменяемости показателей-факторов.
Изоквантой называется совокупность значений показателей-факторов, при которых результативный показатель принимает одно и то же значение.
Изокванта представляет собой математическую формулу, с помощью которой один из показателей факторов выражен через другие. При этом величина зависимого показателя принимается за постоянную величину (const). По данным табл. 3 покажем, например, методику составления формулы для изокванты для зависимости Y от K, L:
1) Y = 19,8 + 0,1572·K + 0,1849·L;
2) Примем Y за const и выразим K через L, т.е.
K = 0,1572
и/или L = (Y – 19,8 + 0,1572·K)/0,1849 с. 6.
Приняв величину ВРП равной ее средней арифметической величине и выполнив соответствующие расчеты, авторы получили следующие уравнения изоквант для всех регионов России за три рассматриваемых временных периода:
за 2005 г. K = 4140,8 – 0,0907·L;
за 2010 г. K = 1096,7 – 0,4904·L;
за 2014 г. K = 2049,9 – 0,9956·L.
Как известно, в уравнениях производственных функций показатели-факторы (в нашем случае K и L; L и I) являются взаимозаменяемыми. В соответствии с теорией о производственных функциях можно определить предельные нормы этих взаимозаменяемостей.
Они определяются по формулам изоквант как произведение одних показателей-факторов от других. В нашем случае это есть производные: 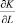 и
и 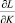 [1, 4, 5].
[1, 4, 5].
В случае производственных функций линейного вида предельные нормы взаимозаменяемости являются числовыми величинами, получаемыми по формулам m2/m1 и m1/m2. Предельная норма взаимозаменяемости показывает, какая величина одного ресурса требуется, чтобы заменить одну единицу другого. В нашем случае в соответствии с уравнениями производственных функций за 2014 г., чтобы заменить численности работников в 1 тыс. чел. требовалось основных фондов: малым регионам – 1,176; средним – 1,042; крупным – 1,489 и регионам в целом по стране – 0,996 млрд руб.
Как показывает анализ, предельные нормы основных фондов и инвестиций, требуемые для замены 1 тыс. чел., по группам регионов и в целом по стране увеличились в разы.
Проведенный нами анализ коэффициентов отношений предельных норм групп средних и крупных регионов к их величинам по группе малых регионов (малые регионы приняты за 1,00) показывает отсутствие однозначного влияния размеров регионов на величины предельных норм взаимозаменяемости ресурсов.
Главными аналитическими показателями уравнений регрессии, в т.ч. и для производственных функций являются параметры, изокванты, предельные нормы взаимозаменяемости показателей-факторов и др.
Однако, прежде чем анализировать перечисленные параметры, требуется оценить: во-первых, наличие зависимости, ее вид и степень точности этой зависимости; во-вторых, сравнительную приемлемость различных видов уравнений (как линейного, так и нелинейного видов).
Для решения таких задач эконометрической теорией предложен инструментарий статистических характеристик. Некоторые из таких характеристик приведены в табл. 1.
В учебной литературе по эконометрике рассматривают около трех десятков таких характеристик [1, 4, 5]. Для оценки приемлемости уравнений нет необходимости рассчитывать и анализировать все эти характеристики. С нашей точки зрения, можно ограничиться рассмотрением наиболее значимых характеристик, к которым можно отнести: стандартную ошибку для зависимой переменной (sey), коэффициент детерминации (R), F-критерий Фишера, среднюю ошибку аппроксимации и др. Три из этих характеристик определены средствами статистических функций MS Excel, а четвертый – средняя ошибка аппроксимации рассчитана по формуле
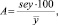
где sey – стандартная ошибка для y; 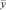 – средняя арифметическая величина ВРП.
– средняя арифметическая величина ВРП.
В табл. 4 приведены величины статистических характеристик для уравнений производственных функций линейного вида, выражающих зависимость ВРП (Y) от стоимости основных фондов (K), численности занятых в экономике (L) и объема инвестиций (I) по группам регионов России за 2005, 2010 и 2014 гг.
В соответствии с величиной R (коэффициент детерминации) из табл. 4 все уравнения производственных функций для малых, крупных и всех регионов являются приемлемыми, поскольку величина этого коэффициента составляет более 0,8 и считается высокой. Для группы средних регионов величины R ниже, чем для других групп регионов, но также являются приемлемыми (корреляционную связь можно считать средней), исключение составляет зависимость ВРП от L и I за 2005 г. (R = 0,32), но и такую связь можно считать приемлемой (на удовлетворительном уровне).
По величине F-критерия Фишера все уравнения производственных функций можно считать приемлемыми (но также в разной степени).
Более определенные выводы о приемлемости можно делать по средней ошибке аппроксимации (A). Если величина A менее 10 %, то связь считается хорошей. Таких связей в нашем случае нет. В семи случаях из 12-ти для зависимости Y от K, L 10 < А < 20, а в остальных случаях 20 < А < 22. Примерно такая же картина наблюдается и для зависимости Y от L, I: в пяти случаях А < 20, а в остальных случаях 20 < А < 26 [1, 4, 5].
Таблица 4
Величины статистических характеристик для уравнений производственных функций линейного вида, выражающих зависимость ВРП (Y) от стоимости основных фондов (K), численности занятых в экономике (L) и объема инвестиций (I) по группам регионов России за 2005, 2010 и 2014 гг.
|
Y от K, L |
Y от L, I |
||||||||
|
Ycp |
sey |
R |
F |
A |
sey |
R |
F |
A |
|
|
2005 |
|||||||||
|
Малые |
34,7 |
5,3 |
0,9273 |
153,1 |
15,3 |
5,4 |
0,9239 |
145,6 |
15,6 |
|
Средние |
97,9 |
21,2 |
0,5368 |
13,9 |
21,7 |
25,6 |
0,3206 |
5,7 |
26,1 |
|
Крупные |
274,7 |
31,3 |
0,9203 |
421,7 |
11,4 |
30,2 |
0,9257 |
454,8 |
11,0 |
|
Все регионы |
128,5 |
31,3 |
0,9203 |
421,7 |
24,4 |
30,2 |
0,9257 |
454,8 |
23,5 |
|
2014 |
|||||||||
|
Малые |
122,1 |
19,4 |
0,9015 |
109,8 |
15,9 |
23,1 |
0,8601 |
73,8 |
18,9 |
|
Средние |
342,1 |
43,5 |
0,8044 |
49,4 |
12,7 |
59,0 |
0,6391 |
21,3 |
17,2 |
|
Крупные |
1034,5 |
198,0 |
0,888 |
83,2 |
19,1 |
235,2 |
0,8419 |
55,9 |
22,7 |
|
Все регионы |
479,0 |
120,2 |
0,9431 |
621,1 |
25,1 |
139,5 |
0,9233 |
451,3 |
29,1 |
Вышеприведенный анализ показателей для уравнений производственных функций линейного вида (параметров, статистических характеристик, предельных норм взаимозаменяемости ресурсов) свидетельствует о целесообразности проведения такого анализа и полезности сформулированных выводов для принятия управленческих решений.
При всей ценности и приемлемости результатов, полученных на основе уравнений производственных функций линейного вида, следует исследовать и другие виды уравнений. В частности, нами построены и исследованы уравнения для производственных функций степенного вида. Величины параметров уравнений регрессии построенных нами производственных функций степенного вида для обеих зависимостей (Y от K, L и Y от L, I) приведены в табл. 5.
Параметр (b) в случае степенной зависимости экономического смысла не имеет. Но параметры при переменных (т.е. показатели степеней) всегда имеют экономический смысл. Это обусловлено тем, что параметры в степенных уравнениях равны показателям, называемым коэффициентами эластичности 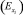 , рассчитываемыми по формуле
, рассчитываемыми по формуле
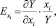
где 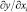 – предельная эффективность i-го показателя-фактора; xi – величина i-го показателя-фактора. В случае степенной зависимости
– предельная эффективность i-го показателя-фактора; xi – величина i-го показателя-фактора. В случае степенной зависимости 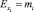 , т.е. представляют собой числовые величины, во всех остальных видах уравнений регрессии
, т.е. представляют собой числовые величины, во всех остальных видах уравнений регрессии 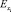 является переменной величиной, выражаемой вышеприведенной формулой его определения [1, 4, 5].
является переменной величиной, выражаемой вышеприведенной формулой его определения [1, 4, 5].
В уравнениях производственных функций степенного вида показатели степенной (коэффициенты эластичности) можно складывать (m1 + m2 и m2 + m3). При этом суммарные величины представляют собой величины роста результативного показателя в процентах при одновременном увеличении на 1 % обоих ресурсов, входящих в уравнение. Полученная сумма может быть больше, меньше или равна единице. Если сумма коэффициентов эластичности больше единицы, то говорят об эффекте масштаба, если меньше единицы, то – об отсутствии эффекта масштаба.
Анализ величин m1 + m2 и m2 + m3 из табл. 3 показывает отсутствие эффекта масштаба по обоим видам зависимостей (Y от K, L и Y от L, I) во всех трех группах регионов за все три рассматриваемых временных периода. Но такой эффект имеет место в целом по всем регионам за все рассматриваемые временные периоды. При этом по уравнениям обоих зависимостей Y от K, L и Y от L, I эффект масштаба оказался в 2005 г. максимальным, а в 2010 г. минимальным.
По табл. 5 сформулируем ряд важных, с нашей точки зрения, выводов:
– величины коэффициентов эластичности для зависимости Y и K, L показывают, что, во-первых, прирост производительности труда за счет увеличения стоимости основных фондов значительно выше, чем от увеличения численности работников; во-вторых, с ростом размеров регионов эластичность фондов повышается, а эластичность труда уменьшается; в-третьих, коэффициент эластичности основных фондов в 2014 г. по сравнению с 2005 г. значительно снизился, а эластичности труда – вырос;
Таблица 5
Величины параметров уравнений производственных функций степенного вида, выражающих зависимость ВРП (Y) от стоимости основных фондов (K), численности занятых в экономике (L) и объема инвестиций (I) по группам регионов России за 2005, 2010 и 2014 гг.
|
ВРП от стоимости основных фондов и численности занятых в экономике |
ВРП от численности занятых в экономике и инвестиций |
|||||
|
m1 |
m2 |
m1 + m2 |
m2 |
m3 |
m2 + m3 |
|
|
2005 |
||||||
|
Малые |
0,7306 |
0,0902 |
0,8208 |
0,5163 |
0,4555 |
0,9718 |
|
Средние |
0,7715 |
–0,0533 |
0,7182 |
0,3618 |
0,3678 |
0,7296 |
|
Крупные |
0,9975 |
–0,0350 |
0,9625 |
0,2877 |
0,6928 |
0,9805 |
|
Все регионы |
0,9309 |
0,1063 |
1,0372 |
0,5373 |
0,5257 |
1,0630 |
|
2014 |
||||||
|
Малые |
0,5518 |
0,2795 |
0,8313 |
0,4926 |
0,3329 |
0,8255 |
|
Средние |
0,5486 |
0,3817 |
0,9303 |
0,3030 |
0,4397 |
0,7427 |
|
Крупные |
0,6672 |
0,2636 |
0,9308 |
0,2718 |
0,6238 |
0,8956 |
|
Все регионы |
0,7143 |
0,3186 |
1,0329 |
0,3752 |
0,6563 |
1,0315 |
– в соответствии с уравнениями для зависимости Y от K, L эластичность труда по малым и средним регионам ниже, чем по крупным, и ниже, чем эластичность инвестиций; во-вторых, коэффициенты эластичности труда по малым и средним регионам в 2014 г. по сравнению с 2005 г. выросли, а по крупным – уменьшились;
– в целом по всем регионам России эластичность основных фондов и инвестиций в 2014 г. по сравнению с 2005 г. уменьшилась, а эластичность труда – увеличилась.
Анализ трех наиболее значимых статистических характеристик (коэффициента детерминации (R), F-критерия Фишера, средней ошибки аппроксимации (A)) для уравнений производственных функций степенного вида позволяет сформулировать ряд выводов. В частности, по величинам средней ошибки аппроксимации все рассматриваемые зависимости степенного вида можно считать «хорошими» (во всех случаях A < 10 %). Отметим также, что средняя ошибка аппроксимации по уравнениям производственных функций степенного вида значительно (в разы) меньше, чем по уравнениям линейного вида.
Несмотря на определенные преимущества уравнения степенного вида, считаем целесообразным и оправданным построение, оценку и применение обоих видов уравнений (линейного и степенного видов).
В заключение отметим, что в рамках проведенного исследования нами разработана и реализована на ПЭВМ компьютерная модель, позволяющая автоматизировать все расчеты и процедуры обработки информации, а также формировать весь комплекс аналитических таблиц для любых групп регионов за любой временной период.
Библиографическая ссылка
Адамадзиев К.Р., Халилов М.А. МОДЕЛИ ПРОИЗВОДСТВЕННЫХ ФУНКЦИЙ РЕГИОНОВ: РАСЧЕТ ПАРАМЕТРОВ И ХАРАКТЕРИСТИК, АНАЛИЗ ЗАВИСИМОСТИ ВЫПУСКА ПРОДУКЦИИ ОТ ЗАТРАТ РЕСУРСОВ // Фундаментальные исследования. 2016. № 4-2. С. 339-345;URL: https://fundamental-research.ru/ru/article/view?id=40178 (дата обращения: 12.07.2025).



