Обеспечение адаптивности газотурбинных авиационных двигателей (ГТД) к внешними и внутренним возмущениям (помехам) ведется средствами систем автоматического управления с обратными связями (САУ ГТД), для повышения эффективности которых применяются встроенные математические модели (ММ). В целях обеспечения надежности и безопасности работы модель должна быть адаптирована к нормальным деградационным (старение) и аномальным (отказы) процессам в двигателе, датчиках и исполнительных механизмах (ИМ) обратной связи САУ.
Авиационный двигатель является сложной динамической системой, уравнения состояния которой определяются как регулярной составляющей нестационарного процесса изменения параметров двигателя, так и случайным разбросом его характеристик. Разброс характеристик узлов двигателя и ИМ САУ определяется: техническим разбросом параметров, обусловленным допусками на изготовление и сборку узлов; отклонением в подобии режимов при различных внешних условиях эксплуатации; изменением характеристик в процессе наработки ресурса (отказы и старение узлов) и др. Сложность рассматриваемого объекта обусловливает трудности его идентификации при моделировании. В зависимости от решаемой задачи используются математические модели различного уровня детализации и точности.
Широкое практическое применение имеют термодинамические нелинейные математические модели высокого уровня, описывающие физические процессы в каждом компоненте двигателя. Такие модели наиболее полно отражают статические и динамические свойства двигателей как объектов управления во всем диапазоне рабочих режимов и служат основой для построения моделей низшего уровня. Основным достоинством этих моделей является высокая точность воспроизведения характеристик двигателя по всем параметрам реального рабочего процесса в диапазоне частот, определяемой частотой пропускания устройств автоматики. Основным недостатком, стимулирующим процесс дальнейшего поиска оптимальных решений задачи идентификации, является значительная сложность модели и ее зависимость от различного рода внешних и внутренних помех. В частности, для учета отклонений параметров ГТД от средних значений, заложенных в детерминированную модель, необходимо моделировать процессы в некоторой возможной области, обусловленной технологическим разбросом параметров. В то же время, для учета отклонений, вызванных внутренней и внешней неравномерностью потока газа в двигателе, необходимо в модель вносить шумы с заданными вероятностными характеристиками. Кроме того, на их качество влияет погрешность, связанная с неточностью задания физических констант. Следует также учитывать вероятные изменения характеристик двигателя вследствие старения. Большинства перечисленных проблем можно избежать, используя имитационные регрессионные модели, построенные на основе данных натурного эксперимента, производимого над отдельными узлами ГТД.
Цель исследования
Целью исследования является разработка регрессионной математической модели ИМ САУ ГТД с разделением влияния факторов методом полиномиальной аппроксимации.
Материалы и методы исследования
В предлагаемом исследовании строится математическая модель нижнего уровня исполнительного механизма обратной связи САУ ГТД – гидропривода входных направляющих аппаратов компрессора (ВНА) ГТД с помощью регрессионного анализа. Выбранный метод идентификации основан на регрессионной процедуре с использованием метода наименьших квадратов и применяется для описания нестационарных процессов, характеризующихся медленным (по сравнению с регрессией) изменением параметров, а также для полиномиальной аппроксимации неизвестных нелинейных функций.
Рассматриваемый объект является астатическим и в первом приближении описывается дифференциальным уравнением второго порядка:
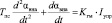 , (1)
, (1)
где Iупр – входной сигнал гидропривода (входной ток преобразователя электрических сигналов (ПС)), мА; αвна – выходной сигнал гидропривода (угол поворота ВНА), град; Тпс – постоянная времени ПС, сек; Kгм – коэффициент усиления гидропривода. Причем
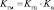 ;
; 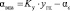 , (2)
, (2)
где Kгц – коэффициент усиления гидроцилиндра гидропривода; Kα – коэффициент усиления устройства поворота ВНА; αo – угол установки механического упора, град; yгц – выходной сигнал гидроцилиндра гидропривода, мм.
Реальная система является нелинейной и характеризуется наличием силы трения в полости поршня гидроцилиндра; магнитного гистерезиса; люфта в цепи обратной связи; гидродинамических сил, переменных по величине расхода, возникающих в дозирующем сечении; реакции струи из сопла на заслонку, обусловленной возможной несимметричностью сопл преобразователя электрических сигналов (Iпс), поступающих на вход гидропривода с выхода регулятора и т.д. Действие этих возмущений обусловливает трансформации скоростной характеристики гидропривода, задающей экспериментально полученную функцию скорости перемещения гидроцилиндра на выходе устройства от тока управления 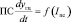 , задаваемую графически или таблично.
, задаваемую графически или таблично.
В предлагаемой методике идентификации скоростная характеристика выступает как обобщенная характеристика рассматриваемого ИМ, и построение модели исследуемого объекта сводится к ее полиномиальной аппроксимации. Под действием различного рода возмущений (помех) на скоростной характеристике наблюдается появление зоны нечувствительности, параллельное смещение характеристики относительно начала координат, сужение линейной зоны. Для исследования рассматривалось изменение силы трения (Fтр) в полости поршня гидроцилиндра; изменение величины давления в клапане постоянного давления (Pкпд), например вследствие поломки насоса; изменения площади открытия сопл (fс1 и fс2), задающих перепад давления на золотнике преобразователя входных электрических сигналов; изменения жесткости пружины золотника (Cпр) вследствие нарушения ее затяжки. В ходе работы был сделан вывод о возможности ограничения этим списком, так как действие всех прочих возмущений аналогично перечисленным.
В качестве исходных данных при построении модели исследуемого объекта использовались результаты натурных и модельных экспериментов. С целью повышения достоверности модельного эксперимента в построенной нелинейной модели высшего уровня изменения параметров задавались различными законами распределения (нормальным, равномерным и др.) с учетом технологических допусков изготовителей. Суммарная относительная дисперсия, соответствующая технологическим нормам, составляет D = ∑Di = 0,1189.
Скорректированная таким образом модель использовалась для получения скоростных характеристик номинального режима работы гидропривода и режимов, соответствующих всем перечисленным возмущениям с выборкой N = 200. Фиксированное значение тока ПС задавалось в диапазоне [– 35 mA; + 35 mA]. При этом все параметры гидропривода изменялись в соответствии с заданными законами распределения в пределах заданных отклонений. Полученные семейства из 200 кривых, соответствующие каждому случаю действия возмущения, подверглись статистической обработке.
Проведенные расчеты позволили сделать вывод о возможности выбора в качестве истинного значения измеряемой величины среднего арифметического результатов наблюдений. Полученные регрессионные характеристики были сгруппированы в семейства кривых, соответствующие случаю действия каждого рассмотренного возмущения.
Предлагаемая модель с разделением влияния факторов для рассматриваемого ИМ основана на полиномиальной аппроксимации полученных скоростных характеристик. В соответствии с методом линейной регрессии наилучшие значения для коэффициентов аппроксимационного полинома можно определить из матричного уравнения:
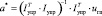 , (3)
, (3)
где а* = (а0а1…аn)Т – матрица наилучших коэффициентов аппроксимационного полинома; n – степень апроксимационного полинома; Iупр – матрица токов управления ПС; uгц – матрица выходных сигналов, соответствующих 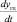 .
.
Результаты исследования и их обсуждение
Выбор степени полинома был осуществлен для скоростной характеристики, соответствующей номинальному режиму. На основе анализа скоростной характеристики ИМ, можно предположить, что порядок полинома должен быть достаточно высок, поэтому в исследовании рассмотрен вариант разбиения исходной функции на два участка, соответствующих интервалам изменения аргумента Iупр∈ [– 35 mA; 0] и Iупр∈ [0; + 35 mA]. При использовании описанной регрессионной процедуры получены полиномы степеней n = 4, а также рассчитаны соответствующие им дисперсии D = 0,0477 и 0,0295, характеризующие отклонение экспериментальных результатов от модельных значений. Сравнение с результатами произведенной аппроксимации полиномами Лагранжа показало, что точность результата для n = 5 улучшилась в два раза. Таким образом, был сделан вывод о целесообразности применения рассматриваемого метода при пятой степени полинома для номинального режима работы ИМ. Осциллограмма полученной функции приведена на рис. 1.
Учет действия возмущений в построенной модели для номинального режима производится путем введения корректирующих коэффициентов в виде полиномов третьей степени:
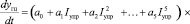
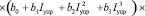
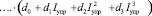 , (4)
, (4)
где ao, …, a5 – коэффициенты полинома, описывающего номинальный режим работы ИМ; bo, …, b3; ….; do, … , d3 – коэффициенты полиномов, описывающих соответственно режимы работы ИМ в условиях действия помех: изменения жесткости пружины золотника Cпр, изменения величины давления в клапане постоянного давления Pкпд, изменения силы трения Fтр в полости поршня гидроцилиндра и изменения площади открытия сопла fс1, задающего перепад давления на золотнике преобразователя входных электрических сигналов.
Корректирующие полиномы определены для всех выбранных возмущений, графическое отображение влияния которых на форму скоростной характеристики ИМ отражено на осциллограмме проведенного натурного эксперимента (рис. 2).
Экспериментальные исследования показали, что корректирующие коэффициенты существенно отличаются на различных диапазонах изменения параметра, задающего действие помехи, что обусловлено необходимостью определения законов изменения каждого корректирующего коэффициента для каждого полинома на нескольких участках изменения исследуемого параметра (Cпр, Pкпд, Fтр, fс1). Для определения коэффициентов bi, …, di с целью уменьшения погрешности использовалась сплайн-интерполяция. Диапазон изменения авсциссы (тока управления ПС) также разбивался на более мелкие, чем для номинального режима, промежутки. Так, например, при моделировании изменения затяжки пружины Cпр в диапазоне ее изменения от 0,4 Cпр ном до 2 Cпр ном, корректирующие коэффициенты определялись на двух участках изменения жесткости пружины Cпр ∈ [0,4; 0,8] ∪ [0,8; 2] и на шести участках изменения тока Iупр в пределах диапазона [– 35 mA; + 35 mA].
В результате проведенной идентификации были получены матрицы коэффициентов корректирующих полиномов, соответствующих изменению параметров, характеризующих действие различных помех, в заданных диапазонах.
Следует отметить, что для случая изменения Pкпд и fс1 особенностью нахождения коэффициентов корректирующего полинома является необходимость исключения постоянной составляющей в исходных данных, наличие которой приводит к параллельному смещению графиков функций вдоль координатных осей относительно номинального положения. Для этого определялся закон изменения константы (постоянной составляющей). Кривые скоростных характеристик, построенных с помощью разработанной регрессионной модели с разделением влияния факторов, приведены на рис. 3.
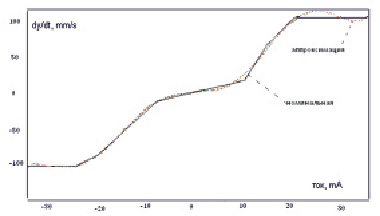
Рис. 1. Осциллограмма результатов полунатурного эксперимента по полиномиальной аппроксимации номинальной скоростной характеристики

Рис. 2. Осциллограмма результатов натурного эксперимента по определению трансформаций скоростной характеристики ВНА при различных видах помех
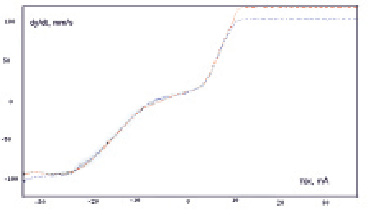
Рис. 3. Осциллограмма результатов модельного эксперимента по учету влияния помех путем введения корректирующих полиномиальных коэффициентов
Выводы
Сравнительный анализ полученных результатов показал, что построенная регрессионная модель входных направляющих аппаратов компрессора с разделением влияния факторов (помех) имеет более высокие показатели точности, чем аналогичные модели, разработанные с применением других методов аппроксимации. Разработанная модель применима как в статическом, так и в динамическом режиме в условиях действия нескольких помех. Характеристики помех могут задаваться или изменяться по случайному закону в указанном диапазоне.
Разработанная модель может применяться как в стендовом оборудовании для наземных испытаний ГТД, так и в бортовых моделях двигателя всех уровней.
Библиографическая ссылка
Кузнецова Т.А. РЕГРЕССИОННЫЕ МАТЕМАТИЧЕСКИЕ МОДЕЛИ ПОДСИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ АВИАЦИОННЫМ ДВИГАТЕЛЕМ С РАЗДЕЛЕНИЕМ ВЛИЯНИЯ ФАКТОРОВ // Фундаментальные исследования. 2016. № 2-2. С. 271-275;URL: https://fundamental-research.ru/ru/article/view?id=39921 (дата обращения: 19.01.2026).



