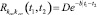Повышение точности силовых приводов, являющихся важной частью систем автоматического управления и применяемых в таких областях, как авиация, ракетостроение, робототехника, транспортное машиностроение, энергетика, является актуальной проблемой. В большинстве подобных приложений используется электрогидравлический следящий привод (ЭГСП), обладающий высокой удельной мощностью и быстродействием [2]. В то же время для ЭГСП характерна заметная чувствительность к свойствам рабочей жидкости, температуре окружающей среды, технологическому разбросу параметров и другим факторам, носящим в основном случайный характер. Влияние вышеуказанных факторов может быть учтено введением случайных параметров в математическую модель ЭГСП, используемую на этапе разработки в качестве основы всех расчетных процедур. В связи с этим актуальной является задача построения более адекватных математических моделей, в которых ЭГСП рассматривается как стохастическая система управления. При этом возникает задача идентификации случайных параметров данных математических моделей.
С другой стороны, переход к классу стохастических систем ведет к усложнению математических моделей и требует новых методов решения традиционных задач анализа и идентификации. При этом в большинстве практических случаев невозможно получение точных аналитических решений, что делает актуальной задачу разработки приближенных вычислительных методов, ориентированных на эффективную программную реализацию. Среди таких методов набирают возрастающую популярность проекционные методы, называемые также спектральными. В отечественной литературе им посвящен ряд монографий, например, [9], [8], [1], ставших классическими в области применения проекционных методов для решения задач теории автоматического управления, а также [6], [4], [3]. Универсальность проекционных методов демонстрирует их приложение к современным задачам математической физики [7].
Целью настоящей работы является исследование возможностей применения проекционных методов [6] и аппарата матричных операторов [1] для решения задачи идентификации статистических характеристик случайных параметров математической модели ЭГСП.
Задача идентификации случайных параметров
Общей формой математической модели класса стохастических систем, к которому относится ЭГСП, является дифференциальное уравнение вида
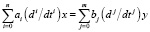 ;
; 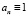 , (1)
, (1)
где все или некоторые коэффициенты ai и bj являются случайными величинами, определяемыми как
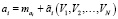 ,
, 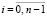 ,
,
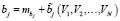 ,
, 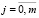 , (2)
, (2)
где 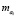 ,
, 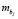 – математические ожидания случайных коэффициентов ai, bj;
– математические ожидания случайных коэффициентов ai, bj; 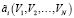 ,
, 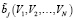 – центрированные случайные величины, линейно зависящие от случайных величин V1, V2, …, VN. При этом случайные величины V1, V2, …, VN статистически независимы, имеют нормальный закон распределения плотности вероятности с нулевым математическим ожиданием и единичной дисперсией.
– центрированные случайные величины, линейно зависящие от случайных величин V1, V2, …, VN. При этом случайные величины V1, V2, …, VN статистически независимы, имеют нормальный закон распределения плотности вероятности с нулевым математическим ожиданием и единичной дисперсией.
Система автоматического управления (ЭГСП), описываемая моделью (1), имеет N случайных параметров, которые можно представить как случайные коэффициенты полиномов числителя и знаменателя передаточных функций динамических звеньев на ее структурной схеме. Данные коэффициенты имеют определенный физический смысл, соответствующую размерность и представляются в виде
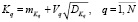 , (3)
, (3)
где 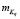 и
и 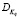 – математическое ожидание и дисперсия q-го случайного параметра. В свою очередь, случайные коэффициенты ai и bj модели (1) выражаются через случайные параметры Kq, то есть представляются как ai(K1, K2,... KN), bj(K1, K2,... KN) что, в конечном итоге, соответствует их представлению в виде (2).
– математическое ожидание и дисперсия q-го случайного параметра. В свою очередь, случайные коэффициенты ai и bj модели (1) выражаются через случайные параметры Kq, то есть представляются как ai(K1, K2,... KN), bj(K1, K2,... KN) что, в конечном итоге, соответствует их представлению в виде (2).
Задача идентификации случайных параметров формулируется следующим образом. Для системы управления с N случайными параметрами Kq, математическая модель которой описывается дифференциальным уравнением (1), требуется найти дисперсии этих случайных параметров 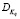 . При этом предполагается, что данные параметры имеют нормальный закон распределения и их математические ожидания
. При этом предполагается, что данные параметры имеют нормальный закон распределения и их математические ожидания 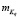 являются известными. Также предполагается выполнение условия физической реализуемости системы управления, формулируемого как n > m в (1).
являются известными. Также предполагается выполнение условия физической реализуемости системы управления, формулируемого как n > m в (1).
Если случайные параметры системы являются переменными, то есть заметно изменяются на интервале исследования и, таким образом, представляют собой случайные процессы, то вместо представления (3) может быть использовано представление
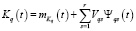 ,
, 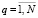 , (4)
, (4)
построенное на основе канонического разложения, позволяющего представить случайные процессы Kq(t) в виде линейной комбинации независимых случайных величин Vqs (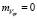 ,
, 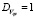 ), являющихся коэффициентами канонических разложений этих случайных процессов по системам неслучайных координатных функций Ψqs(t). Данные координатные функции, в свою очередь, определяются через соответствующие корреляционные функции
), являющихся коэффициентами канонических разложений этих случайных процессов по системам неслучайных координатных функций Ψqs(t). Данные координатные функции, в свою очередь, определяются через соответствующие корреляционные функции 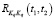 . Алгоритм вычисления координатных функций Ψqs(t) проекционным методом с использованием разложения Холецкого можно найти в [6, с. 126–128].
. Алгоритм вычисления координатных функций Ψqs(t) проекционным методом с использованием разложения Холецкого можно найти в [6, с. 126–128].
При такой постановке задачи идентификации математическое ожидание 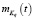 и вид корреляционных функций
и вид корреляционных функций 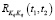 случайных параметров системы управления предполагаются известными, а идентификации подлежат только параметры корреляционных функций
случайных параметров системы управления предполагаются известными, а идентификации подлежат только параметры корреляционных функций 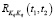 , т.е. элементы вектора
, т.е. элементы вектора 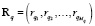 в параметризованном представлении
в параметризованном представлении 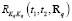 .
.
Для решения задачи идентификации необходимо иметь информацию о входном и выходном сигнале системы. Эту информацию можно получить непосредственным измерением этих сигналов, используя результаты лабораторных или практических исследований системы при подаче на ее вход некоторых известных воздействий. Исходными данными для решения задачи идентификации в вышеуказанной постановке являются математическое ожидание mx(t) и корреляционная функция Rxx(t1, t2) выходного сигнала системы, которые определяются в результате усреднения ее выходного сигнала x(t) по множеству реализаций.
Алгоритм идентификации
Предлагаемый алгоритм идентификации основан на минимизации критерия, зависящего от дисперсий параметров модели. В качестве такого критерия выбрана мера близости корреляционных функций и функций математического ожидания измеренного выходного сигнала реальной системы и тех же статистических характеристик, вычисленных по ее параметризованной модели, выражаемая следующим функционалом:
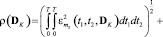
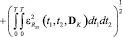 , (5)
, (5)
где 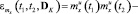
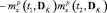 ,
,
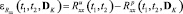 ,
,
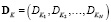 – вектор дисперсий случайных параметров модели; верхним индексом «u» отмечены измеренные, а индексом «p» – расчетные статистические характеристики выходного сигнала системы.
– вектор дисперсий случайных параметров модели; верхним индексом «u» отмечены измеренные, а индексом «p» – расчетные статистические характеристики выходного сигнала системы.
Определенной проблемой является вычисление 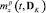 и
и 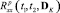 , входящих в (5). При этом важно не только выбрать метод вычисления данных статистических характеристик, но и обеспечить высокую эффективность вычислительного алгоритма, построенного на его основе. Особенностью подхода, предлагаемого в данной работе, является использование проекционной аппроксимации исходной непрерывной модели (1) по методике, описанной в [6, с. 98–129], и аппарата матричных операторов [1]. При этом удается построить параметризованную модель стохастической системы, которая в операторной форме устанавливает связь статистических характеристик входа, выхода и случайных параметров, демонстрируя относительную эффективность при вычислении функционала (5) по сравнению с методом статистических испытаний.
, входящих в (5). При этом важно не только выбрать метод вычисления данных статистических характеристик, но и обеспечить высокую эффективность вычислительного алгоритма, построенного на его основе. Особенностью подхода, предлагаемого в данной работе, является использование проекционной аппроксимации исходной непрерывной модели (1) по методике, описанной в [6, с. 98–129], и аппарата матричных операторов [1]. При этом удается построить параметризованную модель стохастической системы, которая в операторной форме устанавливает связь статистических характеристик входа, выхода и случайных параметров, демонстрируя относительную эффективность при вычислении функционала (5) по сравнению с методом статистических испытаний.
Проекционная аппроксимация модели (1) позволяет представить функционал (5) в следующей форме:
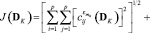
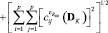 , (6)
, (6)
где 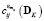 и
и 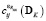 – элементы квадратных матриц проекционных характеристик
– элементы квадратных матриц проекционных характеристик 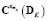 и
и 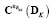 соответственно, вычисляемых как
соответственно, вычисляемых как
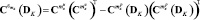 ,
,
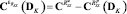 ,
,
где 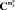 – проекционная характеристика функции математического ожидания измеренного выходного сигнала системы
– проекционная характеристика функции математического ожидания измеренного выходного сигнала системы 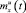 ;
; 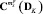 – расчетная проекционная характеристика математического ожидания выходного сигнала системы, вычисленная по ее усредненной проекционной модели для некоторого значения дисперсий случайных параметров DK;
– расчетная проекционная характеристика математического ожидания выходного сигнала системы, вычисленная по ее усредненной проекционной модели для некоторого значения дисперсий случайных параметров DK; 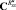 – проекционная характеристика корреляционной функции измеренного выходного сигнала системы
– проекционная характеристика корреляционной функции измеренного выходного сигнала системы 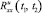 ;
; 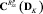 – расчетная проекционная характеристика корреляционной функции выходного сигнала системы, вычисленная по ее усредненной проекционной модели для некоторого значения дисперсий случайных параметров DK; T – знак транспонирования.
– расчетная проекционная характеристика корреляционной функции выходного сигнала системы, вычисленная по ее усредненной проекционной модели для некоторого значения дисперсий случайных параметров DK; T – знак транспонирования.
Усредненная проекционная модель, используемая при вычислении функционала (6), в операторной форме устанавливает связь между статистическими характеристиками входа, выхода и случайных параметров системы автоматического управления, описываемой моделью (1). Методика построения такой модели, основанная на приеме приближенного представления случайной матрицы оператора стохастической системы матричным рядом, подробно описана в [6, с. 98–129]. Операция усреднения данной случайной матрицы при решении задачи анализа [6, с. 129–139] сводится к аналитическим операциям независимого усреднения членов упомянутого матричного ряда, которое, в свою очередь, сводится к усреднению различных степеней случайных величин 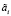 ,
, 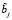 и, в конечном итоге, различных степеней случайных величин Vq в (3) или Vqs в (4), то есть к вычислению стохастических моментов различных порядков с использованием соответствующих алгоритмов символьных преобразований, что также позволяет автоматически учитывать возможное наличие жесткой статистической связи между коэффициентами уравнения (1) через случайные величины V1, V2, …, VN.
и, в конечном итоге, различных степеней случайных величин Vq в (3) или Vqs в (4), то есть к вычислению стохастических моментов различных порядков с использованием соответствующих алгоритмов символьных преобразований, что также позволяет автоматически учитывать возможное наличие жесткой статистической связи между коэффициентами уравнения (1) через случайные величины V1, V2, …, VN.
Таким образом, решением задачи идентификации будет
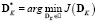 . (7)
. (7)
Функционал (6) является проекционным аналогом функционала (5). Минимизацию данного функционала целесообразно выполнять одним из методов прямого поиска, например, методом Нелдера-Мида.
Представление (4) позволяет использовать описанный алгоритм для идентификации переменных случайных параметров за счет расширения системы независимых случайных величин V1, V2, …, VN в представлении (2) до (V11, V12, …, V1r), (V21, V22, …, V2r), … (Vq1, Vq2, …, Vqr). При этом вектор RK = (R1, R2, …, RN) заменяет вектор DK в (6) и (7).
Пример идентификации переменного случайного параметра
В качестве исходной математической модели ЭГСП рассматривается линеаризованная модель 8-го порядка, которая описывается следующей системой дифференциальных уравнений:
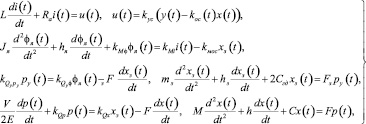 (8)
(8)
где y(t) – электрическое напряжение на суммирующем входе электронного усилителя сигнала ошибки (входной сигнал ЭГСП); u(t) – напряжение на обмотке управления электромеханического преобразователя (ЭМП); i(t) – ток в обмотке управления ЭМП; φя(t) – угол поворота якоря ЭМП и закреплённой на нем заслонки; py(t) – перепад давления на торцах золотника электрогидравлического усилителя (ЭГУ); хз(t) – перемещение золотника ЭГУ; р(t) – перепад давления в полостях гидроцилиндра; x(t) – перемещение штока поршня гидроцилиндра (выходной сигнал ЭГСП).
Коэффициенты уравнений модели (8) имеют традиционный физический смысл, подразумеваемый для подобных математических моделей, описанных, например, в [5]. В качестве случайного параметра рассматривается переменный коэффициент электрической обратной связи koc(t), представляемый в виде гауссова случайного процесса, то есть K1(t) = koc(t) в представлении (4). Вид его корреляционной функции считается известным:
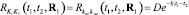 ,
,
а математическое ожидание – постоянным: 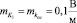 . Идентификации подлежат параметры, составляющие вектор R1 = (r11, r12), где r11 = D, r12 = b. Согласно исходной модели (8) от данного случайного параметра зависит коэффициент a0 в (1), где n = 8 и m = 0, который также являются гауссовым случайным процессом a0(t). Проекционная аппроксимация модели (1) выполнялась в базисе функций Уолша с удержанием 64 членов разложения.
. Идентификации подлежат параметры, составляющие вектор R1 = (r11, r12), где r11 = D, r12 = b. Согласно исходной модели (8) от данного случайного параметра зависит коэффициент a0 в (1), где n = 8 и m = 0, который также являются гауссовым случайным процессом a0(t). Проекционная аппроксимация модели (1) выполнялась в базисе функций Уолша с удержанием 64 членов разложения.
Для исследования возможностей применения предлагаемого алгоритма идентификации был выполнен вычислительный эксперимент, в котором параметры D и b корреляционной функции случайного процесса koc(t) считались известными и выступали в качестве эталонных значений, позволяющих оценить точность решения задачи идентификации. В ходе данного эксперимента сначала решалась задача статистического анализа ЭГСП методом статистических испытаний с использованием проекционного аналога модели (8) для заданных значений D = 0,0005 и b = 1, в результате чего находились матрицы 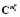 и
и 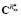 , необходимые для вычисления функционала (6). При принятом числе испытаний 2000 доверительная вероятность и относительное отклонение оценок
, необходимые для вычисления функционала (6). При принятом числе испытаний 2000 доверительная вероятность и относительное отклонение оценок 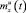 ,
, 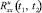 составляли не менее 0,9 и не более 0,05 соответственно. Затем решалась задача идентификации путем минимизации функционала (6) методом Нелдера-Мида в соответствии с (7), в результате чего идентифицировались значения D и b, которые сравнивались с заданными эталонными. Результаты для разных интервалов времени моделирования 0..T представлены в таблице. Для каждого идентифицированного значения в нижней половине соответствующей клетки таблицы приводится величина относительной погрешности идентификации, выраженная в процентах.
составляли не менее 0,9 и не более 0,05 соответственно. Затем решалась задача идентификации путем минимизации функционала (6) методом Нелдера-Мида в соответствии с (7), в результате чего идентифицировались значения D и b, которые сравнивались с заданными эталонными. Результаты для разных интервалов времени моделирования 0..T представлены в таблице. Для каждого идентифицированного значения в нижней половине соответствующей клетки таблицы приводится величина относительной погрешности идентификации, выраженная в процентах.
Результаты идентификации
|
Т, с |
Идентифицированные параметры корреляционной функции |
|||||
|
Погрешность измерения выходного сигнала [ %] |
||||||
|
10 % |
5 % |
1 % |
||||
|
D |
b |
D |
b |
D |
b |
|
|
0,7 |
0,00047 |
1,1294 |
0,00056 |
1,0082 |
0,00055 |
0,9937 |
|
6 % |
13 % |
12 % |
1 % |
10 % |
0,6 % |
|
|
0,3 |
0,00051 |
1,160 |
0,00049 |
0,9761 |
0,00050 |
0,9512 |
|
2 % |
15 % |
2 % |
2 % |
0,03 % |
5 % |
|
В данном вычислительном эксперименте дополнительно проверялось влияние погрешности измерения выходного сигнала ЭГСП на точность идентификации. Эта погрешность представлялась в виде аддитивного белого шума, наложенного на выходной сигнал. Шум имел нормальный закон распределения, нулевое математическое ожидание и среднеквадратическое отклонение 1 %, 5 % и 10 % от амплитуды измеряемого сигнала у(t). Результаты моделирования демонстрируют относительную устойчивость рассматриваемого алгоритма идентификации к ошибкам измерения выходного сигнала ЭГСП.
Заключение
Применение проекционных методов и аппарата матричных операторов позволило предложить эффективный вычислительный алгоритм идентификации случайных физических параметров математической модели электрогидравлического следящего привода, основанный на использовании усредненной проекционной модели стохастической системы и оптимизационной процедуры. Матрично-операторная форма записи решений, характерная для проекционных методов, дает возможность построить удобный для вычисления функционал, минимизация которого обеспечивает определение статистических характеристик идентифицируемых случайных параметров. Пример идентификации переменного случайного параметра математической модели 8-го порядка демонстрирует возможность применения предлагаемого алгоритма для нередуцированных моделей реальных технических объектов.
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований и Правительства Калужской области (грант № 14-41-03071).
Библиографическая ссылка
Аунг Чжо Со, Макаренков А.М., Мьо Паинг Сат ИДЕНТИФИКАЦИЯ СЛУЧАЙНЫХ ПАРАМЕТРОВ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ЭЛЕКТРОГИДРАВЛИЧЕСКОГО СЛЕДЯЩЕГО ПРИВОДА // Фундаментальные исследования. 2016. № 2-2. С. 231-235;URL: https://fundamental-research.ru/ru/article/view?id=39913 (дата обращения: 21.01.2026).