Моделирование и расчет аппаратов и установок составляют один из основных этапов внедрения технологического оборудования в производственный процесс. Простота методов моделирования и расчета сокращает время пуска технологической линии, что, в свою очередь, позволяет ускорить получение прибыли.
Методы кибернетики позволяют не только сократить путь перехода от лабораторного стола к промышленной реализации, но и резко уменьшить число необходимых опытов, быстро выявить оптимальный вариант осуществления изучаемого процесса. Кроме того, кибернетические методы моделирования можно считать универсальными для множества различных процессов. Использование передаточных функций позволяет описывать динамические свойства системы практически любой структуры и сложности. Единственный недостаток – полученное описание не отражает физические закономерности процесса. Однако именно это позволяет связать в единую систему модели различных процессов, различных по физической основе.
Кибернетический подход целесообразно использовать при описании мембранных методов. Достаточно актуальным является математическое моделирование процесса мембранного концентрирования в аппаратах с отводом поляризационного слоя [4].
В работе [5] предложена следующая методика разработки модели процесса:
1) выбор структуры модели по результатам изучения объекта по имеющимся сведениям;
2) выбор критерия близости (подобия) модели и объекта;
3) определение параметров модели по экспериментальным данным, исходя из критерия близости.
На первом этапе, исходя из описания мембранной установки, в соответствии с принципом «чёрного ящика» можно выделить основные каналы передачи сигналов с входов на выходы системы и представить её в следующем виде (рис. 1).
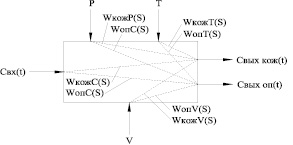
Рис. 1. Структурная схема мембранного аппарата
Основные каналы типа «вход – выход»:
– «исходная концентрация Свх(t) – концентрация раствора из кожуха Свых кож(t)» (Wкож(S));
– «исходная концентрация Свх(t) – концентрация основного потока Свых оп(t)» (Wоп(S)).
На систему также оказывают влияние основные технологические параметры: давление (Р), температура концентрируемого раствора (Т) и гидродинамическая обстановка в канале аппарата (критерий Рейнольдса, V) [4]. Передаточные свойства каждого канала системы определяются соответствующей передаточной функцией (рис. 1), обозначения которой имеют двойной индекс: первый отражает наименование выхода системы, второй – технологический входной параметр.
Следующий шаг – выбор вида и величины входных воздействий. Использование типовых («эталонных») воздействий позволяет унифицировать расчёты различных систем и облегчает сравнение передаточных свойств систем [1]. Для упрощения рекомендуется выбрать ступенчатое воздействие, при котором значение мгновенно возрастает от нуля до некоторой величины и далее остаётся постоянным.
Для процесса мембранного концентрирования теоретически существуют два способа выхода переменных в статический режим: при отсутствии диффузионного слоя на мембране и при его наличии. Однако отсутствие слоя подразумевает использование исходной жидкости без содержания сухих веществ, что не имеет место на практике. Поэтому в данном случае для определения реакции системы на то или иное воздействие (Т, Р, V) необходимо совместное нанесение соответствующего возмущения с возмущением по каналу «концентрация исходного раствора – выход».
После определения передаточных функций по каждому каналу можно записать итоговую модель процесса:
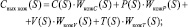 (1)
(1)
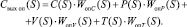 (2)
(2)
При известных входных воздействиях C(S) и P(S) по формулам (5) можно определить состояние выходов системы (для V(S) и T(S) формулы аналогичны).
Описанный метод моделирования был усовершенствован автором [3], которым были внесены следующие дополнения.
Входным воздействием является концентрация задерживаемых веществ в исходном растворе Свх(t), % масс. К выходным параметрам относятся: содержание растворенных веществ в концентрате, отводимом из кожуха Свых кож(t), % масс. и конуса Свых кон(t), % масс.; концентрация растворенных веществ в основном потоке Свых оп(t), % масс.; удельная производительность по фильтрату Gф(t), м3/(м2?с).
Таким образом было увеличено количество информационных связей, учитываемых в модели, и количество выходных параметров, полученных в результате применения данного метода моделирования.
Удельная производительность, являющаяся одним из выходов системы, изменяется со временем по экспоненциальному закону, ее можно описать зависимостью (3), которая представляет собой видоизмененную передаточную функцию апериодического звена второго порядка.
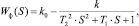 (3)
(3)
где k – коэффициент усиления объекта; Т1, Т2 – постоянные времени объекта; k0 – удельная производительность по фильтрату в начальный момент времени.
Удельная производительность для каждого из случаев совместного нанесения воздействий на моделируемую систему описывается зависимостями вида (4), откуда аналитически могут быть получены передаточные функции, отражающие динамику изменения проницаемости мембраны по фильтрату при воздействии каждого технологического параметра (например, по P(S) (5)).
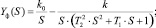 (4)
(4)
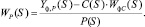 (5)
(5)
Итоговую модель объекта можно записать в виде системы (6).
Система (8) определяет состояние выходов объекта моделирования во времени при известной концентрации растворенных веществ в исходном растворе C(S), а также при определенных значениях технологических параметров процесса P(S), V(S) и Т(S).
Описанные модели обладают общим существенным недостатком – привязкой к конкретному конструктивному исполнению аппарата, что лишает их универсальности. В дальнейших разработках этот недостаток был устранен без снижения точности модели.
Так, авторами [7] была предложена следующая структурная схема мембранного концентрирования (рис. 2).
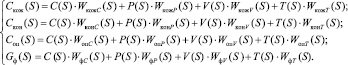 (6)
(6)
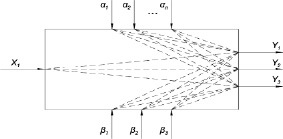
Рис. 2. Структурная схема мембранного концентрирования
В соответствии со структурной схемой (рис. 2) в данной модели учитывается влияние конструктивных параметров аппарата (подмножество α множества Х) и технологических режимов процесса (подмножество β множества Х). То есть множество входных контролируемых управляемых независимых переменных в данном случае может быть отражено выражением:
{X} = {X1, α1, α2, …, αn, β1, β2, …, βm}, (7)
где m – количество учитываемых технологических параметров; n – количество учитываемых конструктивных параметров аппарата. К выходным параметрам относятся: содержание растворенных веществ в отводимом примембранном пограничном слое Y1, % масс.; концентрация растворенных веществ в основном потоке Y2, % масс.; удельная производительность по фильтрату Y3, м3/м2?с.
Передаточные свойства каждого канала системы определяются соответствующей передаточной функцией (рис. 2), обозначения которой имеют двойной индекс: первый отражает входной параметр, второй – наименование выхода системы.
Итоговая модель имеет вид:
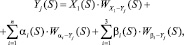
j = 1...3. (8)
Данная модель дополняет модели авторов [3, 5]. Она не привязана к конструктивным особенностям аппарата, а рассматривает влияние различных параметров на процесс концентрирования.
При дальнейшем изучении вопроса автором [8] были внесены усовершенствования предложенной выше модели. В качестве возмущающих воздействий, наряду с конструктивными и технологическими, было предложено внести режимные параметры.
Кроме того, представляет отдельный интерес моделирование поведения физико-химических показателей сырья в процессе его переработки. В связи с этим в модель включен компонент, позволяющий на основе эмпирических зависимостей производить расчет физико-химических показателей получаемого продукта (плотность, вязкость и др.). Они обозначены подмножеством:
{Q} = (Q1, ..., Qw), (9)
где w – количество физико-химических показателей продукта.
Таким образом, в соответствии с предложенной структурной схемой (рис. 3), на процесс концентрирования влияют технологические (подмножество α множества Х), конструктивные (подмножество β множества Х) и режимные (подмножество γ множества Х) параметры аппарата.
Итоговую модель объекта можно записать в виде.
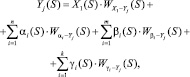
j = 1...3. (10)
Уравнение (10) определяет состояние выходов объекта моделирования во времени при известной концентрации задерживаемых веществ в исходном растворе X1(S), а также при определенных значениях параметров процесса концентрирования.
Исходя из изложенного, можно сделать вывод, что развитие математических моделей осуществляется по двум направлениям:
1. Дополнение моделей не учтенными ранее возмущающими воздействиями.
2. Получение дополнительных выходных параметров процесса.
При добавлении в модель новых информационных связей должна оставаться достаточно высокой или становиться ещё выше её точность и прогностическая способность.
Регулярно приходится сталкиваться с ситуациями, когда необходимо изменять значения возмущающих воздействий в результате несоответствия полученных значений выходных параметров диапазонам допустимых значений, либо приближения к границам этих диапазонов. Для таких случаев необходимо применять обратную связь. В связи с этим предложена следующая информационная схема (рис. 4) [6].
Сигналы, которыми производится корректировка возмущающих воздействий, обозначены f[1...k](Y). Диапазон допустимых значений обозначен множеством K, для каждого выходного воздействия множество задается отдельно.
Выбор входного воздействия и определение передаточных функций будет производиться аналогично описанным ранее моделям, но с поправкой на обратную связь.
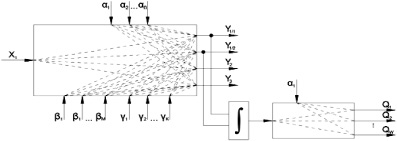
Рис. 3. Структурная схема процесса мембранного концентрирования
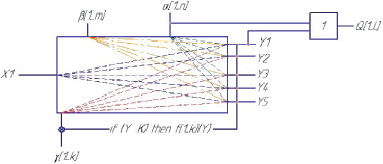
Рис. 4. Структурная схема процесса мембранного концентрирования
Итоговую модель объекта можно записать в виде.
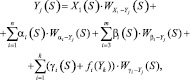 j = 1..5, k = 1...5. (11)
j = 1..5, k = 1...5. (11)
Для дальнейшего развития изложенных идей представляет интерес последовательное объединение информационных моделей объектов в соответствии с технологической схемой производства, что позволит моделировать всю производственную линию от поступления сырья до получения готового продукта. При этом при выборе отслеживаемых выходных параметров следует учитывать необходимые входные параметры и возбуждающие воздействия следующих ступеней производства. В результате такого моделирования могут быть получены математические модели для информационных схем, соответствующих целым участкам или линиям производства (рис. 5).
Последовательная обработка каждого звена информационной схемы и построение передаточных функций для каждой, с учетом их взаимосвязей и линий обратной связи позволит построить математическую модель для завершенного технологического процесса.
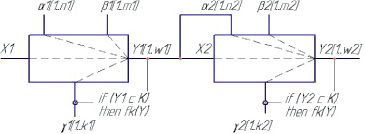
Рис. 5. Общий вид информационной схемы технологической линии из двух ступеней для построения математической модели методом передаточных функций
Библиографическая ссылка
Лобасенко Б.А., Котляров Р.В., Сазонова Е.К. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРОЦЕССА МЕМБРАННОГО КОНЦЕНТРИРОВАНИЯ НА ОСНОВЕ КИБЕРНЕТИЧЕСКОГО ПОДХОДА // Фундаментальные исследования. 2016. № 2-1. С. 70-75;URL: https://fundamental-research.ru/ru/article/view?id=39882 (дата обращения: 07.01.2026).
DOI: https://doi.org/10.17513/fr.39882



