МНОГОМАСШТАБНОЕ МОДЕЛИРОВАНИЕ СЕРДЕЧНО-СОСУДИСТОЙ СИСТЕМЫ ДЛЯ ОЦЕНКИ ЦЕРЕБРАЛЬНОГО КРОВООБРАЩЕНИЯ
1
Синдеев С.В.
1
Фролов С.В.
1
1 ФГБОУ ВПО «Тамбовский государственный технический университет»
К настоящему времени причины появления и развития нарушений мозгового кровообращения все еще остаются в полной мере не изученными. При изучении генеза нарушений и при оценке предоперационного состояния больных исследование гемодинамики является основной задачей. Предложен метод многомасштабного математического моделирования сердечно-сосудистой системы, позволяющий объединить модели гемодинамики разной размерности для оценки церебрального кровообращения. Предложенный подход был реализован в виде комплекса программ для оценки предоперационного состояния больных с церебральной аневризмой. Полученные результаты математического моделирования согласуются с гемодинамической теорией генеза церебральных аневризм. Результаты расчета на основе модели могут быть использованы врачом для разработки стратегии и тактики лечения церебральных аневризм в зависимости от индивидуальных особенностей сердечно-сосудистой системы пациента.
церебральное кровообращение
персонализированная медицина
генез аневризмы
1. Фролов С.В., Синдеев С.В., Лищук В.А., Газизо ва Д.Ш., Медведева С.А. Четырехкамерная модель сердечно-сосудистой системы человека // Вопросы современной науки и практики. Университет имени В.И. Вернадского. – 2012. – № 2(40). – С. 51–60.
2. Frolov S.V., Sindeev S.V., Liepsch D., Balasso A. Mathematical modeling of blood flow in basilar artery bifurcation region // Transactions TSTU. – 2014. – № 20(1). – P. 50–58.
3. Frolov S.V., Sindeev S.V., Lischouk V.A., Gazizova D.Sh. Hemodynamics modeling of the cardiovascular system with a pulsating heart // Transactions TSTU. – 2012. – № 18(3). –P. 546–551.
4. Frolov S.V., Sindeev S.V., Lischouk V.A., Gazizo va D.Sh., Liepsch D., Balasso A. Development of multiscale hemodynamics model for research of basilar artery circulation // Problems of Contemporary Science and Practice. Vernadsky University. – 2013. – № 4(48). – P. 46–53.
5. Sindeev S.V., Frolov S.V., Bauer J.S. Mathematical modeling of hemodynamics in patient-specific model of cerebral aneurysm // Transactions TSTU. – 2015. – № 3(21). – P. 424–428.
Исследование гемодинамики является основной задачей при оценке церебрального кровообращения. В работе авторами предлагается концепция многомасштабной математической модели ССС, позволяющей объединить модели гемодинамики разной размерности для оценки церебрального кровообращения. Многомасштабная модель может быть использована для выявления зависимости между возникновением аневризмы и отдельными факторами глобальной гемодинамики и патологиями сердца, разработки рекомендации по лечению церебральных аневризм в зависимости от индивидуальных особенностей ССС пациента.
Разработка многомасштабной модели гемодинамики требует описания ССС набором моделей, отличающихся размерностью и объединенных соответствующими граничными условиями [4]. Предлагается структура многомасштабной модели сердечно-сосудистой системы, представленная на рис. 1.
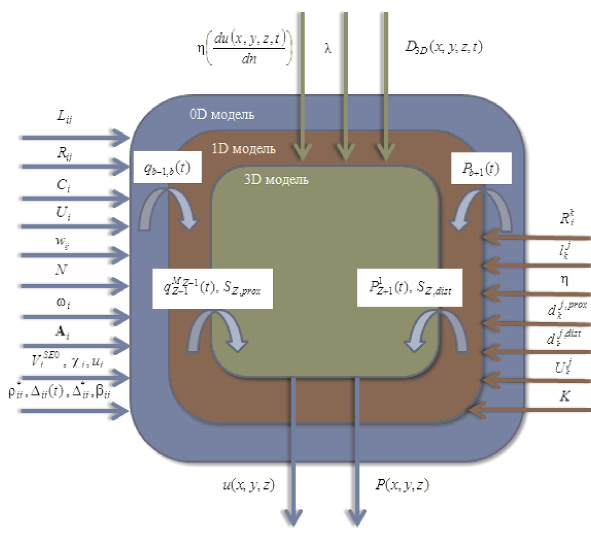
Рис. 1. Схема многомасштабной модели сердечно-сосудистой системы
Входными данными для модели глобальной гемодинамики (0D модель) [1, 3] являются: Lij – инерционность тока крови из i-й камеры в j-ю, (Topp?c2)/cм3; Rij – сопротивление связи, (Topp?c)/cм3; Ci – эластичность i-й камеры, cм3/Topp; Ui – ненапряженный объем i-й камеры, cм3; wij – коэффициент, определяющий связь между камерами ССС; N – количество камер в 0D модели гемодинамики; ?i – объем псевдополости i-го желудочка; Ai – вектор параметров i-го желудочка;  – объем полости желудочка, образованной из элементов постоянной длины, cм3; ?i, ui – константы закона Старлинга;
– объем полости желудочка, образованной из элементов постоянной длины, cм3; ?i, ui – константы закона Старлинга; 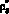 – проводимость открытого клапана, cм3/(Topp?c); ?ij(t) – объем крови, прошедшей через клапан в обратном направлении, cм3;
– проводимость открытого клапана, cм3/(Topp?c); ?ij(t) – объем крови, прошедшей через клапан в обратном направлении, cм3; 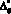 – закрывающий объем, cм3; ?ij – коэффициент, характеризующий скорость снижения проводимости клапана при обратном кровотоке.
– закрывающий объем, cм3; ?ij – коэффициент, характеризующий скорость снижения проводимости клапана при обратном кровотоке.
Вектор параметров i-го желудочка Ai включает
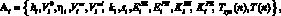
где hi – толщина стенки желудочка, см; 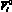 – ненапряженный объем желудочка, cм3; ?i – коэффициент вязкости миокарда, Topp?c;
– ненапряженный объем желудочка, cм3; ?i – коэффициент вязкости миокарда, Topp?c; 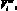
 – ударный и конечный диастолический объем желудочка, cм3; ki – насосный коэффициент желудочка; si – доля сократительных нитей в площади поперечного сечения сердечной мышцы, (0 < s < 1);
– ударный и конечный диастолический объем желудочка, cм3; ki – насосный коэффициент желудочка; si – доля сократительных нитей в площади поперечного сечения сердечной мышцы, (0 < s < 1); 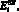


 – параметры аппроксимации для напряжения в стенке камеры; Tsys(n) – время систолы в n-м кардиологическом цикле, c; T(n) – время начала n-го кардиологического цикла (начало систолы), c; n – номер кардиологического цикла.
– параметры аппроксимации для напряжения в стенке камеры; Tsys(n) – время систолы в n-м кардиологическом цикле, c; T(n) – время начала n-го кардиологического цикла (начало систолы), c; n – номер кардиологического цикла.
Выходными данными модели глобальной гемодинамики являются значения объема крови в камере (Vi – объем крови в i-й камере ССС, cм3), давления крови в камере (Pi – давление в i-й камере, Topp) и объемного кровотока между камерами модели сердечно-сосудистой системы (qij – кровоток из i-й камеры в j-ю, cм3/с).
Для модели гемодинамики артериального русла (1D модели) входными данными являются: 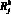 – сопротивление j-го участка k-й артерии, cм3/(Topp?c);
– сопротивление j-го участка k-й артерии, cм3/(Topp?c); 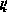 – длина j-го участка k-й артерии, см; ? – коэффициент динамической вязкости крови, Topp?c;
– длина j-го участка k-й артерии, см; ? – коэффициент динамической вязкости крови, Topp?c; 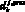 – проксимальный диаметр k-й артерии, см;
– проксимальный диаметр k-й артерии, см; 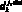 – дистальный диаметр k-й артерии, см;
– дистальный диаметр k-й артерии, см; 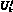 – ненапряженный объем j-го элементарного участка k-й артерии; K – количество артерий в модели гемодинамики артериального русла.
– ненапряженный объем j-го элементарного участка k-й артерии; K – количество артерий в модели гемодинамики артериального русла.
Для корректного использования модели гемодинамики артериального русла граничные условия на входе и выходе из артериальной системы задаются, используя значения, рассчитанные по модели глобальной гемодинамики. В качестве таких условий могут использоваться входной поток в артериальное русло и выходное давление в артериальном русле.
Тогда
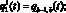
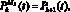 k ? [K – W, K],
k ? [K – W, K],
где 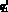 – кровоток первого элементарного участка входной артерии верхней части тела, см3/с; qb–1, b – кровоток из аорты в артерии верхней части тела, см3/с;
– кровоток первого элементарного участка входной артерии верхней части тела, см3/с; qb–1, b – кровоток из аорты в артерии верхней части тела, см3/с; 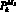 – давление в последнем элементарном участке выходной артерии верхней части тела, Topp; Pb+1 – давление в камере b + 1 0D модели гемодинамики, Topp; W – количество терминальных артерий в модели артериального русла.
– давление в последнем элементарном участке выходной артерии верхней части тела, Topp; Pb+1 – давление в камере b + 1 0D модели гемодинамики, Topp; W – количество терминальных артерий в модели артериального русла.
Выходными данными для модели гемодинамики артериального русла являются: кровоток 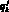 в j-м участке k-й артерии, см3/с; давление
в j-м участке k-й артерии, см3/с; давление 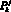 в j-м элементарном участке k-й артерии, Topp; объем крови
в j-м элементарном участке k-й артерии, Topp; объем крови 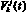 в j-м элементарном участке k-й артерии, см3).
в j-м элементарном участке k-й артерии, см3).
Входными данными для модели локальной гемодинамики церебральной артерии (3D модель) [2,5] являются: 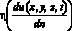 – динамическая вязкость крови в точке (x, y, z) в момент времени t, Topp?c; ? – плотность крови, кг/см3; D3D(x, y, z, t) – расчетная область в момент времени t.
– динамическая вязкость крови в точке (x, y, z) в момент времени t, Topp?c; ? – плотность крови, кг/см3; D3D(x, y, z, t) – расчетная область в момент времени t.
Для корректного расчета модели гемодинамики церебральной артерии требуется задание соответствующих начальных
u(x, y, z, 0) = u0(x, y, z);
P (x, y, z, 0) = P0(x, y, z)
и граничных условий

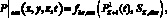
где u0(x, y, z) – скорость крови в церебральной артерии в начальный момент времени, см/с; P0(x, y, z) – давление крови в церебральной артерии в начальный момент времени, Topp; 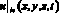 – значение скорости крови на входной границе церебральной артерии, см/с;
– значение скорости крови на входной границе церебральной артерии, см/с; 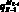 – объемный кровоток начального сегмента церебральной артерии Z, cм3/с; fbc,in – функция преобразования значения объемной скорости на входе церебральной артерии в трехмерный профиль, учитывающий положение артерии; SZ,prox – площадь проксимальной части церебральной артерии, cм2; SZ,dist – площадь дистальной части церебральной артерии, cм2;
– объемный кровоток начального сегмента церебральной артерии Z, cм3/с; fbc,in – функция преобразования значения объемной скорости на входе церебральной артерии в трехмерный профиль, учитывающий положение артерии; SZ,prox – площадь проксимальной части церебральной артерии, cм2; SZ,dist – площадь дистальной части церебральной артерии, cм2; 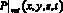 – значение давления на выходной границе церебральной артерии, Topp; fbc,out – функция преобразования значения выходного давления из модели гемодинамики артерий верхней части тела;
– значение давления на выходной границе церебральной артерии, Topp; fbc,out – функция преобразования значения выходного давления из модели гемодинамики артерий верхней части тела; 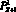 – значение выходного давления церебральной артерии, полученное из 1D модели гемодинамики, Topp.
– значение выходного давления церебральной артерии, полученное из 1D модели гемодинамики, Topp.
Выходными данными модели локальной гемодинамики церебральной артерии являются значения скорости крови u(x, y, z) и давления P(x, y, z), изменяющиеся по трем пространственным координатам в области D3D(x, y, z, t).
Таким образом, описан подход к многомасштабному моделированию ССС, позволяющий объединить модель глобальной гемодинамики (0D модель), модель гемодинамики артериального русла (1D модель) и модель локальной гемодинамики церебральной артерии (3D модель).
Предложенный подход был реализован в виде комплекса программ для оценки церебральной гемодинамики. Схема взаимодействия модулей комплекса представлена на рис. 2. При расчете 0D модели происходит определение граничных условий для модели гемодинамики артериального русла (1D модель). После того как расчет 0D модели гемодинамики завершен, происходит расчет модели гемодинамики артериального русла. Так как расчет модели гемодинамики артериального русла обладает значительной вычислительной сложностью, то был предложен метод параллельного расчета данной модели с использованием технологии GPGPU (реализация NVIDIA CUDA). На данном этапе также определяются граничные условия для 3D модели гемодинамики. Наибольшей вычислительной сложностью обладает 3D модель локальной гемодинамики церебральной артерии, для расчета которой были использованы параллельные вычисления на кластере «Ломоносов» МГУ им. М.В. Ломоносова с применением технологии MPI. После завершения расчета модели локальной гемодинамики церебральной артерии осуществляется переход на следующий временной шаг моделирования и процесс вычисления повторяется.
В качестве примера был выбран пациент с терминальной аневризмой базилярной артерии. Была произведена процедура идентификации разработанных моделей гемодинамики. На рис. 3 представлены сегментированные данные участка церебральных артерий, полученных с помощью КТ-ангиографии, и выделенный для расчета участок базилярной артерии.
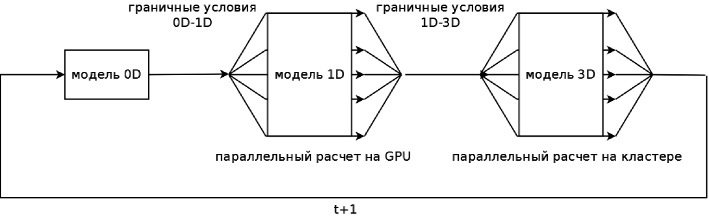
Рис. 2. Схема обмена данными между модулями программного комплекса оценки церебральной гемодинамики
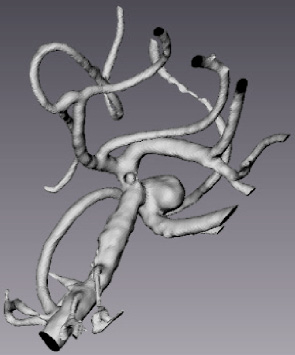
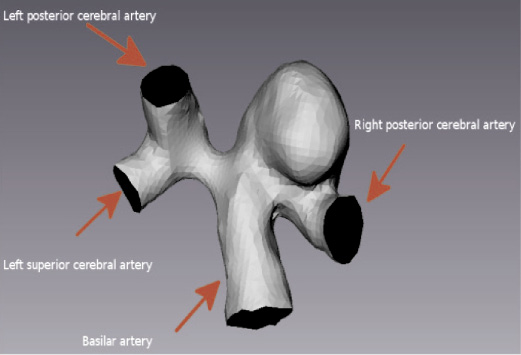
а б
Рис. 3. Сегментированные данные КТ-ангиографии пациента с аневризмой базилярной артерии: а – участок церебральных артерий; б – выделенная область с аневризмой базилярной артерии
Был произведен расчет гемодинамики в индивидуальной модели аневризмы базилярной артерии. На рис. 4 представлены линии тока в момент систолического пика Tsys = 0,2 с. Наибольшую скорость поток имеет во входном сегменте бифуркации левой церебральной артерии – 1,14 м/с, что в два раза превосходит среднюю по сечению скорость во входном сегменте базилярной артерии. В полости аневризмы наблюдается нестабильный вихрь, который может служить причиной образования тромбов внутри аневризмы и дальнейшей блокировки тока крови в церебральные артерии. Минимальная скорость тока крови наблюдается в полости аневризмы, где в отдельных областях скорость снижается до 8,94?10–7 м/с и в целом не превосходит 0,5 м/с, что составляет около 65 % от осевой скорости крови во входном сегменте базилярной артерии.
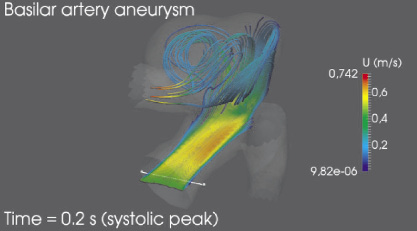
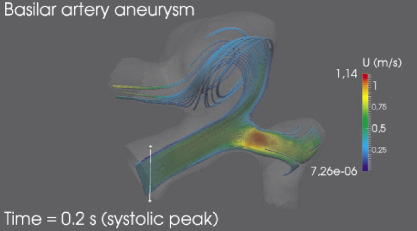
Рис. 4. Линии тока для индивидуализированной модели аневризмы базилярной артерии
Для детального анализа гемодинамики внутри аневризмы была выбрана секущая плоскость, расположенная в центре аневризмы. Анализ распределения скорости показал, что в центральной части секущей плоскости наблюдается область с низким значением модуля скорости, который изменяется в диапазоне [1?10–4; 0,15] м/с. Данный факт обусловлен наличием вихря в центральной области аневризмы, благодаря которому значительный объем крови движется в противоположном естественному току крови направлении. В то же время область максимальных скоростей потока крови смещена к куполу аневризмы. В данной области скорость крови изменяется в диапазоне [0,25; 0,482] м/с. При этом средний модуль скорости в секущей плоскости в момент систолического пика равен 0,19 м/с.
Приведенное на рис. 5 распределение пристеночного напряжения сдвига показывает, что большая часть поверхности купола аневризмы находится под воздействием пристеночного напряжения сдвига в диапазоне [0,2; 2] Па, что является критическим значением, обуславливающим дальнейшее изменение внутреннего слоя стенки полости аневризмы и разрушение клеток эндотелия. Помимо этого значительную опасность дальнейшего развития заболевания представляет собой начальный сегмент бифуркации левой мозговой артерии в области, где пристеночное напряжение сдвига достигает максимального значения более 40 Па, что также может привести к разрушению внутреннего слоя стенки церебральной артерии.
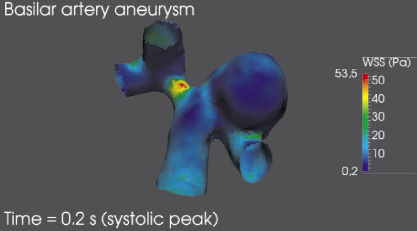
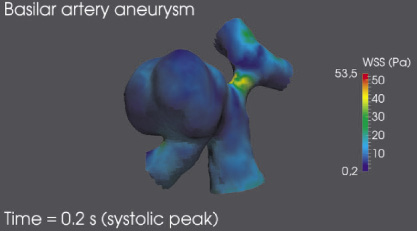
Рис. 5. Пристеночное напряжение сдвига в момент систолического пика
Полученные результаты математического моделирования согласуются с гемодинамической теорией генеза церебральных аневризм. Предложенный метод и комплекс программ многомасштабного моделирования гемодинамики ССС с использованием высокопроизводительных вычислений может быть использован на предоперационном этапе для индивидуальной оценки состояния церебральной гемодинамики пациента. На основании анализа полученных результатов врачом может быть принято решение о выборе стратегии и тактики лечения.
Синдеев С.В., Фролов С.В. МНОГОМАСШТАБНОЕ МОДЕЛИРОВАНИЕ СЕРДЕЧНО-СОСУДИСТОЙ СИСТЕМЫ ДЛЯ ОЦЕНКИ ЦЕРЕБРАЛЬНОГО КРОВООБРАЩЕНИЯ // Фундаментальные исследования. – 2015. – № 12-5.
– С. 950-954;
URL: https://fundamental-research.ru/ru/article/view?id=39657 (дата обращения: 27.04.2024).











