Для современной науки большой интерес представляют процессы полимеризации, так как их исследование дает возможность изучить свойства и характеристики получаемого полимерного продукта, а затем осуществить синтез полимеров c заданными свойствами на базе ограниченного числа основных промышленных мономеров. Распространенным примером полимерных продуктов являются синтетические каучуки. Они представляют собой синтетические полимеры, способные перерабатываться в резину путем вулканизации. Одними из наиболее востребованных видов синтетических каучуков продолжают оставаться бутадиен-стирольные каучуки эмульсионной полимеризации. В связи с этим исследования процесса сополимеризации бутадиена со стиролом по радикально-цепному механизму до сих пор не теряют своей актуальности. Эта область дает наилучшие возможности для изучения статистических особенностей и факторов, влияющих на них, и позволяет с высокой точностью описывать протекание процесса [7].
Материалы и методы исследования
Ранее в работе [4] был рассмотрен алгоритм моделирования процесса сополимеризации бутадиена со стиролом в реакторе, основанный на методе Монте-Карло. Но он применим лишь для периодического процесса, а производство бутадиен-стирольного каучука осуществляется в батарее последовательно соединенных между собой полимеризаторов при температуре 5–10 °C. В данной работе будем рассматривать модификацию алгоритма моделирования с учетом проведения процесса в каскаде реакторов.
Для непрерывного процесса теряет смысл само понятие времени реакции; можно говорить лишь о некотором среднем времени пребывания как о случайной величине, которая характеризуется вероятностной функцией распределения. Но при этом возможно, что молекулярно-массовое распределение полимера будет искажаться, так как на случайное молекулярно-массовое распределение продукта накладывается случайное распределение времени пребывания частиц в системе [5].
Согласно [8], вероятность того, что частица проводит время от t до t + dt в текущем реакторе, равна p(t)dt, но так как рассматриваемые полимеризаторы представляют собой реакторы идеального смешения непрерывного действия, то для них величина p(t) рассчитывается по формуле
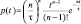 , (1)
, (1)
где n – количество реакторов в системе; τ – среднее время пребывания реакционной смеси в одном реакторе (ч).
Следовательно, для модификации алгоритма моделирования на случай каскада реакторов каждую частицу системы необходимо охарактеризовать двумя дополнительными параметрами: номер реактора, в котором она находится, и время ее пребывания в текущем реакторе. Для расчета времени пребывания на отрезке от 0 до 5 ч генерируется равномерно распределенное случайное число r, на основе которого согласно распределению (1) рассчитывается время пребывания частицы в зависимости от того, в какую часть отрезка попадет число r. Отрезок от 0 до 5 ч был выбран в связи с тем, что сумма вероятностей различных времен пребывания с шагом 0,1 на данном отрезке равна 1, то есть данные события образуют полную группу.
После этого следует вычислить шаг времени между текущей и предыдущей реакциями (c) [6]:
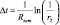 (2)
(2)
При этом общее время протекания процесса рассчитывается согласно формуле t = t + Δt, и в каждый момент времени необходимо оценивать вероятность осуществления перехода частицы системы в следующий реактор: если ее время пребывания в текущем реакторе истекло, то необходимо перевести ее в следующий реактор и рассчитать новое время пребывания.
Результаты исследования и их обсуждение
На основе вышеописанной модели разработан программный комплекс в среде программирования Visual Studio на языке C# [2, 3]. Он позволяет проводить расчет процесса свободнорадикальной сополимеризации бутадиена со стиролом в батарее последовательно соединенных полимеризаторов на основе математической модели. При проведении вычислительного эксперимента исследован процесс сополимеризации бутадиена со стиролом со следующей рецептурой:
● рабочий объем полимеризатора V = 10,8 м3;
● число полимеризаторов: 12;
● объемная скорость потока Cf = 9,5982 м3/ч;
● время нахождения реакционной смеси в одном полимеризаторе θ = V/Cf = 1,125 ч;
● нагрузка на батарею по мономерам: 3,0 т/ч (бутадиен 70 %, стирол – 30 %);
● дозировка инициатора (гидроперекись пинана): 0,048 масс.ч.;
● дозировка регулятора (трет-додецил меркаптан): 0,28 масс.ч.;
● соотношение вода/мономеры = 220,8/100.
При этом было учтено, что процесс является непрерывным, и каждый час происходит добавление новой порции реакционной смеси.
Так как в любом образце полимера присутствуют макромолекулы разных размеров, то для оценки качества получаемого продукта принципиально важное значение составляет картина молекулярно-массового распределения [1], демонстрирующая соотношение количеств макромолекул различной молекулярной массы. Так как ключевым моментом модели является имитация роста каждой макромолекулы, то для построения молекулярно-массового распределения достаточно произвести фракционирование полученного к данному моменту времени сополимера по массе макромолекул и на основе статистических данных построить зависимость между молекулярной массой и массовой долей фракций полимера для текущей конверсии мономеров [4].
На рис. 1–3 представлены кривые молекулярно-массового распределения продукта сополимеризации бутадиена со стиролом в разные моменты времени проведения процесса.
Анализируя молекулярно-массовое распределение, можно отметить, что со временем молекулярно-массовое распределение продукта сополимеризации принимает более устоявшийся характер и повторяет поведение модельного распределения Шульца – Флори, которое учитывает обрыв цепи в результате взаимодействия с регулятором. Также в сополимере наблюдается преобладание фракции с молекулярной массой около 5∙104–6∙104, а пик кривой соответствует значению среднечисленной молекулярной массы сополимера при текущей конверсии мономеров.
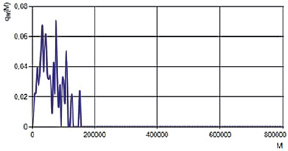
Рис. 1. Молекулярно-массовое распределение сополимера при t = 2 ч
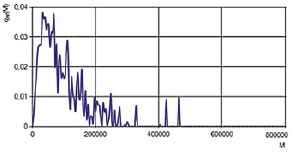
Рис. 2. Молекулярно-массовое распределение сополимера при t = 27 ч
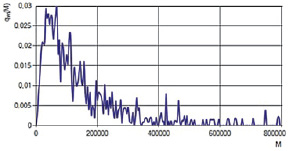
Рис. 3. Молекулярно-массовое распределение сополимера при t = 54 ч
Выводы
Таким образом, предложенный алгоритм моделирования адекватно описывает процесс сополимеризации бутадиена со стиролом. Для осуществления моделирования процесса в батарее последовательно соединенных полимеризаторов учтено распределение по времени пребывания частиц системы. Так как в основе данного подхода лежит имитация роста каждой макромолекулы и отслеживание процессов, происходящих с ней, то он позволяет накапливать информацию о составе и длине образующихся цепей сополимера и в дальнейшем исследовать процесс в динамике. Получаемая информация дает возможность исследовать характеристики продукта сополимеризации в любой момент времени и проводить расчет молекулярно-массового распределения.
Рецензенты:
Муравьева Е.А., д.т.н., профессор, филиал, ФГБОУ ВПО «Уфимский государственный нефтяной технический университет», г. Стерлитамак;
Галиев А.Л., д.т.н., профессор, филиал, ФГБОУ ВПО «Уфимский государственный авиационный технический университет», г. Стерлитамак.
Библиографическая ссылка
Михайлова Т.А., Григорьев И.В., Мустафина С.А. ИССЛЕДОВАНИЕ СИНТЕЗА БУТАДИЕН-СТИРОЛЬНОГО СОПОЛИМЕРА НА ОСНОВЕ МЕТОДА МОНТЕ-КАРЛО С УЧЕТОМ РАСПРЕДЕЛЕНИЯ ПО ВРЕМЕНИ ПРЕБЫВАНИЯ // Фундаментальные исследования. 2015. № 5-3. С. 517-520;URL: https://fundamental-research.ru/ru/article/view?id=38292 (дата обращения: 13.01.2026).



