Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Кобрунов А.И. 1 Кожевникова П.В. 1

---

1 ФГБОУ ВПО «Ухтинский государственный технический университет»

Рассмотрена задача прогнозирования параметров физико-геологической модели среды для неоднородных сред на основе синтеза принципов нечеткого вывода и моделей рассеяния. Неоднородность среды рассматривается как изучаемое свойство, информация о котором регистрируется в форме рассеяния параметров, по которым реализуется прогноз моделей. Описан выбор и обоснование функции принадлежности при прогнозировании параметров геологических сред в условиях неопределенности. Прогнозирование параметров заменено прогнозированием их полей рассеяния. Рассмотрены два метода аппроксимации функции принадлежности. Проведен сравнительный анализ использования каждого метода. Первый метод основан на введении принципа максимальной энтропии для элемента аппроксимации. В качестве такой функции был выбран нормальный закон распределения. Второй метод основан на использовании принципа равномерного рассеяния информации о значении параметра по мере удаления от значения в фазовом пространстве.

Статья в формате PDF

1067 KB

поле рассеяния

функция принадлежности

прогноз параметров

петрофизические зависимости

1. Aхмед Оуенес. Практическое применение нечеткой логики и нейронных сетей для трещинных коллекторов // Компьютеры и науки о Земле, т. 26, вып. 8, 1 октября 2000. – С. 953–962.

2. Вендельштейн Б.Ю., Резванов Р.А. Геофизические методы определения параметров нефтегазовых коллекторов: при подсчете запасов и проектировании разработки месторождений. – М.: Недра, 1978. – 318 с.

3. Жирабок А.Н. Нечеткие множества и их использование для принятия решений // Соросовский образовательный журнал. – 2001. – Т. 7. – № 2. – С. 109–115.

4. Задэ Л.A. Нечеткие множества // Информация и контроль. – 1965. – Вып. 8, № 3. – С. 338–353.

5. Мамдани Е.Х. Применение нечетких алгоритмов для управления простыми динамическими объектами. Инженеры-электрики, материалы IEE. – 1974. – № 121(12). – С. 1585–1588.

6. Парк С.У., Бера A.К. Максимальная энтропия авторегрессионной условной гетероскедастичности модели // журнал эконометрики. – 2009. – Т. 150. – № 2. – С. 219–230.

7. Тани Т., Сакода М., Танака К. Нечеткое моделирование по ID3-алгоритм и его применение для прогнозирования температуры на выходе нагревателя // Нечеткие системы: материалы Международной конференции IEEE. – 1992. – С. 923–930.

В N-мерном пространстве S параметров s = {s₁, s₂, s₃, ..., s_i; i = 1...N} экспериментально измерены значения s^j ∈ S, j = 1...M, образующие в нем подмножество A ⊂ S. Данные A ⊂ S являются экспериментальным основанием для формирования экспертного правила прогноза одних параметров η из числа s_i, i = 1...N, по измеренным другим, обозначаемым ξ: s = ξ×η. Традиционно таким экспертным правилом в задачах промысловой геофизики служат петрофизические зависимости [2], представляющие данные A в форме регрессионных зависимостей одних параметров от других. Такой способ достаточно конструктивен и широко применяется в настоящее время, тем не менее он не учитывает реальные свойства неоднородностей в изучаемых параметрах.

Согласованное с обучающими данными A ⊂ S экспертное правило 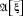вывода заключения о прогнозируемых параметрах 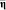из информации об измеренных 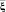реализуется: определением нечеткого отношения μA(ξ, η) = μA(s) по обучающей выборке A [4] между параметрами η и ξ; представлением конкретных измерений 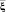в форме нечеткой величины и последующим использованием алгоритма нечеткого логического вывода [5] о величине η.

Нечеткое моделирование широко применяется в нефтегазовой промышленности. К примеру, использование алгоритма ID3 в области машинного обучения, который был применен для выбора эффективных параметров в рамках нечеткой модели и вычислениях их граничных значений [7], а также использование нового подхода к трещинно-пластовым характеристикам, который основан на средствах искусственного интеллекта [1].

Для представления данных A в форме нечетких отношений, а измеренных значений параметра 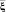, по которым выполняется прогноз, в форме нечетких величин основанием является понятие поле рассеяния.

Полем рассеяния для данных s^j ∈ S, j = 1...M назовем функцию A^ε(s) в фазовом пространстве, такую, что для каждой подобласти ΔS из разбиения S

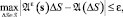(1)

где A(ΔS) – число значений из A ⊂ S, целиком лежащее в ΔS.

Функция принадлежности μA(s) для измеренных значений параметров s ∈ S как нечетких величин есть нормированное к единице поле рассеяния A^ε(s):

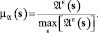(2)

Для построения поля рассеяния A^ε(s) пространство S покрывается сеткой ΔSk, k = 1...K таким образом, чтобы была покрыта вся область значений параметров из A, 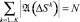и ставится задача поиска функции рассеяния по (1):

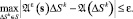(3)

Выбирается K(h, s) – базисная система функций, параметризованная вектором параметров h, и ставится задача нахождения A^ε(s) в виде

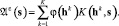(4)

В данном случае φ(h^k), требующая нахождения из (4), функция. Соотношение (4) означает, что поле рассеяния ищется в форме линейной комбинации базовых функций K(h, s), свойства которых определяют принцип для аппроксимации поля рассеяния A^ε(s) и функции принадлежности μ_A(s).

1 метод

В качестве традиционных приемов аппроксимации функции принадлежности используют треугольные трапециевидные и другие априори вводимые зависимости [3]. В отличие от данных приемов для элемента аппроксимации K(h, s) введем принцип максимальной энтропии. В соответствии с этим принципом в качестве элемента аппроксимации была выбрана функция нормального закона распределения [6], в качестве параметра h, в котором служит математическое ожидание:

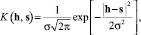(5)

где σ² – второй центральный момент – дисперсия нормального распределения.

Тогда из (4) получаем

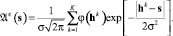(6)

Соотношение (6) интерпретируется как диффузионное рассеяние в бесконечном однородном пространстве параметров точечных источников, расположенных в h^k.

2 метод

При этом с аппроксимацией поля рассеяния A^ε(s) с помощью функций K(h, s), связанных с фундаментальным решением уравнения диффузии как распределением, имеющим максимум меры неопределенности, могут быть введены и иные аппроксимирующие поля рассеяния функции, также имеющие физическое осмысление конструирования. Например, для выбора K(h, s), являющегося аппроксимирующим элементом поля рассеяния A^ε(s), можно воспользоваться принципом равномерного рассеяния информации о значении s^j параметра s по мере удаления от значения sj в фазовом пространстве S. Это приводит к обратной пропорциональности K(h, s) от :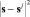

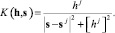(7)

Такой вид аппроксимации предполагает равное распределение информации о s^j вдоль окружности радиуса 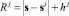. По мере удаления от точки s^j информация об этом значении распределяется на все большие и большие окружности. В итоге приходим к уравнению

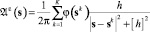. (8)

По приведенным методам расчета аппроксимации функции принадлежности, принимая в качестве функции поля рассеяния A^ε(s) соотношения (6) и (8), проведем вычислительные эксперименты.

Проведенные эксперименты

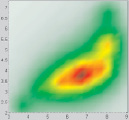
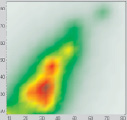
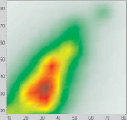
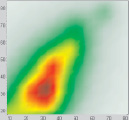
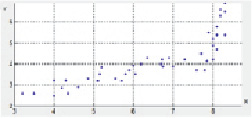
1 эксперимент. Пусть в результате измерений получено отношение между петрофизическими характеристиками, представленное на рис. 1, а.

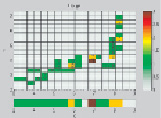
а б

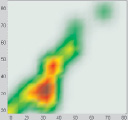
Рис. 1. а – отношение между петрофизическими характеристиками; б – карта плотности данных

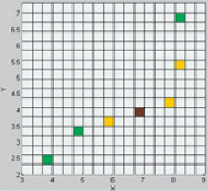
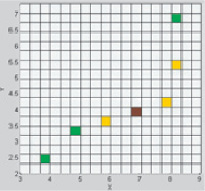
а б

Рис. 2. а – карта точечных источников с параметром ζ = 0,6; б – карта точечных источников с параметром h = 0,6

На основе отношения петрофизических характеристик была получена карта плотности данных (рис. 1, б), отображающая, сколько данных попало в каждую ячейку сетки.

Затем для каждого метода получена карта точечных источников с минимальным числом источников, удовлетворяющим условию 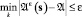. В конкретном примере это число оказалось равным 7 (перебиралось от 7 до 25). Значения в источниках были найдены посредством решения системы линейных уравнений из (6) и (8). Результат представлен на рис. 2, а и б соответственно.

Как видно из рис. 2, карты точечных источников, полученные разными методами, совпадают.

На основании данных карт были рассчитаны поля рассеяния. Ниже приведены примеры с различными параметрами при построении полей рассеяния (табл. 1, 2).

2 эксперимент

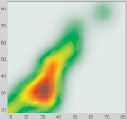
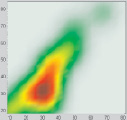
Пусть в результате измерений получено отношение между петрофизическими характеристиками, представленное на рис. 3, а. Аналогично эксперименту 1 была построена карта плотности данных (рис. 3, б). Затем была получена карта 9-ти точечных источников ( рис. 3, в).

На основании карты источников были рассчитаны поля рассеяния. Ниже приведены примеры с различными параметрами при построении полей рассеяния (табл. 3, 4).

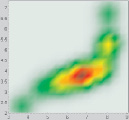
Таблица 1

Поля рассеяния, полученные с помощью первого метода

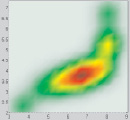
Таблица 2

Поля рассеяния, полученные с помощью второго метода

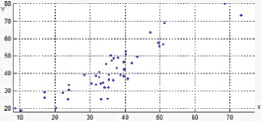
а

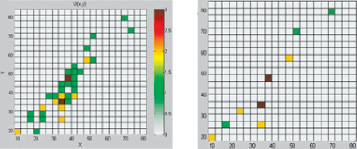
б в

Рис. 3. а – отношение между петрофизическими характеристиками; б – карта плотности данных; в – карта точечных источников (9 источников)

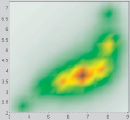
Таблица 3

Поля рассеяния, полученные с помощью первого метода

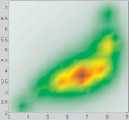
Таблица 4

Поля рассеяния, полученные с помощью второго метода

Вывод

Проведенные эксперименты демонстрируют достаточно высокую эффективность аппроксимации разброса данных функции правдоподобия в форме нормального закона распределения и уравнений диффузии. Различие свойств аппроксимации не значительно. Следует рекомендовать для формирования правила логического вывода соотношение в форме, основанной на фундаментальных уравнениях диффузии, как наиболее содержательной в физическом смысле.

Рецензенты:

Некучаев В.О., д.ф.-м.н., профессор, заведующий кафедрой физики, ФГБОУ ВПО УГТУ, г. Ухта;

Яковлев С.А., д.т.н., профессор, Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина), г. Санкт-Петербург.

Библиографическая ссылка