На сегодняшний день энергосбережение является одним из основных приоритетов энергетической стратегии Российской Федерации согласно № 261-ФЗ «Об энергосбережении и о повышении энергетической эффективности и о внесении изменений в отдельные законодательные акты Российской Федерации» [11] и № 190-ФЗ «О теплоснабжении» [12]. Анализ результатов современных исследований фактических теплопотерь трубопроводов тепловых сетей [14] выявил существенные превышения по сравнению с нормативными данными [8]. Теплопередача в случае теплопровода, находящегося в полуограниченном массиве грунта, является очень сложным процессом. На поток теплоты от трубопровода накладывается естественный тепловой поток со стороны грунта, частично «замещающий» теплопотери теплопровода [13]. Когда две трубы тепловой сети проложены бесканально в грунте, в результате возникновения тепловых потерь вокруг теплопроводов, образуются и температурные поля, воздействующие друг на друга и способствующие сокращению тепловых потерь каждой трубы в отдельности. Соседний теплопровод может равноценно увеличить сопротивление для рассматриваемого трубопровода [3]. Следовательно, очень важно найти методы, позволяющие определить действительное значение теплопотерь, целью которых является корректировка нормативных величин теплопотерь, предложенных в нормативных документах, например таких, как СНиП 41-03-2003 «Тепловая изоляция оборудования и трубопроводов» [9] и СНиП 41-03-2003 «Тепловая изоляция оборудования и трубопроводов. Актуализированная редакция» [10].
Тепловые потери – это показатели энергоэффективной эксплуатации системы теплоснабжения, так как они играют значительную роль в тарифах на тепловую энергию. Следовательно, определение фактического значения величины теплопотерь является одной из главных практических задач в системе энергоресурсосбережения. Тепловые потери трубопроводов тепловых сетей зависят от различных факторов, таких как диаметр трубопроводов, протяженность, теплоизоляционные материалы, состояния трубопроводов.
Исходя из вышеперечисленного, вопрос нахождения минимальных тепловых потерь остается открытым. Для анализа тепловых потерь трубопроводов тепловой сети предлагается использовать численное моделирование. Современные вычислительные программы позволяют учесть различные факторы, влияющие на величину тепловых потерь. Для повышения эффективности использования тепловой энергии необходимо совершенствовать методы тепловых расчетов систем теплоснабжения.
В данной работе используются следующие методы исследования:
– разработка математической модели теплообмена тепловой сети и окружающей среды;
– применение численных методов решения основных задач теплового расчета;
– изучение тепловых полей и потоков для различных сечений теплопроводов тепловых сетей.
Расчёт температур Т, К, в трубопроводах выполняется с помощью закона Фурье для нестационарного температурного поля [7]:
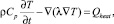 (1)
(1)
где r – плотность, кг/м3; t – время, с; Ср = Ср(Т) – изобарная теплоёмкость воздуха, Дж/(кг∙К); λ = λ(Т) – коэффициент теплопроводности, Вт/(м∙К); Qheat – источник или сток теплоты, Вт/м3.
Для задания начальных условий будем считать, что процесс теплопередачи исследуется с момента времени t = 0 с. Постановка задачи принята стационарная. В этом случае для её решения строится нестационарный процесс, решение которого с течением времени (фиктивного) оказывается независимым от него и приводится к решению исходной стационарной задачи.
При расчётах начальным значением температуры T (t = 0) принимаем:
– температура воды T (t = 0) = 338,15 К для прямого трубопровода и T (t = 0) = 323,15 К для обратного трубопровода;
– температура грунта T (t = 0) = 279,15 К.
Влияние источника (горячей воды в трубах) учитывается с помощью граничного условия:
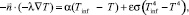 (2)
(2)
где  – нормальный единичный вектор к граничной поверхности, направленный наружу от граничной области; λ – коэффициент теплопроводности, Вт/(м∙К); Т – температура, К; Тinf – температура окружающей среды, К; ε – степень черноты поверхности; σ = 5,6704·10–8 Дж·с–1·м–2·К–4 – константа Стефана – Больцмана; α – коэффициент конвективного теплообмена, Вт/(м2∙К): от воды к внутренним стенкам трубопровода принимается α = 2500 Вт/(м2∙К) [5].
– нормальный единичный вектор к граничной поверхности, направленный наружу от граничной области; λ – коэффициент теплопроводности, Вт/(м∙К); Т – температура, К; Тinf – температура окружающей среды, К; ε – степень черноты поверхности; σ = 5,6704·10–8 Дж·с–1·м–2·К–4 – константа Стефана – Больцмана; α – коэффициент конвективного теплообмена, Вт/(м2∙К): от воды к внутренним стенкам трубопровода принимается α = 2500 Вт/(м2∙К) [5].
Средняя температура за зимний период на нижней границе расчётной области – грунта (супеси) на глубине 3,5 м на территории Санкт-Петербурга принята 6 °С [6].
На боковых границах задаётся граничное условие «симметрия»:
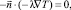 (3)
(3)
где  – нормальный единичный вектор к граничной поверхности, направленный наружу от граничной области; λ – коэффициент теплопроводности, Вт/(м∙К); Т – температура, К.
– нормальный единичный вектор к граничной поверхности, направленный наружу от граничной области; λ – коэффициент теплопроводности, Вт/(м∙К); Т – температура, К.
Численное решение уравнения (1) для трубопроводов с тепловой изоляцией из пенополиуретана с системой оперативного дистанционного контроля влажности (ППУ с ОДК) для бесканальной подземной прокладки выполнено методом конечных элементов в программе «Comsol Multiphysics» 3.5a. Результаты решения приведены на рис. 1 и 2.
На остальных границах задаётся граничное условие «конвективный поток»:
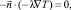 (4)
(4)
где  – нормальный единичный вектор к граничной поверхности, направленный наружу от граничной области; λ – коэффициент теплопроводности, Вт/(м∙К); Т – температура, К.
– нормальный единичный вектор к граничной поверхности, направленный наружу от граничной области; λ – коэффициент теплопроводности, Вт/(м∙К); Т – температура, К.
В воздушных прослойках возникает конвекция, характерная для замкнутых областей. Для расчёта поля скоростей 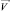 используется система уравнений Навье – Стокса для сжимаемой вязкой жидкости и газа [4]:
используется система уравнений Навье – Стокса для сжимаемой вязкой жидкости и газа [4]:
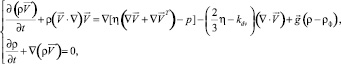 (5)
(5)
где h = h(T) – динамическая вязкость, Па·с.; kdv – объемная («вторая») вязкость, Па·с.; r – плотность, кг/м3; t – время, с; rф – фоновая плотность воздуха, кг/м3; p – динамическое давление воздуха, Па; 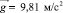 – ускорение свободного падения.
– ускорение свободного падения.
Плотность воздуха рассчитывается с помощью уравнения состояния идеального газа:
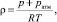 (6)
(6)
где p – динамическое давление воздуха, Па; pатм = 101325 Па – нормальное атмосферное давление; R = 287 Дж/(кг×К) – газовая постоянная воздуха; Т – температура, К.
Начальные условия для скорости и давления следующие:
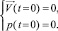 (7)
(7)
На непроницаемых поверхностях для скорости задаётся граничное условие «прилипания»:
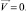 (8)
(8)
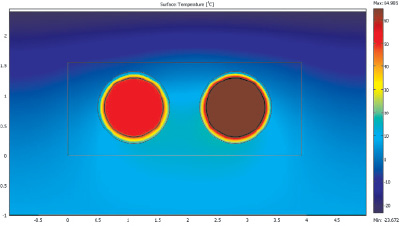
Рис. 1. Поле температур, ºС, теплопроводов двухтрубной тепловой сети условным диаметром 1000 мм с ППУ с ОДК для бесканальной подземной прокладки
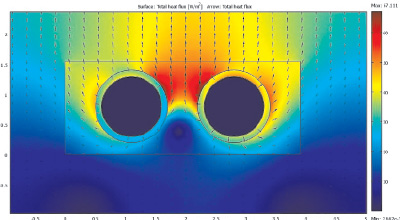
Рис. 2. Тепловой поток, Вт/м2, теплопроводов двухтрубной тепловой сети условным диаметром 1000 мм с ППУ с ОДК для бесканальной подземной прокладки
Для расчёта конвективного и радиационного теплообмена в замкнутых воздушных прослойках со сложной геометрией (с переменными толщинами и пространственными ориентациями) некорректно применять термическое сопротивление, используя соответствующие методики из СНиП 41-03-2003 «Тепловая изоляция оборудования и трубопроводов» [9].
При расчетах радиационного теплообмена воздуха в замкнутых воздушных прослойках используется метод сальдо [2]:
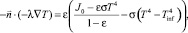 (9)
(9)
где  – нормальный единичный вектор к граничной поверхности, направленный наружу от граничной области; λ – коэффициент теплопроводности, Вт/(м∙К); Т – температура, К; ε – степень черноты поверхности; J0 – удельное теплоизлучение поверхностью тела, Вт/м2; σ = 5,6704·10–8 Дж·с–1·м–2·К–4 – константа Стефана – Больцмана; Тinf – температура окружающей среды.
– нормальный единичный вектор к граничной поверхности, направленный наружу от граничной области; λ – коэффициент теплопроводности, Вт/(м∙К); Т – температура, К; ε – степень черноты поверхности; J0 – удельное теплоизлучение поверхностью тела, Вт/м2; σ = 5,6704·10–8 Дж·с–1·м–2·К–4 – константа Стефана – Больцмана; Тinf – температура окружающей среды.
При расчётах конвективного теплообмена фоновая плотность воздуха rф определяется по уравнению состояния идеального газа, причём температура принимается средняя по слою прослойки.
На рис. 3 и 4 приведены результаты расчёта теплопроводов двухтрубной тепловой сети условным диаметром 125 мм с ППУ с ОДК для подземной прокладки в непроходных каналах типа КН-II.
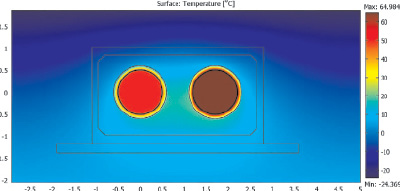
Рис. 3. Поле температур, ºС, теплопроводов двухтрубной тепловой сети условным диаметром 125 мм с ППУ с ОДК для подземной прокладки в непроходных каналах типа КН-II
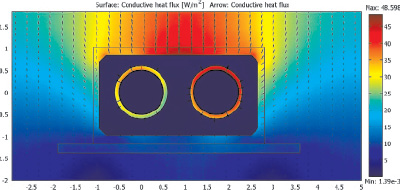
Рис. 4. Тепловой поток за счёт теплопроводности, Вт/м2, теплопроводов двухтрубной тепловой сети условным диаметром 125 мм с ППУ с ОДК для подземной прокладки в непроходных каналах типа КН-II
Численное моделирование тепловых процессов трубопроводов тепловых сетей является актуальной задачей при разработке энергосберегающих мероприятий для системы теплоснабжения. Использование математического моделирования позволяет достаточно эффективно решать сложные научно-технические задачи, не применяя значительных временных и материальных ресурсов. Разработав математическую модель процессов, связанных с двухтрубными теплопроводами, включающую дифференциальные уравнения, а также начальные и граничные условия, можно решить задачу и получить распределение температур и тепловых потоков и сделать их визуализацию. В статье рассматривалась широко распространенная подземная прокладка тепловых сетей, т.к. ГОСТ 30732-2006 [1] и ЕN 253 [15] рекомендуют к широкому внедрению подземную прокладку теплопроводов, в частности бесканальную с тепловой изоляцией из пенополиуретана с системой оперативного дистанционного контроля влажности [1, 15]. Для данного типа прокладки в дальнейшем возможно будет откорректировать значение тепловых потерь. Изучив рисунки, представленные в статье, можно обосновать величины теплопотерь, а именно, чем больше диаметр трубопровода, тем ниже должен быть тепловой поток через стенку теплопровода. Задачи теплопроводности, возникающие в системах теплоснабжения, нечасто имеют решение с помощью аналитического метода. Следствием этого может быть трудность создания математических моделей, сильно зависящих от теплофизических свойств и коэффициентов в граничных условиях, а также сложная геометрия объектов, таких как цилиндры. Таким образом, численные методы, использующие компьютерную реализацию, являются универсальным способом решения задач в системах двухтрубных тепловых сетей.
Рецензенты:
Уляшева В.М., д.т.н., доцент, профессор кафедры теплогазоснабжения и вентиляции, ФГБОУ ВПО «Санкт-Петербургский архитектурно-строительный университет», г. Санкт-Петербург;
Гримитлин А.М., д.т.н., профессор кафедры теплогазоснабжения и вентиляции, ФГБОУ ВПО «Санкт-Петербургский архитектурно-строительный университет», директор некоммерческого партнёрства энергоаудиторов «Инженерные системы аудит» (СПб), президент АВОК Северо-Запад, генеральный директор НПП «ЭКОЮРУС-ВЕНТО», г. Санкт-Петербург.
Библиографическая ссылка
Тарасевич Е.И. ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ТЕПЛООБМЕНА ДЛЯ ДВУХТРУБНЫХ ТЕПЛОВЫХ СЕТЕЙ ПРИ ПОДЗЕМНОЙ КАНАЛЬНОЙ И БЕСКАНАЛЬНОЙ ПРОКЛАДКЕ // Фундаментальные исследования. 2015. № 2-22. С. 4880-4885;URL: https://fundamental-research.ru/ru/article/view?id=38124 (дата обращения: 01.07.2025).



