В работах автора [1, 2, 3] приведены результаты исследований по повышению надежности каналов телемеханики за счет адаптации управляющих сигналов к характеристикам канала, прежде всего к помехам.
В классической литературе по теории информации, например в [5], показано, что для извлечения максимального количества информации из сигнала на входе приемника (сигнал + помеха) необходимо полезный сигнал формировать таким, чтобы его закон распределения дополнял закон распределения помехи до нормального (гауссового) распределения.
Пусть сигнал х0(t) имеет закон распределения р0(x). Этот сигнал необходимо преобразовать в у1(t) с законом распределения р1(y). Характеристику преобразования обозначим некоторым оператором D:
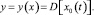 (1)
(1)
Линейный оператор обладает ограниченными возможностями преобразования, поэтому будем искать его в классе нелинейных преобразователей. При любом нелинейном однозначном преобразовании некоторому участку dx оси x соответствует некоторый участок dy оси y так, что
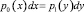
или
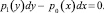 (2)
(2)
Данное уравнение является дифференциальным уравнением первого порядка с разделёнными переменными. Задача состоит в отыскании закона преобразования y = y(x).
Запишем уравнение (2) в виде
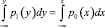 (3)
(3)
и для нормального распределения
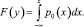 (4)
(4)
Смысл выражения (3) следующий: при заданных законах p0 и p1 зависимость y = y(x) должна быть подобрана так, чтобы интегральные функции их распределений совпадали.
В работе [4] приведены три примера, когда уравнение (3) может быть разрешено явно относительно y.
1. Сигнал x0(t) преобразуется к равномерному распределению
p1(y) = A; –a ≤ y ≤ a; x0 = 0.
Решение дает
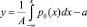 ; –a ≤ y ≤ a.
; –a ≤ y ≤ a.
2. Сигнал x0(t) преобразуется к релеевскому распределению
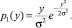
Решение дает
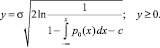
3. Сигнал x0(t) преобразуется к распределению гармонического колебания со случайной равномерно распределенной начальной фазой
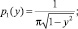 x0 = 0.
x0 = 0.
Решение дает
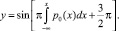
Маловероятно, что на практике мы встретим эти ситуации, они приведены скорее как иллюстрация того, как можно реализовать статистическое согласование законов распределения сигналов и помех. Однако ясно, что такое согласование в принципе возможно. Поскольку законы распределения – неотрицательные функции, то и производная от характеристики преобразования закона распределения будет неотрицательной, следовательно, и сами характеристики преобразования всегда монотонные однозначные функции. Для них обратные преобразования тоже однозначные и монотонные.
Рассмотрим два способа приближенного построения характеристик преобразования.
Если законы распределения заданы аналитически, то можно применить метод изоклин. Для этого уравнение (3) перепишем иначе
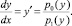 (5)
(5)
Придавая y/ различные постоянные значения k в интервале 0...∞, это уравнение можно разрешить относительно y. Кривые y(x, k) называются изоклинами. Данная кривая во всех точках может пересекаться искомой характеристикой под одним и тем же углом, тангенс которого равен k.
Для примера рассмотрим случай преобразования сигнала к нормальному распределению. Уравнение изоклины будет иметь следующий вид:
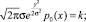
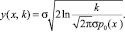
Придавая различные значения k, получим семейство изоклин. На каждой изоклине можно указать наклон характеристики в виде черточек, проведенных под углом, тангенс которого равен значению k для данной изоклины.
На рис. 1 изображено семейство изоклин с нанесенными на них наклонами для некоторого закона распределения p0(x).
Если семейство достаточно полное, то по нему нетрудно провести характеристику преобразования. Одна из них показана на рис. 1.
Когда законы распределения заданы графически, удобней применить метод кусочно-линейной аппроксимации.
На рис. 2 построена характеристика преобразования равномерно распределенного процесса к нормально распределенному процессу. Первую точку выберем на пересечении средних линий распределений (точка 0).
В пределах кривой p0(x) разбиваем ось х на малые отрезки, не обязательно равные. После выбора первой точки характеристики мы можем найти по формуле (5) касательную
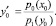
В числителе стоит ордината кривой в точке х0 , а в знаменателе – ордината кривой p1(y) в точке y0 , которые берем из рис. 2. Действительную кривую y = y(x) на участке 0...1 заменяем отрезком прямой, проведенным под углом, тангенс которого равен найденному значению 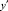 . Из точки 1 проводим прямую, параллельную оси абсцисс, и находим точку y1. Далее измеряем ординаты p0(x1) и p1(y1) и находим
. Из точки 1 проводим прямую, параллельную оси абсцисс, и находим точку y1. Далее измеряем ординаты p0(x1) и p1(y1) и находим
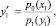
а по 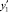 находим угол наклона касательной в точке 1 и проводим ее до точки 2. Затем из точки 2 проводим линию, параллельную оси абсцисс, и находим точку y2, равную y2 = y(x2). Далее измеряем ординаты p0(x2) и p1(y2) и находим соответствующее значение
находим угол наклона касательной в точке 1 и проводим ее до точки 2. Затем из точки 2 проводим линию, параллельную оси абсцисс, и находим точку y2, равную y2 = y(x2). Далее измеряем ординаты p0(x2) и p1(y2) и находим соответствующее значение 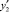 и так далее. Левую ветвь характеристики строим аналогично, двигаясь от точки 0 влево.
и так далее. Левую ветвь характеристики строим аналогично, двигаясь от точки 0 влево.
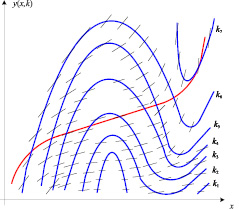
Рис. 1. Построение характеристики преобразования методом изоклин
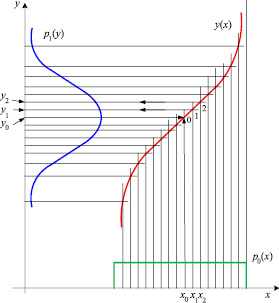
Рис. 2. Построение характеристики преобразования процесса с равномерным законом к нормальному закону
В сущности, этот метод есть тоже метод изоклин, но он не требует построения самих изоклин. Важно заметить, что при построении каждого отрезка мы используем действительные ординаты кривых в выбранной точке, поэтому не происходит накопление ошибок, допущенных на предыдущих отрезках характеристики.
Если теперь сместить p0(x) влево на величину х0, а p1(y) – вниз на величину y0, то характеристика без изменения наклона сместится так, что точка 0 совпадет с началом координат, и мы получим действительную характеристику.
Рецензенты:Сергеев Б.С., д.т.н., профессор кафедры «Электрические машины», Уральский государственный университет путей сообщения, г. Екатеринбург;
Иванов В.Э., д.т.н., профессор Института радиоэлектроники и информационных технологий, Уральский федеральный университет, г. Екатеринбург.
Работа поступила в редакцию 06.03.2015.
Библиографическая ссылка
Волынская А.В. О ДВУХ МЕТОДАХ ПРИБЛИЖЕННОГО ПОСТРОЕНИЯ ОПЕРАТОРА ПРЕОБРАЗОВАНИЯ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ // Фундаментальные исследования. 2015. № 2-7. С. 1383-1386;URL: https://fundamental-research.ru/ru/article/view?id=37158 (дата обращения: 26.12.2025).



