Рассмотрим методику группировки объектов для информационных процессов сложных систем на классы, к которым относятся объекты, наиболее близкие по своим характеристикам.
Эффективным механизмом объединения в группы объектов разнообразного функционирования по общим характеристикам является кластерный анализ [1, 2]. С использованием компьютерной техники кластерный анализ является одним направлений статистической науки.
Основной задачей кластерного анализа является определение групп схожих объектов в выборке данных (кластеров). Сходство количественных данных оценивается на основе понятия метрики при определении точки пространства на основе метрического расстояния между ними. Причем размерность пространства определяется числом характеристик, которые описывают объект [5].
Группа схожих объектов при выборке данных использует следующие кластерные методы:
– иерархические алгомеративные и дивизимные методы;
– итеративные методы группировки;
– факторные методы;
– поиск модальных значений плотности;
– сгущений;
– использования теории графов.
Применение различных методов к одним и тем же объектам может привести к сильно различающимся результатам.
Итеративные методы используют первичные данные, т.е. вычисления и хранения матрицы сходств между объектами, которые не требуется хранить. Следовательно, итеративные методы группировки позволяют обрабатывать большое множество при этом, осуществляют несколько просмотров данных и поэтому могут компенсировать последствия плохого исходного разбиения данных, что позволяет исключить главный недостаток иерархических алгомеративных методов. Данные методы формируют кластеры одного ранга, которые не могут быть вложенными, а следовательно, не могут быть частью иерархии и к тому же они не допускают перекрытия этих кластеров [2, 4].
Использование вышеописанных методов позволяет ограничить число итераций при определении принадлежности рассматриваемых объектов к тому или иному классу. В данном случае определяется минимальная совокупность объектов, переходящих из класса в класс, и тогда итерационный процесс прекращается и с определенной точностью рассматриваемые объекты объединены в кластеры.
На рисунке представлен процесс группирования данных итеративными методами.
Рассмотрим применение итеративного метода кластерного анализа к процессу группирования объектов базовой информации для информационных процессов сложных систем на основе значений параметров анализируемых характеристик [6].
Представим базовую информацию, циркулирующую в системе, в виде множеств
{Pi,j, Ai, Bj},
где 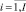 – индекс объектов, носителя первичной информации;
– индекс объектов, носителя первичной информации; 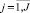 – индекс выбранных или всех характеристик объектов; Pi,j – количественное значение j-й характеристики i-го объекта; Ai – наименование i-гo объекта; Вj – наименование j-й характеристики.
– индекс выбранных или всех характеристик объектов; Pi,j – количественное значение j-й характеристики i-го объекта; Ai – наименование i-гo объекта; Вj – наименование j-й характеристики.
Все элементы Pi,j необходимо с точностью TI разбить на Кэ классов.
Значение TI определяет количество итераций. При увеличении количество итераций уменьшается количество шагов, но в то же время уменьшается точность разбиения, определяемая ЛПР. Значение Кэ также определяется ЛПР в зависимости от требуемой точности получения классификации разбиения (меньше Кэ – грубее классификация) [3, 7].
Чтобы в процессе исходного разбиения получить требуемое количество классов не меньше величины Кэ необходимо ввести масштабный коэффициент L. Масштабному коэффициенту L вначале присваивается значение равное 1.0. В том случае, если увеличить количество классов, L уменьшается и наоборот.
Алгоритм разбиения на классы представлен ниже:
0. Для формирования исходного разбиения на нужное число классов необходимо:
Сформировать множество {ri, di, ai, ki}размерностью I = 1,I:
ri – смешанный момент корреляции Карла Пирсона или угловая мера
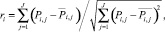
где 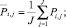
di – евклидово расстояние от начала координат до Pi,j
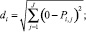
ai – индекс объекта в соответствии с Pi,j; ki – номер класса, к которому будет принадлежать i-й объект, первоначально все ki = 0.
1. Первоначальное разбиение на классы.
1.1. Для начала итеративного процесса:
– первоначально Ck = 0, k1 = 1, i = 1, Ci = 1;
– вычисляется среднее расстояние s между всеми элементами di:
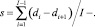
1.2. Вычисляется пороговое значение α, по которому определяется принадлежность i-го объекта к Ck классу:
– α = s∙L;
– i = Ci.
1.3. Вычисляется расстояние между очередным элементом и следующим:
Δd = di – d(i + 1).
1.4. Проверяется принадлежность i + 1 – го объекта к классу Ck.
Если Δd ≤ α, то k(i + 1) = Ck, i = i + 1 и:
– если i ≤ I,то переход к пункту 1.3;
– если i > I, то переход к пункту 1.5.
Если Δd > α, то Ck = Ck + 1, i = i + 1, Ci = i и переход к пункту 1.2.
1.5. Объединяются с использованием смешанного момента корреляции Карла Пирсона ri.
1.6. В начале:
– элементы {ri, ki} переупорядочиваются по возрастанию элементов ki и ri соответственно;
– первоначально определяются Ck = 1, Ckt = 1, k1 = 1, i = 1, Ci = 1.
1.7. Вычисляется пороговое значение α, по которому определяется принадлежность i + объекта Ci классу:
α = (ri – r(i + 1))∙L.
Если α = 0, то i = i + 1 и а вычисляется заново.
Если 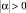 , то
, то 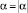 и i = Ci.
и i = Ci.
1.8. Проверяется, закончились ли объекты Ckt класса.
Если Ckt = ki, то переход к пункту 1.9.
ЕслиCkt ≠ ki , то Ckt = Ckt + 1, Ck = Ck + 1, i = i + 1, Ci = I и:
– если i > I, то переход к пункту 1.11;
– если i ≤ I, то переход к пункту 1.7.
1.9. Вычисляется расстояние между очередным и следующим элементами
Δr = ri – r(i + 1).
1.10. Проверяется принадлежность i + объекта к Ck классу:
Если Δr ≤ α , то k(i + 1) = Ck, i = i + 1, и:
– если i ≤ I, то переход к пункту 1.9;
– если i > I, то переход к пункту 1.11.
Если Δd > α, то Сk = Ck + 1, i = i + 1, Ci = i и переход к пункту 1.7.
1.11. Результаты Pi,j разбиты на «К» классов.
Если К = Кэ, то требуемое разбиение получено и переход к пункту 2 [1].
2. Если К > Кэ, то увеличивается параметр L и переход к пункту 1.1. Если К < Кэ, то уменьшается параметр L и переход к пункту 1.1.
3. Вычисляются 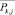 – центры тяжести полученных классов:
– центры тяжести полученных классов:
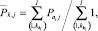
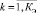 – индекс полученных классов.
– индекс полученных классов.
4. Проверяется, находится ли каждый объект в ближайшем классе.
4.1. Первоначально i = 1, n = 0.
4.2. Вычисляется квадрат отклонения объекта ai от центра тяжести всех классов:
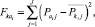
где 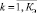 – индекс полученных классов;
– индекс полученных классов; 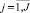 – индекс характеристики, участвовавшей в формировании результата Pi,jai объекта.
– индекс характеристики, участвовавшей в формировании результата Pi,jai объекта.
4.3. Если min(Fkai) достигается при k = ki, то объект ai находится в ближайшем классе, изменения его класса не происходит.
Если min(Fkai) достигается при k ≠ ki, то объект ai не находится в ближайшем классе, поэтому ki = k (класс объекта заменился на ближайший) и n = п + 1 (объект ai перешел в другой класс).
4.4. Увеличивается i = i + 1 и проверяется:
– если i > I, то закончился просмотр всех объектов и переход к пункту 5;
– если i ≤ I, то переход к пункту 4.2.

Процесс группирования данных итеративными методами
5. Если 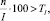 то требуемая точность итеративного процесса не достигнута и переход к пункту 2.
то требуемая точность итеративного процесса не достигнута и переход к пункту 2.
Если 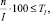 то требуемая точность итеративного процесса достигнута. Получено окончательное разбиение Pi,j по классам.
то требуемая точность итеративного процесса достигнута. Получено окончательное разбиение Pi,j по классам.
К исходным данными разбиения объектов на классы относятся: 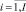 – индекс объекта;
– индекс объекта; 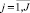 – индекс характеристики объекта; Pi,j – количественное значение j-й характеристики i-го; Ai – наименование i-го объекта; Bj– наименование j-й характеристики; TI – точность разбиения в процентах; Кэ – количество классов разбиения.
– индекс характеристики объекта; Pi,j – количественное значение j-й характеристики i-го; Ai – наименование i-го объекта; Bj– наименование j-й характеристики; TI – точность разбиения в процентах; Кэ – количество классов разбиения.
Результатом разбиения объектов на классы являются: К – количество полученных классов; 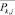 – центры тяжести полученных классов; ki – номер класса, к которому принадлежит i-й объект; ai – индекс объекта в соответствии с Pi,j.
– центры тяжести полученных классов; ki – номер класса, к которому принадлежит i-й объект; ai – индекс объекта в соответствии с Pi,j.
Филатов Г.Ф., д.ф.-м.н., профессор кафедры математики Военного учебного научного центра Военно-воздушных сил, «Военно-воздушная академия имени профессора Н.Е. Жуковского и Ю.А. Гагарина», г. Воронеж;
Чопоров О.Н., д.т.н., профессор, проректор по научной работе Воронежского института высоких технологий, г. Воронеж.
Работа поступила в редакцию 02.03.2015.
Библиографическая ссылка
Сумин В.И., Дыбова М.А., Смоленцева Т.Е. МЕТОДИКА ГРУППИРОВАНИЯ БАЗОВОЙ ИНФОРМАЦИИ ДЛЯ ИНФОРМАЦИОННЫХ ПРОЦЕССОВ СЛОЖНЫХ СИСТЕМ // Фундаментальные исследования. 2015. № 2-5. С. 931-934;URL: https://fundamental-research.ru/ru/article/view?id=36959 (дата обращения: 30.01.2026).



