К синусоидально возрастающим ПП в области испытаний мощных СМ относятся опыты ВН и УВ. Из осциллограмм данных опытов по методам отечественных стандартов получают электромагнитные ПВ и параметры СМ. В условиях эксплуатации мощных СМ для получения ПВ и параметров не всегда удаётся осуществить центральный опыт внезапного симметричного короткого замыкания, поэтому после него наиболее пригодным является опыт ВН. Но при обработке осциллограммы ВН возникают проблемы с определением малых начальных значений напряжений сверхпереходной и переходной составляющих и ПВ, так как идентификация сверхпереходной составляющей требует увеличения периода записи, а переходной составляющей – уменьшение его в несколько раз из-за достижения напряжения ПП до 3/4 установившегося значения (в мощных СМ на это требуется свыше10 с).
В статье показаны возможности разработанных ВСМ [1–8] для исследования и идентификации с высокой точностью и достоверностью возрастающих ПП в опытах ВН и УВ, несмотря на проблемы, возникающие при обработке таких процессов по ГОСТу.
Исходные данные для апробации ВСМ получены по результатам стендовых испытаний СМ типа ТТК-110-2-П мощностью 110 МВт после отключения установившегося симметричного короткого замыкания в опыте ВКЗ. В результате чего в обмотке статора возник ПП в виде возрастающего напряжения. На рис. 1 приведена аналоговая информация ПП ВН, преобразованная с помощью интеллектуального ЦЗО в дискретную с высокой точностью (10000 выборок за период с длительностью выборки равной 40 мкс), которая сохраняется в автономной памяти ЦЗО для дальнейшего анализа и обработки. Для выделения вершин ПП информацию из памяти ЦЗО переносят в ЭВМ с целью преобразовывания, сжатия и сглаживания кубическим сплайном по стандартной программе (рис. 2).
Выделение вершин осуществляется последовательным сравнением на выполнение неравенства между соседними дискретно заданными значениями напряжений выборок, в результате ПП оказывается представленным в виде дискретных огибающих в узлах дискретизации с частотой 50 Гц (рис. 3).
Возрастающий ПП можно представить дискретными элементами напряжения между обеими огибающими, при этом первый элемент иоj на первом шаге рассчитывают по унифицированным выражениям в [1]:
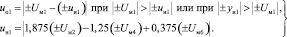 , (1)
, (1)
а последующие элементы иоj со второго шага рассчитываются с видоизмененными интерполяционными коэффициентами при 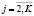 с шагом 0,01 с
с шагом 0,01 с
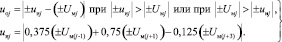 (2)
(2)
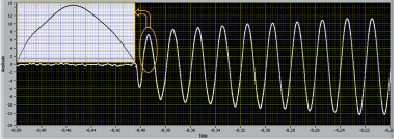
Рис. 1. Дискретный ПП с выхода ЦЗО
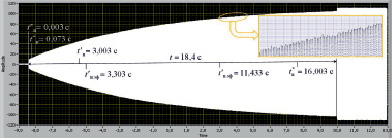
Рис. 2. Полный ПП в опыте ВН СМ
В формуле (1) интерполяционное значение напряжения ии1 рассчитывается по 2-й, 4-й и 6-й вершинами напряжения якоря. Выведенные коэффициенты 1,875, 1,25, 0,375 на базе интерполяционной схемы Эйткена реализуют процедуру интерполяции второго порядка назад.
Аналогично выведенные коэффициенты 0,375, 0,75, 0,125 позволяют по формуле (2) рассчитать по трем амплитудным значениям напряжения якоря Uм(j – 1), Uм(j + 1), Uм(j + 3) между соседними вершинами дополнительные значения ииj, принадлежащие огибающим напряжения якоря, реализуя скользящую интерполяцию вперед. При расположении первой вершины тока якоря над осью нечетная последовательность вершин в интерполяционном выражении напряжения ииj обеспечивает получение верхней огибающей в узлах дискретизации, а четная последовательность – нижней огибающей.
Преобразованный в виде элементов ПП представлен на рис. 4. На рис. 5 пояснено получение элементов по формулам (1), (2). Перевод дискретно возрастающего ПП в затухающий осуществляется вычитанием из установившегося значения текущих на каждом шаге при 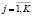 .
.
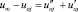 . (3)
. (3)
Разность по (3) представляет собой сумму сверхпереходной и переходной составляющих в узлах дискретизации, затухающей с шагом 0,01 с (см. рис. 6).
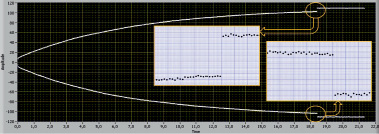
Рис. 3. Представление дискретно возрастающего ПП вершинами с шагом 0,02 с
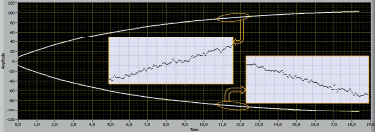
Рис. 4. ПП, заданный элементами между обеими огибающими с шагом дискретизации 0,01 с
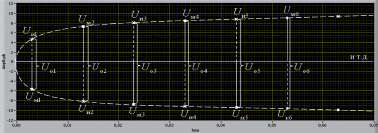
Рис. 5. К пояснению получения дискретных элементов между обеими огибающими ПП с шагом 0,01 с по формулам (1), (2)
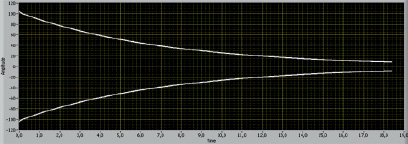
Рис. 6. Преобразованный ПП из возрастающего в затухающий
Разделение и идентификация данных составляющих осуществляются по разработанному ВСМ для затухающих ПП СМ с широким использованием эффективных точечных выборок, используемых для конструирования основных формул и для проведения исследований по оценке погрешности и анализа результатов идентификации. Алгоритм реализации операций по разделению составляющих ПП включает:
- Обоснование границ
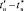 для выделения диапазона ПП с одной переходной составляющей.
для выделения диапазона ПП с одной переходной составляющей. - Исследования по оценке погрешности отклонения переходной составляющей от экспоненциального закона в диапазоне
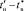 ПП с использованием минимизированного объёма эффективных точечных выборок.
ПП с использованием минимизированного объёма эффективных точечных выборок. - Оптимизацию установившегося значения ПП.
- Идентификацию переходной составляющей ПП.
- Идентификацию сверхпереходной составляющей ПП.
- Оценку погрешности идентификации всего ПП.
- Определение параметров СМ по результатам обработки осциллограммы.
В первой процедуре алгоритма нижняя граница задаётся по условию 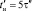 в [1] верхнюю границу
в [1] верхнюю границу  выбирают по достижению напряжения ПП до 3/4 установившегося значения (рис. 2).
выбирают по достижению напряжения ПП до 3/4 установившегося значения (рис. 2).
Во второй процедуре алгоритма на базе случайного признака (5) в [2] и по сконструированным формулам (6)–(11) в [1] с использованием элементов объемом n = 2 в диапазоне 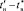 ПП формируются генеральная совокупность случайного признака объёмом N, выборка из него объёмом nв и в качестве базы (для сравнения параметров названных объёмов) формируется минимизированный объём эффективных точечных выборок объёмом nэф с определением их параметров
ПП формируются генеральная совокупность случайного признака объёмом N, выборка из него объёмом nв и в качестве базы (для сравнения параметров названных объёмов) формируется минимизированный объём эффективных точечных выборок объёмом nэф с определением их параметров 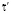 (математическое ожидание – МО) и σ2 (дисперсия):
(математическое ожидание – МО) и σ2 (дисперсия):
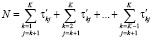 , (4)
, (4)
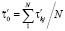 ,
, 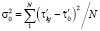 , (5)
, (5)
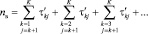 , (6)
, (6)
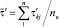 ,
, 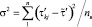 , (7)
, (7)
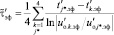 ,
,
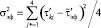 . (8)
. (8)
В формуле (8) k = 1,2,3,4 – переменная для задания нижней границы, т.е. 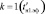 ,
, 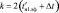 ,
, 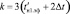 ,
, 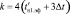 с соответствующими элементами
с соответствующими элементами 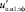 ,
, 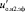 ,
, 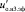 ,
, 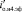 ; j* – переменная для определения верхней границы t′в.эф по условию (16) в [1] u′о.в1эф = 0,33u′о.н1.эф(t′в.1эф), u′о.в2эф = 0,33u′о.н2.эф(t′в.2эф), u′о.в3эф = 0,33u′о.н3.эф(t′в.3эф), u′о.в4эф = 0,33u′о.н4.эф(t′в.4эф), всегда меньше
; j* – переменная для определения верхней границы t′в.эф по условию (16) в [1] u′о.в1эф = 0,33u′о.н1.эф(t′в.1эф), u′о.в2эф = 0,33u′о.н2.эф(t′в.2эф), u′о.в3эф = 0,33u′о.н3.эф(t′в.3эф), u′о.в4эф = 0,33u′о.н4.эф(t′в.4эф), всегда меньше  исследуемой переходной составляющей в обоснованных границах
исследуемой переходной составляющей в обоснованных границах 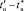 (рис. 2).
(рис. 2).
Совокупности случайного признака объёмом N и nв упорядочиваются по возрастанию от минимальной величины случайного признака до максимальной (или по убыванию), образуя вариационные ряды. Относительные отклонения минимальных и максимальных значений случайного признака между собой или от МО характеризуют размах вариационных рядов. Анализ полученных оценок размаха вариационных рядов, а также оценок их дисперсий σ2 позволяют судить о степени отклонения составляющих ПП от экспоненциального (таблица).
В третьей процедуре алгоритма оптимизация установившегося значения ПП осуществляется по выражению (16) в [1], которое представляет собой статистическую функцию с реализацией операций моделирования переходной составляющей с заданным шагом на участке ПП 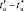 с вариацией установившегося значения и нижней границы одновременно с процедурой минимизации погрешности приближения модели к опытным данным затухающего ПП
с вариацией установившегося значения и нижней границы одновременно с процедурой минимизации погрешности приближения модели к опытным данным затухающего ПП
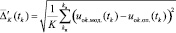 . (9)
. (9)
Оптимизация установившегося значения завершается представлением среднеквадратичной погрешности приближения модели переходной составляющей к опытным данным в виде поверхности в трёхмерной системе координат. В итоге алгоритмически определяются границы эффективных точечных выборок, величина электромагнитной ПВ, начальное значение переходной составляющей, рассчитанные по минимизированному объёму эффективных точечных выборок и обеспечивающие по (9) минимальную погрешность приближения (рис. 7).
В четвёртой процедуре алгоритма идентификация переходной составляющей рассчитана по опытным данным ПП в диапазоне 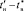 по (11), (15) в [1] с использованием минимизированного объёма nэф = 4 эффективных точечных выборок.
по (11), (15) в [1] с использованием минимизированного объёма nэф = 4 эффективных точечных выборок.
В пятой процедуре алгоритма идентификация сверхпереходной составляющей ПП реализована по исходным данным сверхпереходной составляющей 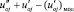 с использованием нижней границы
с использованием нижней границы 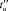 , соответствующей первому элементу ПП по рис. 2, с использованием эффективных точечных выборок. В зависимости от уровня зашумлённости ПП предусмотрены варианты идентификации данной составляющей.
, соответствующей первому элементу ПП по рис. 2, с использованием эффективных точечных выборок. В зависимости от уровня зашумлённости ПП предусмотрены варианты идентификации данной составляющей.
В шестой процедуре алгоритма представлена оценка погрешности идентификации всего ПП по результатам приближения его модели к опытным данным в узлах дискретизации в диапазоне от 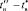
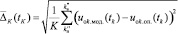 , (10)
, (10)
где моделью является сумма идентифицированных переходной и сверхпереходной составляющих ПП.
В седьмой процедуре алгоритма рассчитываются параметры 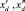 по известным формулам в стандартах.
по известным формулам в стандартах.
В таблице представлена информация о степени отклонения ПП от экспоненциального затухания и результаты идентификации ПП в опыте ВН для СМ на 110 МВт.
Исследования и идентификация ПП ВН выполнены с использованием программно-инструментальной среды LabVIEW и электронных таблиц Excel.
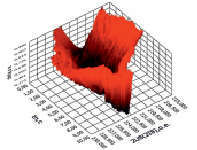 а)
а) 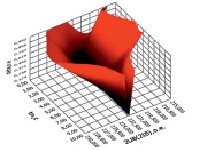 б)
б)
Рис. 7. Среднеквадратичная поверхность приближения 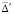 в диапазоне ПП
в диапазоне ПП 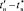 переходной составляющей: а – по опыту; б – для модели
переходной составляющей: а – по опыту; б – для модели
|
Результаты исследования переходной составляющей на отклонение от экспоненциальности |
|||||
|
Объем |
МО |
Дисперсия |
Размах случайного признака, % |
||
|
вариационных рядов |
от МО |
||||
|
Генеральная совокупность τ´kj |
N = 8512 |
|
|
96÷2546 |
68÷734 |
|
Выборка из ген. совокупности |
nв = 2187 |
|
σ2 = 0,0304 |
46÷87 |
28÷34 |
|
Объем эф. точечных выборок |
nэф = 4 |
|
|
1 |
1 |
|
Результаты идентификации |
|||||
|
Переходная составляющая |
Сверхпереходная составляющая |
||||
|
Диапазон, с |
( |
( |
|||
|
Постоянная времени, с |
7,317610 |
0,059326 |
|||
|
Начальное значение, о.е. |
202,159 |
8,702 |
|||
|
Установившееся значение, о.е. |
222,3 |
||||
|
Среднеквадратичное отклонение, о.е. |
|
– |
|||
|
Среднеквадратичное отклонение по всему процессу, о.е. |
|
||||
Выводы
1. ВСМ подтверждают их эффективное использование для исследования и идентификации возрастающих ПП мощных СМ в опытах ВН, УВ. Для опытов УВ при замкнутой обмотке статора в используемых формулах и зависимостях следует вместо напряжений подставлять токи.
2. ВСМ с использованием ЦЗО и современных электронно-вычислительных средств для исследования и экспресс-обработки ПП мощных СМ по программе приёмочных стендовых испытаний трудоёмкость обработки (особенно при выделении вершин) снижается в десятки и сотни раз.
3. ВСМ исследования и идентификации ПП мощных СМ обеспечивают высокую точность и достоверность оценочных результатов идентификации в условиях влияния различных случайных факторов на ПП.
4. ВСМ позволяют на высоком уровне проводить погрешностный анализ различных идентифицируемых составляющих ПП мощных СМ.
5. ВСМ благодаря использованию ЦЗО позволяют в отличии от методов отечественных стандартов идентифицировать ПП мощных СМ без проблем из единой записи при любой длительности их протекания.
Рецензенты:
Кавалеров Б.В., д.т.н., доцент, заведующий кафедрой «Электротехника и электромеханика», Пермский национальный исследовательский политехнический университет, г. Пермь;
Цаплин А.И., д.т.н., профессор, заведующий кафедрой «Общая физика», Пермский национальный исследовательский политехнический университет, г. Пермь.
Работа поступила в редакцию 29.12.2014.
Библиографическая ссылка
Чабанов Е.А., Судаков А.И., Турпак А.М., Лоскутников В.А. ВЕРОЯТНОСТНО-СТАТИСТИЧЕСКИЕ МЕТОДЫ ИДЕНТИФИКАЦИИ СИНУСОИДАЛЬНО ВОЗРАСТАЮЩИХ ПЕРЕХОДНЫХ ПРОЦЕССОВ СИНХРОННЫХ МАШИН // Фундаментальные исследования. 2014. № 12-10. С. 2135-2141;URL: https://fundamental-research.ru/ru/article/view?id=36539 (дата обращения: 06.07.2025).




 = 7,214161
= 7,214161
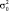 = 1,054
= 1,054
 = 7,206968
= 7,206968
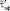 = 7,237067
= 7,237067
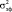 = 0,0008
= 0,0008
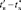 ) = 3,003 – 16,003
) = 3,003 – 16,003
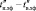 ) = 0,003 – 0,073
) = 0,003 – 0,073
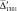 = 0,285 (0,141 %)
= 0,285 (0,141 %)
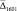 = 0,546 (0,245 %)
= 0,546 (0,245 %)