При реализации эффективного и качественного функционирования любого хозяйствующего субъекта, будь то вуз или материальное производство, имеет смысл применять методы и средства автоматизированных систем управления (АСУ). Одной из основных функциональных составляющих любой АСУ является база данных (БД), а также набор средств и методов доступа, которые предоставляет система управления базами данных (СУБД).
При анализе данных АСУ ряда прикладных областей имеет место вывод о том, что количество значений большинства полей значительно меньше, чем количество записей в БД. Так, в мебельном производстве, большую часть записи в АСУ составляют такие значения как номер смены, участок, наименование детали, сорт, категория влажности и т.д. Все они имеют небольшое количество значений. В АСУ вуза ситуация аналогичная. Например, студентов в вузе может обучаться тысячи, в то время как форм обучения всего три (рис. 1).
Структуры данных АСУ вуза в Российской Федерации концептуально следуют из законодательных актов и нормативных документов, основным является [1]. Анализ законодательства в контексте структур данных АСУ вуза выполнены в [6, 7]. Особенности мебельного производства подробно рассмотрены в [2, 5].
Формулирование общих зависимостей в моделях данных позволит сгенерировать особые алгоритмы функционирования СУБД, применение которых повысит эффективность функционирования базы данных. Общие концепции баз данных, реляционных таблиц и языка запросов T-SQL рассмотрены в [3, 4].
Рис. 1.
Исходное отношение Q (слева) и отсортированное Qsort (справа)
|
N |
a |
b |
|
1 |
a1 |
b1 |
|
2 |
a1 |
b2 |
|
3 |
a1 |
b1 |
|
4 |
a2 |
b2 |
|
5 |
a2 |
b2 |
|
6 |
a2 |
b1 |
|
7 |
a1 |
b2 |
|
8 |
a1 |
b1 |
|
N |
Np |
a |
b |
|
1 |
1 |
a1 |
b1 |
|
3 |
2 |
a1 |
b1 |
|
8 |
3 |
a1 |
b1 |
|
2 |
4 |
a1 |
b2 |
|
7 |
5 |
a1 |
b2 |
|
6 |
6 |
a2 |
b1 |
|
4 |
7 |
a2 |
b2 |
|
5 |
8 |
a2 |
b2 |
В таблице (слева) представлено отношение Q, которое обладает всеми свойствами базы данных АСУ вуза или АСУ мебельного производства. Количество значений полей a и b значительно меньше, чем количество записей в базе данных. Поле N отображает те поля таблиц, количество значений которых соизмеримо с количеством записей в БД или уникально.
Отсортируем исходное отношение по неубыванию с сохранением исходной нумерации N, добавим нумерации отсортированного отношения Np (таблица, справа) и запишем в новую таблицу (усовершенствованный индекс – отношение Ia, схема 1, справа) только уникальные значения дескрипторов. В дополнительном поле перечислим адреса участков памяти в исходном отношении, в которых данное значение встречается. В результате для выборки произвольных значений a и b в исходном отношении, необходимо просмотреть все исходное отношение. Воспользовавшись усовершенствованным индексом, необходимо просмотреть в среднем половину усовершенствованного индекса, т.к. он отсортирован по неубыванию. Конечно, в конкретных случаях распределение вероятностей может быть неравномерным. Так, если вероятность выборки любой записи исходного отношения Q равновероятна и равна (100/8) % = 12,5 %, то сравнение искомого значения с первой строчкой в усовершенствованном индексе снизит неопределенность на (12,5*3) % = 37,5 % (по количеству указателей в поле ptr), а сравнение искомого значения с 3-й строчкой снизит неопределённость только на 12,5 %. Тем не менее, допустим, что распределение вероятностей в Ia равномерно, тогда можно сказать, что для поиска произвольной записи стандартным методом необходимо просмотреть все 8 записей исходного отношения Q, а с использованием усовершенствованного индекса Ia необходимо просмотреть, в среднем, 2 записи (схема 1).
Использование усовершенствованного индекса Ia уже дает значительный эффект. На отношении Q прирост производительности в среднем в четыре раза.
На количество записей в индексе Ia влияет не количество записей в исходном отношении, а количество значений дескрипторов. Таким образом, рост количества записей в исходном отношении на время поиска практически не влияет.
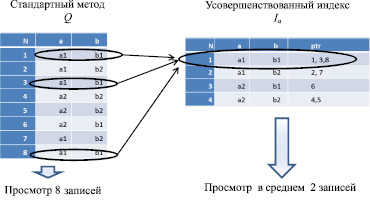
Схема 1. Стандартный метод выборки и усовершенствованный индекс
Пусть count(I) – количество записей в усовершенствованном индексе Ia.
di – количество значений i-го дескриптора
n – Количество дескрипторов.
Тогда по правилам комбинаторики, и с учетом того, что в исходном множестве могут находиться не все возможные комбинации дескрипторов, имеем:
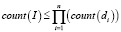 . (1)
. (1)
Таким образом, при условии, что количество значений дескриптора значительно меньше, чем количество записей в исходном отношении Q, выполняется неравенство count(Q) >> count (I), где count (Q) – количество записей в исходном отношении Q.
Усовершенствованный индекс Ia имеет ряд недостатков, таких как:
1. Избыточность (в приведенном примере Ia хранит в памяти по два экземпляра каждого значения дескриптора),
2. Зависимость схемы индексной таблицы от схемы исходного отношения (поля a и b),
3. Поле указателей ptr имеет переменную длину, зависящую от количества записей в исходном отношении, что может порождать фрагментацию памяти, а его обработка вынуждает применять побитовые операции для вычленения адресов из битовой последовательности, что напрямую замедляет работу.
Таким образом, хранить индекс Ia в памяти компьютера неэффективно. Сформируем указатели, которые однозначно определяют усовершенствованный индекс Ia и лишены обозначенных недостатков.
Указатель U0 состоит из двух указателей U01 и U02 и является вспомогательным указателем.
Указатель U01 (пример для Ia)
|
1 |
a1 |
1 |
|
2 |
a2 |
2 |
|
3 |
b1 |
1 |
|
4 |
b2 |
2 |
1-й столбец – номер значения дескриптора,
2-й столбец – значение дескриптора,
3-й столбец – соответствующее данному значению дескриптора целочисленное значение.
Данный указатель ставит в соответствие каждому значению дескриптора целое число от 1 до ni, где ni – количество значений i-го дескриптора.
Указатель U02 (пример для Ia)
|
1 |
a |
1 |
|
2 |
b |
3 |
|
3 |
null |
5 |
1-й столбец – номер дескриптора,
2-й столбец – название дескриптора,
3-й столбец – номер значений дескриптора в U01, с которого начинаются значения данного дескриптора. Номер конца интервала определяется следующей соответствующей записью в U02 минус единица.
Последняя запись в U02 служит для определения последней записи в U01.
Указатель U02 служит для определения, какому интервалу в U01 какой дескриптор соответствует.
Указатель U1 является основным указателем и определяет индекс Ia, отражая его основные структурные составляющие.
U1 состоит из фиксированного количества столбцов:
1-й столбец – целочисленное значение хэш-функции, однозначно определяющее данную совокупность значений дескрипторов.
К подбору хеш-функции следует подойти особенно тщательно. Необходимо полностью исключить возможность коллизий. Неплохо себя показывает в данном качестве следующая хэш-функция:
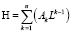 , (2)
, (2)
где n – количество дескрипторов,
L – максимальное количество значений дескриптора среди всех дескрипторов отношения,
Ak – целочисленное значение k-го дескриптора (из U01).
Выбор в качестве L максимального количества значений дескрипторов в отношении гарантирует отсутствие коллизий, при этом формируя разряженное поле значений хэш-функции. Неиспользуемые интервалы объясняются двумя причинами:
1. Когда количество значений какого-либо дескриптора меньше максимального, соответствующее числовое поле не используется. Заполняется в случае увеличения количества значений дескриптора.
2. Когда какая-либо комбинация существующих значений дескриптора не встречается в исходном множестве. Заполняется в случае включения в БД записей с такой комбинацией.
Наличие пустых интервалов может подсказать СУБД и оператору базы данных, что данные области могут заполняться по мере наполнения базы данных, что может сделать целесообразным оставление пустых участков на соответствующих страницах памяти ЭВМ для дальнейшего заполнения без фрагментации.
С учетом того, что значение данного поля – целое, уникальное, возрастающее число, его можно использовать в качестве первичного ключа при погружении данного указателя в реляционные таблицы базы данных.
2-й столбец – указатель на область памяти, содержащую записи с данными значениями дескриптора.
Рассмотрим поле ptr индекса Ia (схема 1, справа) первой записи. Оно содержит числа 1,3,8 – указатели на исходное неотсортированное множество. В данном векторе нет зависимостей. Но если рассмотреть отсортированное исходное отношение Qsort, то первые три записи имеют значение полей N 1,3,8, а значения полей Np 1,2,3. Таким образом, номера строк в отсортированном индексе могут однозначно отобразить интервал целых чисел Np. Будем хранить во 2-м столбце U1 значение Np первого вхождения данной совокупности значений дескриптора. Для определения окончания интервала при поиске, необходимо считать следующую строчку в Np и отнять единицу из соответствующего поля. Если следующая строчка отсутствует, то адрес окончания интервала совпадает с количеством записей исходного отношения Q.
Построим указатель U1 для Ia:
|
3 |
1 |
|
4 |
4 |
|
5 |
6 |
|
6 |
7 |
Пример поиска значений двух дескрипторов.
Пусть необходимо найти значение a = a1 и b = b2.
1. По указателю U02 узнаем, что порядковый номер дескриптора a равен 1, b равен 2 (1-й столбец U02). Область распределения значений в U01 дескриптора a – 1..2, b – 3..4 (2-й столбец U02).
2. Пользуясь информацией, полученной на предыдущем шаге, находим в U01, что целочисленное для a1 = 1, для b2 = 2.
3. Пользуясь информацией, полученной на двух предыдущих шагах, а также зная максимальное количество значений дескриптора среди представленных, вычисляем хэш-значение для искомой последовательности:
H = 1*2^1+2*2^0 = 4.
4. Находим в 1-столбце U1полученное значение. Если оно отсутствует, значит такого значения нет в исходном отношении Q. В нашем случае оно имеется. Считываем соответствующий указатель из второго столбца (в данном случае – 4). Считываем значение 2-го столбца следующей строки указателя U1, вычитаем единицу из полученного значения (6 – 1 = 5).
5. Считываем из Qsort строки, Np которых находится в диапазоне 4..5.
Результат получен.
С точки зрения оптимизации вычислений, имеет смысл в третьем столбце указателя U01 размещать не целочисленное значение, соответствующее значению дескриптора, а готовое слагаемое из (2). В таком случае более ресурсоемкие операции умножения и возведения в степень можно будет осуществить в момент построения индекса однократно, а в процессе эксплуатации БД собирать хэш путем суммирования готовых значений из третьего столбца модифицированного указателя U01мод.
Пример модифицированного указателя U01мод (для Ia)
|
1 |
a1 |
2 |
|
2 |
a2 |
4 |
|
3 |
b1 |
1 |
|
4 |
b2 |
2 |
1-й столбец – номер значения дескриптора,
2-й столбец – значение дескриптора,
3-й столбец – соответствующее данному значению дескриптора целочисленное значение для суммирования в хэш-функцию. Численно равно выражению (AkLk –1) из формулы (2).
Для практической апробации усовершенствованного индекса был настроен экспериментальный стенд, в котором формировалось случайным образом заполненное исходное отношение с последующими поисковыми запросами по стандартному методу и по методу усовершенствованного индекса. Результаты работы заносились в журнал, затем они были проанализированы и подвергнуты регрессионному анализу по методу наименьших квадратов.
Алгоритм усовершенствованного индекса был реализован в виде программы для ЭВМ на языке программирования C#.
В программном обеспечении стенда использовались профессиональные программные пакеты Microsoft: Microsoft SQL Server Express (64-bit) , версия 11.0.3128.0; Microsoft Visual Studio Premium 2012 версии 4.5.51641.
На рис. 2 представлен график результатов проведенного эксперимента.
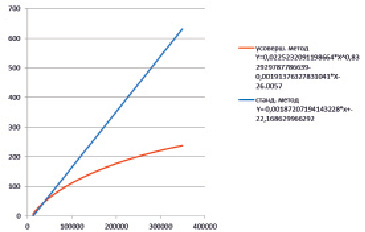
Рис. 2.
По оси x откладывается количество записей в БД на момент запроса, по оси y – время обработки выборки произвольных значений дескрипторов.
На графике прослеживается, что на момент начала эксперимента, когда количество записей невелико, усовершенствованный метод несколько проигрывает в эффективности стандартному методу. Это обусловлено накладными расходами по реализации алгоритма. С ростом количества записей, когда начинает выполняться правило значительного превосходства количества записей над количеством значений дескриптора, разница в эффективности функционирования между стандартным и усовершенствованным методом становится значительной в пользу усовершенствованного метода.
Таким образом, в данной статье проанализированы концептуальные позиции структур данных АСУ вуза и АСУ мебельного производства. Предложены алгоритмы организации и доступа к данным, позволяющие повысить эффективность обработки данных и, как следствие, повысить эффективность функционирования АСУ в целом. Теоретические выводы экспериментально подтверждены.
Рецензенты:
Лабунец В.Г., д.т.н., профессор, заведущий кафедрой ФГАОУ ВПО «УрФУ имени первого Президента России Б.Н. Ельцина», г. Екатеринбург;
Бутко Г.П., д.э.н., профессор, заведующий кафедрой НОУ ВПО «Уральский Финансово-Юридический институт», г. Екатеринбург.
Работа поступила в редакцию 29.12.2014.
Библиографическая ссылка
Стаин Д.А., Часовских В.П. МЕТОДЫ ОПТИМИЗАЦИИ И ПОВЫШЕНИЯ ЭФФЕКТИВНОСТИ ДОСТУПА К ДАННЫМ В ИНФОРМАЦИОННЫХ СИСТЕМАХ УПРАВЛЕНИЯ ОРГАНИЗАЦИЕЙ // Фундаментальные исследования. 2014. № 12-10. С. 2114-2119;URL: https://fundamental-research.ru/ru/article/view?id=36535 (дата обращения: 16.11.2025).



