Технологии изготовления МЭМС позволяют производить достаточно точные миниатюрные датчики для измерения механических величин мобильных объектов управления (роботов, беспилотных управляемых аппаратов и т.п.). На практике сигналы датчиков искажаются помехами, что дает значительный уровень погрешности в измерениях. В связи с этим вопросы обеспечения точности измерительных систем при их работе в условиях реальной среды представляются одними из важнейших. Точность информационного обеспечения во многом определяет возможности реализации эффективного управления подвижными объектами. Для ослабления помех необходимо применять дополнительные меры преобразования и обработки сигналов.
В литературе активно обсуждаются вопросы разработки и исследования МЭМС для измерения механических величин [1, 3–6, 8, 9, 10–12], в том числе в условиях случайных измеряемых физических процессов и при воздействии помех. С этой целью уже разработаны технологии оптимальной обработки сигналов, способные функционировать в условиях случайной среды [6, 8, 11, 13, 14]. Обеспечению статической и динамической точности МЭМС посвящено множество статей. В статьях [4, 9] для различных МЭМС были сформулированы требования к параметрам корректирующего устройства (КУ) типа ПИД регулятора из условия обеспечения минимальных значений динамических ошибок.
Производится учет условий реальной среды, предполагающей случайные отклонения измеряемых механических величин от стационарных значений и воздействие случайных помех при измерениях. При синтезе стохастических фильтров обычно помехи считают в виде винеровского процесса [13]. Часто измерительные шумы также рассматривают широкополосными случайными вибрациями (ШСВ), имеющими большое сходство с белыми шумами. Кроме того, при измерении механических величин выделяют режим медленно и быстро меняющихся процессов (то и другое свойственно динамическим объектам управления). При этих условиях в статье [6] отмечалась эффективность применения традиционного калмановского алгоритма фильтрации для оценивания полезных процессов в МЭМС широкого применения (акселерометрах и датчиков угловых скоростей – ДУС).
В статье [11] для измерения продольного и вертикального ускорения автомобиля при эксплуатационных испытаниях использовался акселерометр с фильтром Калмана, причем мощность помех, искажающих информацию, считалась достаточно малой.
В продолжение исследований применения фильтра Калмана в измерительных системах в статье [8] представлен алгоритм получения оптимальных оценок при помехах в виде ШСВ. В статье были определены условия эффективности микроэлектромеханической системы – микрогироскопа. Экспериментальное исследование проводилось на основе программного обеспечения Matlab с использованием опубликованных ранее алгоритмов моделирования МЭМС ДУС со случайными сигналами [5].
Вышла в свет еще одна статья, касающаяся применения МЭМС в комплексной системе обработки информации в условиях измерительных шумов [7]. В статье сформулированы требования к параметрам МЭМС с перекрестными связями на основе критерия точности при использовании принципа инвариантности. Было проведено исследование эффективности работы комплексной МЭМС в условиях возмущенной среды (при воздействии интенсивных помех) и даны рекомендации по выбору субоптимального алгоритма фильтрации. Рассматриваемая в статье математическая модель комплексной МЭМС адекватно отражает реальную систему измерения дальности и скорости подвижного летательного аппарата. Полученные в статье результаты исследования по влиянию помех на динамическую точность комплексной системы позволяют выполнить достаточно эффективную фильтрацию и получить приемлемые среднеквадратические ошибки (СКО) оценок дальности и скорости.
Постановка задачи
Рассмотренный в статье [7] алгоритм комплексной обработки информации в МЭМС является всего лишь субоптимальным и не дает минимально возможных СКО. Интересным является применение традиционного алгоритма Калмана для комплексной обработки информации при оценивании скорости и дальности подвижного объекта относительно цели. В этом случае следует ожидать достижения минимальных СКО. В данной статье ставится задача разработки математической модели подвижного объекта и процесса наблюдения за целью в векторно-матричной форме, подходящей для проектирования фильтра Калмана. Все исходные данные, принятые в статье [7], при этом остаются действующими.
При исследовании используется гипотеза о некоррелированности шумов с измеряемыми процессами. Все процессы предполагаются стационарными, эргодическими с нормальными законами распределения. В фазовый вектор фильтра Калмана кроме переменных состояния подвижного объекта придется включить еще и переменные для случайных составляющих измеряемого процесса и шумовых процессов. Задачей исследования фильтра Калмана в данном случае является определение предельной ошибки при различных соотношениях мощности сигнала к мощности помех. Экспериментальное исследование измерительной системы проводится так же, как и в работе [7], на основе программного обеспечения Matlab.
Применение фильтрации Калмана для перекрестной схемы обработки сигналов датчиков сопряжено с необходимостью выделения объекта наблюдения и каналов измерения в традиционном виде (рис. 1).
На схеме обозначено U – вектор входных сигналов (в данном случае это ускорение, получаемое с микроакселерометра и дальность, получаемая с радиодальномера); N – вектор измерительных шумов, присущих измерителю скорости и измерителю дальности (цветные шумы); H – вектор выходных сигналов объекта наблюдения, т.е. скорости подвижного объекта и дальности цели; Y – вектор измерений скорости и дальности; He – вектор выходных сигналов фильтра.
Математическая модель комплексной системы
Построение математической модели объекта наблюдения производится в векторно-матричной форме. На начальном этапе используется традиционная схема комплексной обработки информации измерителей с перекрестными связями, включающая в себя радиодальномер и МЭМС для измерения скорости [7] (рис. 2).
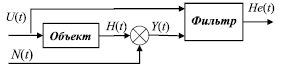
Рис. 1. Структурная схема комплексной обработки информации
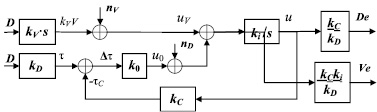
Рис. 2. Структурная схема комплексной обработки информации
На схеме обозначено: D – расстояние от подвижного объекта до цели; V – скорость подвижного объекта относительно цели; nD – флюктуационная помеха измерителя дальности; nV – погрешность измерителя скорости в виде цветного шума; De, Ve – оценки расстояния и скорости; kV, kD – коэффициенты пропорциональности соответственно измерителя скорости и дальности; ki – коэффициент интегратора; k0 – коэффициент усиления прямой цепи схемы слежения; kC – коэффициент обратной связи.
Представим схему преобразования сигналов в объекте наблюдения (рис. 2) в более подробном виде (рис. 3). На рис. 3 схема Obj1, обведенная пунктиром, включает объект (рис. 1) и формирователь измерений. Схема содержит: входной детерминированно-стохастический процесс D(t), состоящий из детерминированной составляющей mD(t) и случайной составляющей g(t); схему преобразования для входного сигнала скорости – WA(s), формирующий фильтр – WG(s) для сигнала g(t) и преобразователь П1. Для формирования измерений yV(t), yD(t) используется два сумматора.
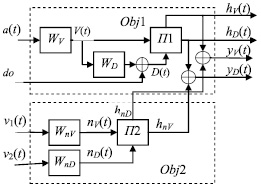
Рис. 3. Структурная схема объекта наблюдения
Объект Obj1 имеет два входа: a – сигнал ускорения, измеряемый микроакселерометром; do – начальное расстояние до цели и четыре выхода: hV(t) – скорость подвижного объекта; hD(t) – дальность до цели; yV(t) – измерение скорости; yD(t) – измерение дальности.
Анализ схем рис. 2 и 3 дает возможность определить уравнения преобразования объекта по выходам. Ускорение подвижного объекта a(t) определяет связанные с ним параметры движения – скорость и расстояние. Ускорение в данной задаче имеет некоторую постоянную составляющую – ao. Скорость движения объекта наблюдения в направлении цели связана с ускорением интегральным соотношением, расстояние определяется скоростью и начальной дальностью. Соответствующие дифференциальные уравнения и уравнение выхода имеют вид
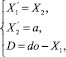 (1)
(1)
где в качестве компонент вектора состояния X обозначено: X1 – интеграл от скорости (приращение расстояния); X2 = V – скорость; D – расстояние.
Функции преобразования П1 рассматриваются на основе схемы рис. 2, где показано перекрестное преобразование скорости V и дальности D в сигнал u. Преобразование осуществляется с помощью следующего дифференциального уравнения (в переменных состояния u = X3).
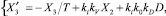 (2)
(2)
где T – постоянная времени (T рассчитана в статье [7] и составляет
T = (ki·k0·kC)–1,
где ki, k0, kC – коэффициенты схемы рис. 2).
Выходные сигналы hV и hD, согласно схеме рис. 2 и с учетом (2), вычисляются в виде
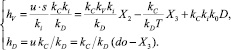 (3)
(3)
Таким образом, математическая модель объекта Obj1 определяется уравнениями (2), (3), (4), (7). Объединяя эти уравнения, получим систему
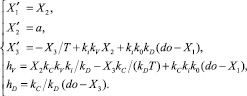 (4)
(4)
Для цветных шумов nV(t), nD(t), присутствующих на схеме рис. 3, необходимо также сделать представление их математических моделей в пространстве состояний. Схема преобразования формирующих шумов в выходные сигналы в виде приведенных к измерениям помех: hnV(t), hnD(t) на рис. 3 обозначена как Obj2. Так как измерительные шумы по скорости и дальности являются цветными, то для них требуются свои схемы формирования: WnV, WnD. Так же, как и в Obj1, требуется рассмотреть перекрестное преобразование шумов с помощью преобразователя П2. Для Obj2 формирующие шумы v2, v3 составляют вектор входа, а результаты: hnV(t), hnD(t) – вектор выхода. Исходные данные по характеристикам помех: nv(t), nD(t) представлены в материалах статьи [7] – это функции: SnD(ω) = σnD2ω2/(ω2 + αnD2); SnV(ω) = σnV2/(ω2 + αnV2), где обозначено соответственно для помех nV(t), nD(t): SnV, SnD – спектральные функции; σnV, σnD – среднеквадратические отклонения; αnV, αnD, – постоянные, характеризующие автокорреляцию.
Передаточные функции формирующих фильтров WnV, WnD получаются на основе исходных данных соответствующих спектральных функций SnV, SnD. Проводя факторизацию спектральных функций, получим WnD(s) = σnD·s/(s + αnD); WnV(s) = σnV/(s + αnV). Соответствующие дифференциальные уравнения формирующих фильтров имеют вид
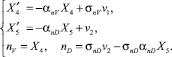 (5)
(5)
Функции преобразования П2 рассматриваются на основе схемы рис. 2, где показано перекрестное преобразование шумов nV(t), nD(t) в сигнал u. Преобразование осуществляется с помощью следующего дифференциального уравнения (в переменных состояния u = X6).
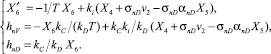 (6)
(6)
Измерения формируются в виде yV = hV + hnV – измерение скорости; yD = hD + hnD – измерение дальности:
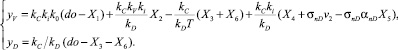 (7)
(7)
Математическая модель объекта для применения фильтра Калмана с целью комплексной обработки информации должна быть составлена в традиционной матричной форме: X’ = AX + Bu, Y = CX + Du. Объединяя системы уравнений (4)–(7), получим эту модель в виде большой системы из шести дифференциальных уравнений относительно четырех входов и четырех выходов. Из этой системы уже легко записать матрицы преобразований A, B, C, D:
A = [0,1,0,0,0,0;0,0,0,0,0,0;–ki*ko*kd,ki*kv, –1/T,0,0,0;0,0,0, –anv,0,0;0,0,0,0, –and,0;0,0,0,ki, –ki*snd*and,–1/T];
B = [0,0,0,0;1,0,0,0;0,ki*ko*kd,0,0;0,0,snv,0;0,0,0,1;0,0,0,ki*snd];
C = [–kc*ko*ki,kc*kv*ki/kd,-kc/kd/T,0,0,0;0,0, –kc/kd,0,0,0;
–kc*ko*ki,kc*kv*ki/kd, –kc/kd/T,kc*ki/kd, –kc*ki*snd*and/kd, –kc/kd/T;0,0, –kc/kd,0,0, –kc/kd];
D = [0,kc*ko*ki,0,0;0,kc/kd,0,0;0,kc*ko*ki,0,kc*ki*snd/kd;0,kc/kd,0,0].
Пример моделирования комплексной измерительной системы
Моделирование комплексной системы выполняется в Matlab. Программа моделирования имеет управляющую часть и программу-функцию. Исходные данные по конкретным параметрам спектральных функций помех, измеряемому ускорению, начальной дальности задаются в управляющей программе. Их конкретные значения следующие: Ta = 1e – 3; T = 26.4; snd = 1e2; snv = 1e2; and = 15; anv = 11. Как следует из статьи [7], параметры kv и kC предварительно выбираются из условия инвариантности: kC = kD, kV = 1/ki, их конкретные значения в этом случае составляют: ki = 0,0042; kv = 237,8; kc = 3,0e-6; kd = 3e-6; ko = 3e + 6. В управляющей программе использован вызов программы-функции, которая осуществляет расчет полной матричной модели, расчет фильтра Калмана и производит симуляцию их работы во времени.
В результате моделирования получены численные и графические результаты выходных сигналов подвижного объекта hv и hd, выходных оценок с фильтра Калмана hve и hde и численные оценки ошибок (средних квадратов). Полученные значения СКО дают максимальную величину ошибки оценивания, как 3σ: по дальности – 0,1 м, по скорости – 0,07 м/с, что на 10 % лучше, чем приведено в статье [7].
Выводы
Алгоритм обработки информации, поступающей с радиодальномера и МЭМС акселерометра, работает на основе принципов инвариантности. Комплексная обработка информации осуществляется при наличии перекрестных связей. Математическая модель объекта наблюдения составлена в векторно-матричной форме с целью применения фильтра Калмана для борьбы с помехами.
В результате компьютерного моделирования получены оценки эффективности комплексной системы в условиях помех. Полученные результаты доказывают эффективность применения комплексной обработки информации при различной интенсивности помех, как для быстрых, так и для медленных измеряемых процессов. Однако для настройки фильтра Калмана в этом случае приходится проводить дополнительную идентификацию мощности помехи и сигнала.
Прикладным результатом исследования является применение предложенной методики построения математических моделей и алгоритмов оценивания фазового состояния в системах определения пространственного положения маневренных подвижных объектов в широком диапазоне сигналов и помех. Новизна исследований проявляется в обеспечении эффективности комплексной системы обработки информации в условиях случайной среды. Предложенные алгоритмы комплексной обработкой информации при счислении координат маневренного объекта позволяют повысить точность измерительной системы.
Рецензенты:Вавилов В.Д., д.т.н., профессор кафедры «Авиационные приборы и устройства», ФГБОУ ВПО НГТУ, Арзамасский политехнический институт (филиал), г. Арзамас;
Ямпурин Н.П., д.т.н., профессор кафедры «Конструирование и технология радиоэлектронных средств», ФГБОУ ВПО НГТУ, Арзамасский политехнический институт (филиал), г. Арзамас.
Работа поступила в редакцию 27.12.2014.
Библиографическая ссылка
Жидкова Н.В., Волков В.Л. ЭФФЕКТИВНОСТЬ КОМПЛЕКСНОЙ ИЗМЕРИТЕЛЬНОЙ СИСТЕМЫ В УСЛОВИЯХ СЛУЧАЙНОЙ СРЕДЫ // Фундаментальные исследования. 2014. № 12-7. С. 1394-1399;URL: https://fundamental-research.ru/ru/article/view?id=36374 (дата обращения: 17.11.2025).



