Надёжность и энергетическая эффективность работы ядерных энергетических установок – реакторов и тепловых электрических станций обеспечивается, в частности, оптимальным режимом работы теплообменных устройств, таким, чтобы теплопередача от каждого нагретого элемента к теплоносителю была наибольшей при исключении возможности превышения максимально допустимой температуры поверхности их. Такой режим работы теплообменников может достигаться при правильном расположении поверхностей нагрева или тепловыделяющих элементов в сборке, а также и оптимальным выбором профиля скорости теплоносителя на входе в сборку, влияние на который оказывают геометрические и гидродинамические параметры входного устройства.
Из рассмотрения известных работ по исследованию гидродинамики теплоносителя во входных коллекторах теплообменников видно, что существует множество конструктивных вариантов выполнения таких коллекторов. При этом ставится практически единственная цель – получить заданный закон распределения потока по трубной доске или решетке при наименьшем гидравлическом сопротивлении в коллекторе. В большинстве случаев этот закон – равномерное распределение.
Подбор конструктивных элементов натурального теплообменника для обеспечения заданного распределения потока теплоносителя часто трудно выполним и ограничивается изменением одного какого-либо параметра, поэтому необходимо заранее знать, как повлияют те или иные изменения во входном коллекторе на поток теплоносителя.
Целью настоящей работы являлось экспериментальное комплексное многопараметрическое исследование влияния входных возмущений: неравномерности подвода теплоносителя, геометрии днища, закрутки потока на входе в коллектор и гидравлического сопротивления коллектора на поле скоростей на выходе из входного коллектора теплообменника.
На рис. 1 представлена схема экспериментальной модели входного цилиндрического раздаточного коллектора теплообменника.
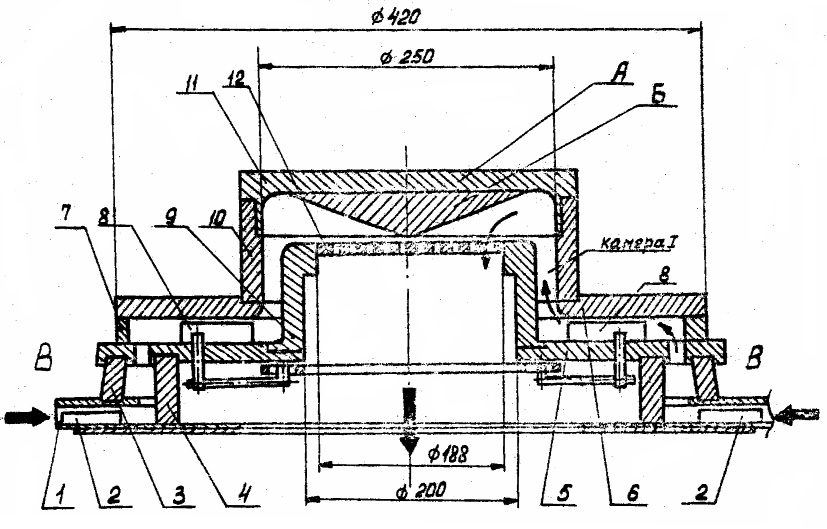
Рис. 1. Общий вид модели входного устройства:
1 – диффузор; 2 – лопатки; 3, 4 – обечайки; 5, 6 – фланцы; 7 – проставочное кольцо;
8 – лопатки; 9, 10 – обечайки; 11, А – крышка;
12 – перфорированная решётка; Б – сменная вставка
Вход в исследуемое входное устройство представляет собой восемь патрубков, равномерно распределённых по окружности, переходящих в диффузоры 1. Изменяя расход воздуха в патрубках, можно изменять распределение скоростей на входе в устройство. В каждом из диффузоров расположены четыре лопатки 2, служащие для выравнивания потока. Лопатки имеют поперечные прорези, что позволяет закрепить их на основании устройства и диффузора и, перемещая их по длине прорези, менять распределение потока.
Пройдя диффузоры, воздух поступает в зазоры между двумя обечайками 3 и 4 конфузорного сечения. Далее воздух поступает в кольцевой зазор, образованный двумя фланцами 5 и 6 и проставочным кольцом 7. В этом зазоре по ходу воздуха расположены 48 лопаток 8, которые позволяют закручивать поток воздуха от 0 до 30 градусов. Далее воздух поступает в кольцевой зазор между обечайками 9 и 10. Этот зазор имитирует кольцевую щель реактора. Величина зазора может изменяться путём изменения наружного диаметра обечайки 9. Далее воздух, поворачивая на 90°, поступает в зазор между крышкой 11 и перфорированной решеткой 12, имитирующей входную напорную камеру. Величина зазора и форма камеры могут изменяться путём установки днищ различной конфигурации и кольцевых прокладок между крышкой 11 и обечайкой 10. Меняя перфорацию решетки 12, можно изменять величину гидравлического сопротивления на выходе из камеры. Пройдя решетку 12, воздух попадает в выравнивающую камеру – пространство между решетками, а затем выбрасывается на пневмозонд.
Основные узлы модели являются легко разбираемыми и заменяемыми, что позволяет легко и быстро изменять геометрические характеристики исследуемых камер и других элементов гидравлического тракта. Если, например, необходимо увеличить высоту камеры, то устанавливаются обечайки нужной высоты.
Пневмозонд, устанавливаемый на выходе из решетки 12, обеспечивает фиксацию одновременно 36 значений динамических давлений в потоке и может поворачиваться с шагом 5° в плоскости, перпендикулярной потоку, давая возможность получать мгновенные радиальные и тангенциальные распределения скоростей потока и, кроме того, его можно устанавливать как непосредственно вплотную к решётке, так и смещать вдоль потока в диапазоне (0–0,2) м
от решётки.
Таким образом, экспериментальная модель позволяет получать двумерные распределения скорости потока на выходе из входного устройства при возмущениях различного вида на входе во входное устройство: несимметричный поток на входе, величину закрутки потока, высоту напорной камеры, форму днища напорной камеры, величину гидравлического сопротивления на выходе из входного устройства.
При проектировании круговых раздаточных коллекторов парогенераторов решается, в частности, задача достижения устойчивости поля скоростей на выходе коллектора при известных ограничениях на гидравлическое сопротивление направляющей решетки [1, 3, 4, 5]. В связи с этим представляют интерес аналитические зависимости для определения поля скоростей теплоносителя на выходе из решётки раздаточного коллектора, учитывающей геометрические параметры коллектора. Целью работы здесь является разработка методики перехода от дискретного оттока из решётки коллектора к непрерывному и построение математической модели, описывающей распределение расхода на выходе из коллектора, как с дискретным – непосредственно вблизи решётки, так и непрерывным оттоком – на удалении от неё.
Уравнение регрессии определялось на основе массива экспериментальных данных о полях скоростей на выходе из модели кругового раздаточного коллектора теплообменника с различными соотношениями высоты входной камеры к её диаметру и различными гидравлическими сопротивлениями решетки на выходе из камеры. Эксперименты проводились на модели кругового раздаточного коллектора, позволяющей изменять эти параметры. Относительная погрешность измерений полей скоростей потока составляет в среднем 
при максимальной погрешности σmax(V) = 3,3 %.
Зависимость скорости теплоносителя от радиуса на выходе из коллектора представляется в виде
(1)
где I – максимальная степень полинома аппроксимации, который определяется методом наименьших квадратов (МНК) по всему массиву экспериментальных данных; αj – коэффициенты, вычисляемые МНК с использованием экспериментальных данных для конкретного набора геометрических параметров коллектора; r – текущий радиус.
Нормировка
(2)
где 
– среднерасходная скорость через решетку коллектора.
Из (1) и (2) относительная скорость теплоносителя на выходе из коллектора:
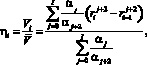(3)
где Vi – средняя скорость теплоносителя между радиусами ri и ri–1.
Как показывают экспериментальные данные, на выходную гидравлическую неравномерность оказывают влияние следующие факторы: геометрические размеры камеры (высота Н и диаметр D), коэффициент гидравлического сопротивления ξp, неравномерность входного профиля скоростей, наличие вихреобразования и др.).
Поскольку во все расчётные формулы оценки гидравлической неравномерности скорости ηi входит относительная высота коллектора 
и коэффициент гидравлического сопротивления решетки ξp, то необходимо учесть эти факторы.
Поэтому поле скоростей ищется в виде
(4)
где μ = 0;1; S = 0; 1; 2; p = 0; 1; ∞.
При равномерном подводе теплоносителя в коллектор модель удовлетворяет следующим физическим условиям:
для любых ξp, r;
для любых h, r.
Коэффициенты уравнения определялись методом пошаговой регрессии с помощью алгоритма Эфроимсона. В результате расчетов на ЭВМ была получена следующая аналитическая зависимость для коллектора, в котором 
(отсутствие стенок, ограничивающих поток):
(5)
Для коллектора, в котором 
(стенки ограничивают поток теплоносителя):
(6)
Коэффициент детерминации модели более 0,95.
По приведенной методике были выполнены расчеты для коллектора, гидродинамика которого исследовалась экспериментально [2]. Сопоставление показало, что максимальное расхождение расчетных и экспериментальных результатов составляет около 6 %. Приведённая в работе математическая модель (1)–(4) позволяет рассчитать распределения относительных скоростей на выходе из цилиндрического раздаточного коллектора только от его геометрических параметров H, D и гидравлического сопротивления ξp с точностью до 6 %.
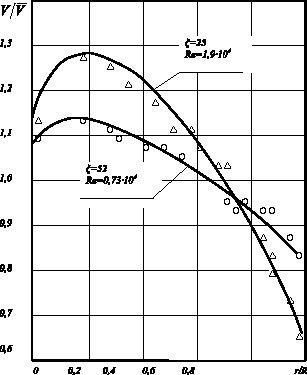
Рис. 2. Распределение относительных скоростей на выходе из раздаточного коллектора с трубным пучком (Н/D = 0,025):
, 
– эксперимент; 
– расчет по зависимости (6)
Примеры расчетов и сопоставление с экспериментом представлены на рис. 2, 3. Видна достаточно удовлетворительная сходимость расчета и эксперимента.
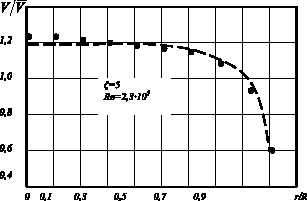
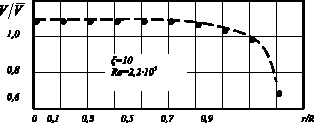
Рис. 3. Распределение относительных скоростей на выходе из раздаточного коллектора
с плоским дном и мелкоячеистыми сетками (Н/D = 0,1):
– эксперимент; 
– расчет по зависимости (5)
Запорожец Е.П., д.т.н., профессор кафедры «Нефтегазовый промысел им. профессора Г.Т. Вартумяна», институт нефти, газа и энергетики, Кубанский государственный технологический университет, г. Краснодар;
Кунина П.С., д.т.н., профессор, зав. кафедрой «Оборудование нефтяных и газовых промыслов», институт нефти, газа и энергетики, Кубанский государственный технологический университет, г. Краснодар.
Работа поступила в редакцию 19.12.2014.
Библиографическая ссылка
Дубоносов А.Ю., Гапоненко А.М., Даценко Е.Н. ЭКСПЕРИМЕНТАЛЬНОЕ ИССЛЕДОВАНИЕ И ПОЛИНОМИАЛЬНАЯ АППРОКСИМАЦИЯ ПОЛЕЙ СКОРОСТИ ТЕПЛОНОСИТЕЛЯ НА ВЫХОДЕ ИЗ МОДЕЛИ КРУГОВЫХ РАЗДАТОЧНЫХ КОЛЛЕКТОРОВ ТЕПЛООБМЕННОГО ОБОРУДОВАНИЯ ТЕПЛОВЫХ ЭЛЕКТРОСТАНЦИЙ И ЯДЕРНЫХ РЕАКТОРОВ // Фундаментальные исследования. – 2014. – № 12-6. – С. 1162-1166;URL: https://fundamental-research.ru/ru/article/view?id=36293 (дата обращения: 19.04.2024).