В ряде работ [1, 2, 3, 4], посвященных влиянию вариабельности на работу сбалансированной производственной системы, выявлена интересная особенность – изменение уровня запасов между операциями. Причем в процессе изменения уровня запасов кроме случайной составляющей наблюдается неслучайная составляющая, имеющая периодический характер. В ряде реализаций таких процессов, кроме периодической составляющей, можно выделить возрастающую линию тренда [3, 4]. По результатам моделирования работы сбалансированной производственной линии в условиях вариабельности делается предположение о том, что возрастание запасов будет происходить до уровня, когда запасы между производственными ячейками сделают их работу независимой друг от друга [1].
Для детального анализа причин изменения уровня запасов в сбалансированных производственных системах рассмотрим работу изолированной производственной ячейки на имитационной модели. Производственная ячейка состоит из двух элементов – запаса заготовок и станка.
В имитационной модели процесс обработки деталей производственной ячейки рассматривается как дискретная последовательность, длительность каждого шага которой равна одной рабочей смене. Работа производственной ячейки подчиняется следующим правилам:
● На вход производственной ячейки поступает случайный дискретный поток партий заготовок.
● Заготовки складируются перед станком.
● В течение смены оператор забирает заготовки из места хранения на обработку.
● Производительность станка является дискретной случайной величиной.
● Результатом работы производственной ячейки на каждом шаге является партия деталей, размер которой зависит от количества заготовок в месте хранения производственной ячейки и производительности станка.
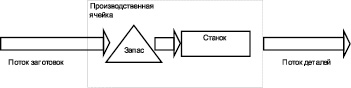
Рис. 1. Модель производственной ячейки
Для описания работы производственной ячейки введем следующие переменные:
V1i – количество заготовок, поступающих на обработку i-й смены;
V2i – производительность станка – количество единиц деталей, которое может обработать станок в течение i-й смены;
V3i – выпуск деталей – количество единиц деталей, которое обработано производственной ячейкой в течение i-й смены;
Qi–1 – запас заготовок перед станком в конце предыдущей (i – 1) смены;
Qi – запас заготовок перед станком в конце i-й смены.
Работа производственной ячейки описывается уравнением потоков и зависит от соотношения количества поступающих на обработку заготовок, остатка запаса заготовок от предыдущей смены и производительности станка. Запас заготовок производственной ячейки описывается следующей системой уравнений:
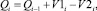
если 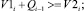
Qi = 0, если 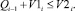 (1)
(1)
Выпуск деталей определяется следующими уравнениями выходного потока деталей:
 если
если 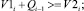
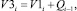 если
если 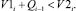 (2)
(2)
Уравнения показывают, что если сумма поступления заготовок и запас заготовок в производственной ячейке меньше производительности станка, то выпуск деталей оказывается меньше производительности станка, а запас снижается до 0.
Входной поток заготовок V1i и производительность оборудования V2i моделируются выборками из генеральной совокупности случайных чисел, имеющими равномерное дискретное распределение в диапазоне от 1 до 6. Использование данного распределения обеспечивает среднее значение набора случайных чисел, равное 3,5, а среднее квадратичное отклонение – 1,87. Использование одинаковых параметров наборов случайных чисел выбрано для обеспечения основного условия моделирования – обеспечения сбалансированности производственной ячейки.
Произведены расчеты имитационной модели производственной ячейки в среде Microsoft Office Excel. Входной поток заготовок и производительность станка моделировались наборами случайных чисел, которые были получены с помощью функции «Генерация случайных чисел» Пакета анализа Microsoft Office Excel. Объем наборов был принят равным 300 числам, что соответствует работе производственной ячейки в течение одного года. Начальное значение запаса производственной ячейки было принято равным 4 единицам. Одна из реализаций работы имитационной модели производственной системы представлена на рис. 2. На графике изменения объема запаса производственной ячейки можно выделить как случайные колебания объема запаса, так и неслучайные периодические изменения. В данной реализации объем запаса заготовок изменялся в диапазоне от 0 до 33. Полученные результаты имитационного моделирования качественно соответствуют результатам, приведенным в опубликованных работах [1, 2].
Анализ модели работы производственной ячейки позволяет сделать вывод, что функционирование производственной системы основано на простом уравнении потоков и не содержит обратных связей. Следовательно, причиной периодических изменений запасов заготовок может быть соотношение между поступлением заготовок на вход производственной ячейки и выходом готовых деталей.
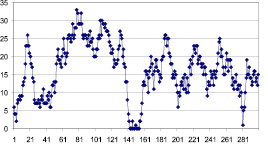
Рис. 2. Пример изменения уровня запаса в производственной ячейке
Для проверки этого предположения проведен анализ разностей между средними значениями входного и выходного потоков. Для получения данных о распределении средних значений в различных выборках, полученных при генерации случайных чисел, проведена генерация 100 наборов 300 случайных чисел в каждом наборе для равномерного распределения, имеющее среднее значение 3,5 и равную вероятность 0,1667 для чисел от 1 до 6.
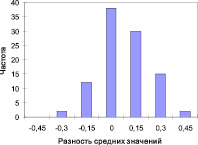
Рис. 3. Плотность распределения разности средних значений двух выборок
Так как при моделировании работы производственной ячейки используются два набора случайных чисел, то были вычислены разности между средними значениями двух соседних наборов. Были получены следующие данные:
■ Разности между средними значениями располагаются в диапазоне от –0,373 до +0,350;
■ Среднее значение по всем наборам составило 3,4913, что близко к теоретическому значению, равному 3,5.
Плотность распределения разностей средних значений представлена на рис. 3. Результат моделирования наборов случайных чисел наглядно свидетельствует, что средние значения наборов являются случайной величиной и в рассматриваемом случае имеют стандартное отклонение равное 0,142.
При моделировании работы изолированной производственной ячейки используются два набора случайных чисел, один из которых определяет поступление заготовок, а второй – производительность станка. Строгое соблюдение условия сбалансированности производственной ячейки будет выполняться только в том случае, когда оба набора случайных чисел будут иметь равные средние значения. Однако при имитационном моделировании работы производственной ячейки возможно соблюдение условия сбалансированности только в пределах разброса средних значений совокупности выборок, используемых для входного потока заготовок и производительности оборудования. Будем считать, что такой разброс будет меньше, чем разброс средних значений в реальных сбалансированных производственных системах.
Анализ формулы расчета запаса (1) показывает, что одним из параметров, влияющих на запас заготовок, является разность скоростей на входе в производственную ячейку и производительности оборудования. Поэтому для обработки данных имитационного моделирования были использованы следующие параметры:
dV = V1 – V2 – разность потоков (разность между поступлением заготовок и производительностью станка);
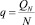 – приведенный запас, где QN значение запаса в конце испытания, N – количество смен при моделировании. Параметр приведенного запаса введен для приведения размерности запаса Q к размерности переменных, обозначающих параметры потока V.
– приведенный запас, где QN значение запаса в конце испытания, N – количество смен при моделировании. Параметр приведенного запаса введен для приведения размерности запаса Q к размерности переменных, обозначающих параметры потока V.
Было проведено 11 сеансов имитационного моделирования, в которых использовались наборы случайных чисел, полученные для анализа закона распределения средних значений. Результаты имитационного моделирования сбалансированной производственной ячейки приведены в таблице и на рис. 4. Символ ● использован для отображения данных моделирования, при которых dV <= 0, а символ ■ – для отображения данных моделирования, при которых dV >= 0. Такое разделение данных соответствует двум режимам работы производственной ячейки – при положительной и отрицательной разности потоков dV.
Анализ полученных данных подтверждает предположение о том, что зависимость приведенного запаса q от разности потоков dV определяется знаком разности dV. При отрицательном значении разности потоков dV угол наклона уравнения регрессии равен 0,084. Если разность потоков dV положительна, что соответствует случаю, когда на производственную систему поступает заготовок больше, чем производительность оборудования, то угол наклона уравнения регрессии равен 0,552.
Данные моделирования производственной ячейки
|
Номер сеанса |
Разность потоков (dV) |
Приведенный запас (q) |
Символы |
|
1 |
–0,523 |
0,011 |
● |
|
2 |
–0,307 |
0,023 |
● |
|
3 |
–0,230 |
0,026 |
● |
|
4 |
–0,007 |
0,053 |
● |
|
5 |
0,000 |
0,054 |
● ■ |
|
6 |
0,153 |
0,087 |
■ |
|
7 |
0,170 |
0,100 |
■ |
|
8 |
0,230 |
0,210 |
■ |
|
9 |
0,307 |
0,153 |
■ |
|
10 |
0,387 |
0,257 |
■ |
|
11 |
0,523 |
0,331 |
■ |
Структура уравнения пополнения запасов (1) позволяет разности Qi – Qi–1 поставить в соответствие приведенный запас q. Тогда можно уравнение (1) записать в следующем виде:
q = dV. (3)
На графике (рис. 4) видно, что уравнение (3) качественно соответствует уравнению регрессии при dV > 0.
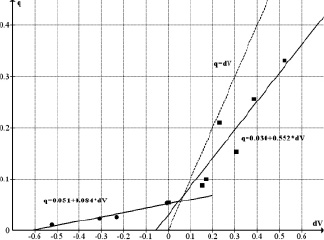
Рис. 4. Зависимость приведенного запаса q от разницы потоков dV
Анализ результатов имитационного моделирования сбалансированной производственной ячейки позволяет сделать следующие выводы:
● Работа сбалансированной производственной ячейки существенно зависит от среднего значения случайного входного потока заготовок и среднего значения случайной производительности оборудования.
● В том случае, когда среднее количество поступления запасов меньше среднего значения производительности станка, возрастание запасов минимально.
● В том случае, когда среднее количество поступления запасов больше среднего значения производительности станка, происходит возрастание запасов в производственной ячейке прямо пропорционально разности средних значений.
Полученные выводы подтверждают графики изменения запасов для двух режимов работы производственной ячейки.
Анализ графиков (рис. 5, 6) позволяет сделать вывод, что нарастание запасов наблюдается как при отрицательной, так и при положительной разности скоростей dV. Если нарастание запаса при положительной разнице между поступлением заготовок и производительностью оборудования является очевидным, то нарастание запасов при отрицательной разнице этих величин требует дополнительного изучения.
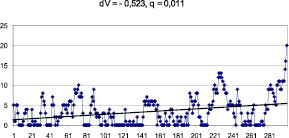
Рис. 5. График изменения запасов производственной ячейки при отрицательной величине разности поступления запасов и производительности оборудования
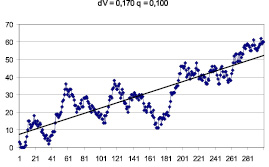
Рис. 6. График изменения запасов производственной ячейки при положительной величине разности поступления запасов и производительности оборудования
Рассмотрим процесс изменения разности поступления заготовок и производительности оборудования (разность потоков) dV для случая, когда среднее значение разности имеет отрицательное значение.
Анализ данных изменения запаса и разности между поступлением заготовок и производительностью оборудования показывает (рис. 7), что в реализации случайного процесса разности потоков dV можно наблюдать выбросы случайного процесса [3] – пересечение процесса заданного уровня. В рассматриваемом случае процессом является изменение dV, а уровнем является нулевое значение dV. Положительные выбросы этого процесса интегрируются, что приводит к нарастанию запаса. Отрицательные выбросы снижают запасы до нулевого уровня, но не могут сделать его отрицательным. Такая особенность объясняется односторонней проводимостью производственной ячейки, так как она может перемещать поток только от входа к выходу. В итоге перед станком образуется запас заготовок, объем которого зависит от величины разности поступления заготовок и производительности станка.
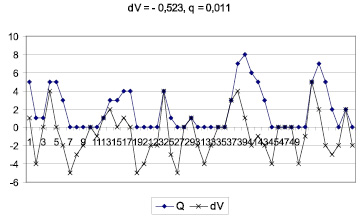
Рис. 7. Работа производственной ячейки при отрицательной разности скоростей dV
Заключение
При проведении имитационного моделирования производственных систем необходимо контролировать соотношение средних значений выборок случайных чисел, используемых для моделирования отдельных элементов производственной системы, так как разность этих средних значений может оказывать значительное влияние на результаты моделирования.
Рецензенты:Панов А.Ю., д.т.н., заведующий кафедрой «Теоретическая и прикладная механика», ФГБОУ ВПО «Нижегородский государственный технический университет им. Р.Е. Алексеева», г. Нижний Новгород;
Кретинин О.В., д.т.н., профессор кафедры «Автоматизация машиностроения», ФГБОУ ВПО «Нижегородский государственный технический университет им. Р.Е. Алексеева», г. Нижний Новгород.
Работа поступила в редакцию 16.12.2014.
Библиографическая ссылка
Запорожцев А.В. АНАЛИЗ ПРИЧИН ИЗМЕНЕНИЯ УРОВНЯ ЗАПАСОВ В СБАЛАНСИРОВАННОЙ ПРОИЗВОДСТВЕННОЙ ЯЧЕЙКЕ // Фундаментальные исследования. 2014. № 12-4. С. 717-722;URL: https://fundamental-research.ru/ru/article/view?id=36176 (дата обращения: 19.12.2025).



