Постановка задачи. Рассмотрим линейное дифференциальное уравнение второго порядка с частными про-
изводными
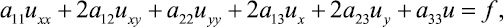(1)
где коэффициенты aij и f являются функциями переменных x и y, причем точка (x, y) принадлежит общей области G определения всех функций, входящих в уравнение (1), в том числе и неизвестной функции u(x, y). Граничные условия не участвуют при решении поставленной ниже задачи, поэтому тип граничной задачи оговорен не будет.
Сформулируем задачу данной работы:
указать последовательность невырожденных преобразований независимых переменных, в результате реализации которой главная часть уравнения (1) примет вид суммы вторых производных с равными коэффициентами, а коэффициент при смешанной производной будет равен нулю.
Изначально предполагаем, что уравнение (1) в G есть уравнение эллиптического типа, т.е.
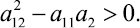(2)
В некоторых учебных пособиях (см. [1]) при преобразовании уравнения эллиптического типа вначале идут по тому же пути, что и в случае гиперболического уравнения (приводят главную часть к виду, содержащему только смешанную производную), а затем преобразованием, в котором выделяются действительная и мнимая части у последних переменных, уравнение эллиптического типа записывается в требуемом виде. Однако подобный эксперимент не применим при решении научных задач [2, 6].
Однако такое преобразование содержит ошибочное утверждение о комплексной сопряженности переменных, которые определяются из общих интегралов для комплексных характеристических уравнений. Ошибочность утверждения состоит в том, что характеристические уравнения в комплексной области не являются комплексно-сопряженными, и поэтому соответствующие им общие интегралы также таковыми не являются.
Первый этап преобразования. В связи с тем, что сокращение числа членов в главной части уравнения эллиптического типа может быть сделано единственным образом, а именно только избавлением слагаемого со смешанной производной, зададимся целью достичь этого за счет выбора соответствующего преобразования. Пусть задано преобразование вида
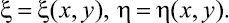(3)
В результате этого преобразования коэффициент A12 перед смешанной производной uξη примет вид
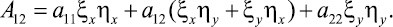(4)
Запишем равенство (4) в следующем виде, приравняв нулю коэффициент A12,
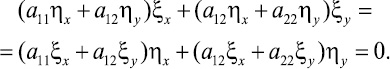(5)
Так как для отыскания замены переменных (3) возникает только одно уравнение (5), то имеющийся произвол можно устранить, рассмотрев один из четырех вариантов:
1) 
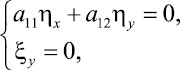
2) 
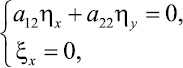(6)
3) 
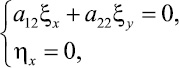
4) 
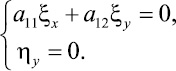
Возможны ещё два варианта приравнивания к нулю сомножителей в равенстве (5), но один из них ξx = ξy = 0 или ηx = ηy = 0 приводит к тому, что либо ξ = const, либо η = const. Этого не может быть, так как ξ и η в новых переменных являются аргументами функции u(ξ, η), область определения которой выродилась бы в одномерную область ξ = const или η = const, что может быть только при вырожденном отображении области D. Второй вариант, когда
1) 
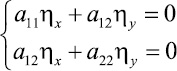
или
2) 
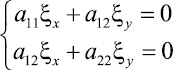
в силу неравенства нулю определителя этой системы
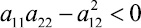
приведет к ηx = ηy = 0, либо ξx = ξy = 0. Тем самым возникает ситуация из предыдущего варианта.
В каждом из этих вариантов одна из «новых» переменных связана только с одной из «старых» переменных. Следует отметить, что варианты 1 и 4 по существу совпадают. Точно также совпадают варианты 2 и 3. Отличие состоит только в обмене ролями между переменными ξ и η, или, что то же самое, в замене обозначений для новых переменных.
Изучению подлежит лишь случай, когда все три коэффициента a11, a12 и a22, не обращаются в нуль. Поэтому можно остановиться на первом случае
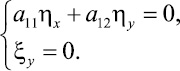(7)
Из второго уравнения следует, что ξ = ξ(x).
В связи с уравнением
a11 ηx + a12 ηy = 0 (8)
справедлива следующая теорема.
Теорема. Для того чтобы функция η = η(x, y) была решением уравнения (8) в области D, необходимо и достаточно, чтобы соотношение
η(x, y) = C (9)
в области D определяло общий интеграл уравнения
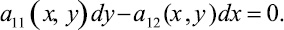
Таким образом, функция η(x, y), стоящая в правой части интеграла (9), является решением уравнения в частных производных (5), а замена переменных ξ = ξ(x), η = η(x, y) обращает в нуль в преобразованном уравнении (4) коэффициент A12 = 0. Если выбрать произвольную функцию ξ(x) такой, что ξx ≠ 0 ни в одной точке области D, то для невырожденности предлагаемого преобразования переменных из якобиан преобразования
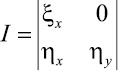
следует, что ηy ≠ 0. Это условие естественно, т.к. ξ зависит только от x, то вторая переменная η обязана зависеть от y.
В предлагаемой замене переменных имеется определённый произвол: ξ(x) – произвольная функция, и хотя η(x, y) = C – интеграл уравнения (8), но достаточно гладкая функция f(η(x, y)) = C также является интегралом. Поэтому поставим задачу:
одновременно с равенством A12 = 0 подобрать ξ = ξ(x) и η = η(x, y) так, чтобы выполнялось ещё одно равенство
A11 = A22, (10)
которое обеспечит следующий вид глав-
ной части:
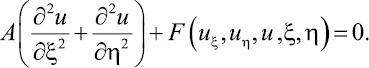(11)
Предварительно преобразуем равенство (10) с учётом того, что равенство A12 = 0 получено при условиях (7):
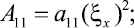
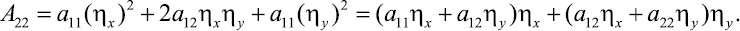
Так как в силу уравнения (8) первая скобка равна нулю, то
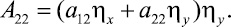
Тогда равенство (10) можно записать в следующем виде:
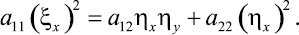
С учетом невырожденности проводимого преобразования можно поделить это равенство на (ηy)2 ≠ 0 и в результате получить
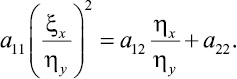
Найдём отношение ηx/ηy из соотношения (8) и его подставим в последнее равенство
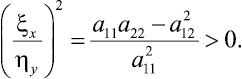
Таким образом, равенство возможно. Для того чтобы из него можно было определить ξx, необходимо и достаточно, чтобы в равенстве
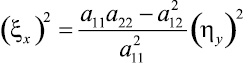, (12)
и его правая часть зависела только от x. Выполнение этого условия позволит определить функцию ξ = ξ(x) вместе с функцией η = η(x, y), найденной из уравнения a12ηx + a12ηy = 0. Эти две функции зададут преобразование, с помощью которого уравнение (1) будет иметь вид (11), называемый каноническим для уравнения эллиптического типа. Если же с помощью равенства (11) в силу того, что его правая часть не будет удовлетворять необходимому условию и потому нельзя будет определить ξx, то для приведения уравнения эллиптического типа к каноническому виду можно использовать вторую возможность, решив систему
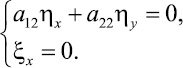(13)
Тогда необходимым и достаточным условием приведения к каноническому виду уравнения (1) будет условие
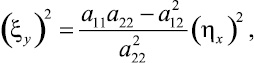(14)
где правая часть должна зависеть только от y. Проверка условий (12) или (14) возможна только после решения соответственно уравнений a11ηx + a12ηy = 0 или a12ηx + a22ηy = 0, вместо которых согласно теореме можно использовать общий интеграл одного из характеристических уравнений,
a11dy – a12dx = 0
или
a12dy – a22dx = 0 (15)
Вывод
При интегрировании уравнений (12) или (14) требование зависимости только от одной переменной не является обязательным, т.к. из интегралов соответствующих характеристических уравнений можно выразить одну из переменных через другую и затем из правых частей уравнений (12) или (14) ненужную переменную исключить. В результате получим зависимость только от одной переменной, по которой слева в уравнении (12) или (14) осуществляется дифференцирование.
Замечание. Результаты работы докладывались на конференциях [4, 5, 7] и получили одобрение их участников.
Рецензенты:Тедеев А.Ф., д.ф.-м.н., заведующий отделом уравнений математической физики, ИПММ НАН Украины, г. Донецк;
Сухинов А.И., д.ф.-м.н., профессор, заведующий кафедрой МОСК, ФГАОУ ВПО «Южный федеральный университет»,
г. Таганрог.
Работа поступила в редакцию 28.11.2014.
Библиографическая ссылка
Илюхин А.А. НОВЫЙ АЛГОРИТМ ПРИВЕДЕНИЯ ДВУМЕРНОГО УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА К КАНОНИЧЕСКОМУ ВИДУ // Фундаментальные исследования. – 2014. – № 11-12. – С. 2636-2639;URL: https://fundamental-research.ru/ru/article/view?id=36036 (дата обращения: 19.04.2024).