Исполнительные системы составляют основу промышленных систем управления. К ним предъявляются повышенные требования, обусловленные, как правило, тяжелыми условиями эксплуатации, необходимостью обеспечения точного управления технологическими процессами и надежности. Характеристики и параметры систем зависят от свойств используемых материалов. В настоящее время возможности «традиционных» материалов во многом уже полностью реализованы. Однако разработаны и начинают широко использоваться «интеллектуальные» материалы, которые могут контролируемым образом преобразовывать один вид энергии в другой. К ним в полной мере относятся и ферромагнитные материалы с памятью формы (ФМПФ). Они обладают высокой чувствительностью и возможностью изменять геометрические размеры в широком диапазоне под воздействием магнитных и механических сил [2, 3]. Это позволяет упростить конструкцию исполнительных устройств, повысить точность преобразования, а также сократить количество составных частей, подверженных поломке или изнашиванию. Сложный характер происходящих в ФМПФ физических процессов и недостаточно развитая теоретическая база для проектирования приводят к тому, что значительные возможности этих материалов используются не в полной мере. Известны, как правило, опытные образцы устройств, изготовленных с применением ФМПФ [4, 5]. Анализ работ показывает, что проводятся испытания и определяются свойства отдельных образцов ФМПФ и, как правило, не учитывается их определяющее влияние на характеристики и параметры исполнительных систем. В этой связи разработка математических моделей для исследования и диагностирования исполнительных систем, построенных на основе ФМПФ, является актуальной задачей.
Цель работы: разработка математических моделей деформации активного элемента исполнительной системы на основе ФМПФ.
Материал и методы исследований: методы математического анализа, математического моделирования, численные методы интегрирования, численные методы решения алгебраических уравнений теории измерений.
Результаты исследований и их обсуждение
Предлагается исполнительная система, построенная с применением активного элемента (АЭ) из ФМПФ и распределенной намагничивающей катушкой, состоящей из ряда катушек малого размера. Используется режим импульсного перемагничивания АЭ с возможностью регулирования величины напряженности магнитного поля. АЭ, представляющий собой стержень в виде параллелепипеда, намагничивается неравномерно. Тем самым неэффективно используются возможности ФМПФ – изменение линейных размеров от воздействия магнитного поля. Поэтому для диагностики и управления процессами деформации АЭ предлагаются математические модели, учитывающие эти особенности.
Упрощенная схема линейного привода исполнительной системы показана на рис. 1, где 1 – недеформированный АЭ из ФМПФ, закрепленный на одном конце и управляемый магнитным полем, задаваемым токами в катушках 2. Устройство характеризуется следующими параметрами: N – число катушек, L0 – полная длина недеформированного АЭ, l – протяженность зоны действия магнитного поля, создаваемого катушкой, l ≪ L0. Протяженность зоны действия катушки связана с длиной АЭ следующим образом: l = κL0, κ < N–1. Неоднородностью магнитного поля в образце в зоне действия одной катушки пренебрегаем. Считается, что участки, деформированные воздействием магнитного поля какой-либо катушки, не заходят в область воздействия других катушек.
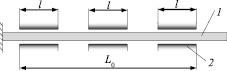
Рис. 1. Упрощенная схема линейного привода исполнительной системы
В рамках рассматриваемой модели предполагается, что деформация происходит следующим образом: за некоторый промежуток времени Δt области образца, подвергающиеся действию создаваемого катушками поля, удлиняются на максимально возможную величину. Удлинение каждой из областей при этом составит λl, где λ – максимальная относительная деформация АЭ под воздействием магнитного поля. Полная деформация за время Δt составит
 .
.
В результате описанной деформации в зону действия катушек заходят недеформированные участки АЭ (см. рис. 2). На следующем «такте», т.е. за очередной промежуток времени Δt, эти участки удлинятся на λ2l, 2λ2l, 3λ2l и т.д. Окончательное значение деформации находится суммированием соответствующих значений за все время деформации:
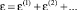
Выписав выражение для ε в явном виде
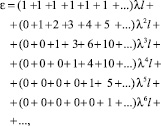
легко заметить, что коэффициенты при λkl представляют собой числа, составляющие треугольник Паскаля. Таким образом, величина деформации легко вычисляется для образца, управляемого любым количеством катушек.
Соотношение между деформациями на k-м и (k – 1)-м тактах равно λkl/λ(k –1) l = λ. Поэтому для рассматриваемых материалов предлагаемая модель позволяет повысить точность расчета приблизительно на 10 % по сравнению с расчетом, учитывающим только область АЭ в зоне действия катушек.
Погрешность описанной модели, возникающая вследствие того, что деформация до максимального значения происходит не мгновенно, большей частью компенсируется за счет того, что вошедшие в зоны действия катушек участки АЭ находятся в этих зонах на протяжении всей дальнейшей деформации и успевают деформироваться до максимума.
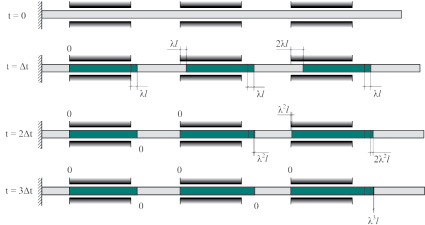
Рис. 2. Деформация активного элемента
После нескольких циклов работы АЭ в нем появляются остаточные деформации, учет которых требует усложнения модели. Относительная деформация на момент начала удлинения теперь не считается равной нулю во всем АЭ, а описывается функцией от координаты x (координата отсчитывается от места закрепления стержня). Для простоты будем считать, что эта функция λ(0) (x) принимает значения 0 и 1, отвечающие соответственно отсутствию деформации и полной деформации. Образец с остаточной деформацией изображен на рис. 3, деформированные участки заштрихованы.
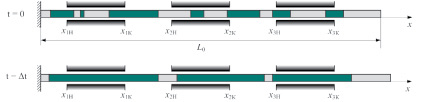
Рис. 3. АЭ с остаточной деформацией
Модель не требует ограничений на попадание участков, деформированных под воздействием одних катушек, в зоны влияния других. Деформация участка образца, попавшего под действие j-й катушки, на первом такте выражается следующей формулой:
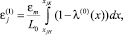
где εm – максимальная абсолютная деформация образца; xjH, xjK – границы зоны действия j-й катушки. После первого «такта» относительная деформация будет выражаться уже новой функцией λ(1) (x), которая будет исходной для нахождения удлинения на втором такте, и аналогично для последующих тактов. Таким образом, деформация, вызванная воздействием j-й катушки на k-м «такте», равна
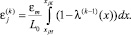 (1)
(1)
Неудобством такого метода является необходимость построения новой функции λ(k) (x) на каждом такте. Примем допущение: участки, деформированные после t = 0, за все время деформации не попадают в зоны действия катушек. При этом на каждом такте интегрирование в формулах (1) можно производить не по зоне действия катушек, а по участкам, попавшим в зоны действия на предыдущем такте. Тогда деформация на этих участках будет описываться функцией λ(0) (x) и для вычисления 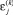 достаточно лишь соответствующим образом выбрать пределы интегрирования.
достаточно лишь соответствующим образом выбрать пределы интегрирования.
Дальнейшее уточнение модели деформации образца должно происходить путем учета вида зависимости деформации от приложенного магнитного поля H для конкретного материала АЭ, а также зависимости φ(x), описывающей распределение поля, создаваемого катушками в АЭ. В этом случае выражение (1) принимает вид
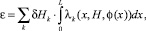
где λk(x, H, φ(x)) – функция, описывающая удельную деформацию АЭ на k-м шаге изменения магнитного поля; δHk – приращение магнитного поля на k-м шаге; L – область АЭ, в которой присутствует поле, создаваемое катушками. В общем случае поле присутствует во всем АЭ, и тогда L равно длине АЭ на k-м шаге изменения магнитного поля Lk.
Выполним моделирование деформации АЭ исполнительной системы под воздействием напряженности магнитного поля, создаваемого шестью катушками, с помощью предложенной модели.
Зависимость деформации от напряженности магнитного поля ε(H) аппроксимируем подобно тому, как это делается для магнитного гистерезиса у ферромагнетиков [1]. Для этого используем функции
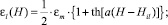 (2)
(2)
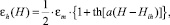 (3)
(3)
описывающие соответственно нижнюю и верхнюю ветви петли гистерезиса. В этих формулах εm – максимальная деформация; параметр a определяет крутизну петли гистерезиса; Hil и Hih – значения напряженности магнитного поля, соответствующие точкам перегиба нижней и верхней ветвей. Указанные параметры подбираются исходя из вида экспериментальной зависимости ε(H) для данного материала.
Распределение напряженности по длине АЭ в указанной системе по экспериментальным данным показано на рис. 4. Представим это распределение с помощью нормированной на единицу функции вида
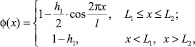
где l – расстояние между центрами катушек; h1 – параметр, характеризующий неоднородность поля (для рассматриваемой системы h1 составляет около 0,2), 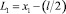 ,
, 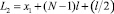 , N – число катушек (в рассматриваемом случае N = 6); x1 – координата центра первой катушки.
, N – число катушек (в рассматриваемом случае N = 6); x1 – координата центра первой катушки.
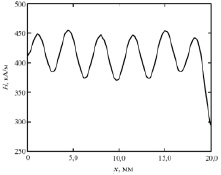
Рис. 4. Распределение напряженности магнитного поля в АЭ
Выражение для напряженности магнитного поля в АЭ в зависимости от координаты x получается умножением функции φ(x) на величину напряженности Hm в точках АЭ, соответствующих центрам катушек xk. Используя ту же аппроксимирующую функцию, что и для получения формул (2) и (3), получим для распределения удельной деформации по длине образца без начальной деформации после первого такта удлинения выражение
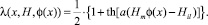
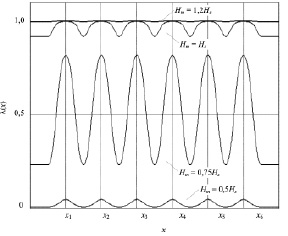
Рис. 5. Распределение удельной деформации λ(x) по длине АЭ
Графики зависимости удельной деформации от координаты xk при различных значениях Hm представлены на рис. 5. На рисунке Hs – напряженность насыщения магнитного поля АЭ.
Заключение
Предложены математические модели для определения деформации АЭ в условиях его неравномерного намагничивания. Применение моделей позволяет учитывать начальное состояние АЭ и его остаточную деформацию. Полученные результаты позволяют повысить точность определения параметров исполнительных систем на основе ферромагнитных материалов с памятью формы при натурно-модельных испытаниях.
Результаты работы получены при поддержке гранта РФФИ № 14-08-01288 «Разработка теории натурно-модельных испытаний измерительных и исполнительных систем, построенных на основе ферромагнитных материалов с эффектом памяти формы».
Рецензенты:
Горбатенко Н.И., д.т.н., профессор, первый проректор, ФГБОУ ВПО «Южно-Российский государственный политехнический университет (НПИ) имени М.И. Платова», г. Новочеркасск;
Седов А.В., д.т.н., доцент, профессор кафедры «Автоматика и телемеханика», ФГБОУ ВПО «Южно-Российский государственный политехнический университет (НПИ) имени М.И. Платова», г. Новочеркасск.
Работа поступила в редакцию 17.10.2014.
Библиографическая ссылка
Гречихин В.В., Лозин О.И., Кудря А.В., Кудря Н.А., Шайхутдинов Д.В., Январев С.Г. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ДЕФОРМАЦИИ АКТИВНОГО ЭЛЕМЕНТА ИСПОЛНИТЕЛЬНОЙ СИСТЕМЫ НА ОСНОВЕ МАТЕРИАЛА С ПАМЯТЬЮ ФОРМЫ // Фундаментальные исследования. 2014. № 11-4. С. 744-748;URL: https://fundamental-research.ru/ru/article/view?id=35626 (дата обращения: 23.10.2025).



