Рассмотрение различных вопросов нелинейной динамики позволило по-новому посмотреть на соотношение непрерывного и дискретного при описании нелинейных процессов. Обнаруженное в 1980 г. М. Фейгенбаумом [1] сложное поведение сравнительно простого одномерного нелинейного отображения 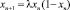 , n = 1, 2, ..., дающего при λ < 4 отображение отрезка [0, 1] в себя, было сразу замечено и использовано для разработки различных сценариев поведения нелинейных систем [2, 3], для уточнения таких понятий, как предельный цикл, аттрактор, область притяжения, бифуркации и т.п., универсальное поведение. Бифуркации удвоения периода, обнаруженные Фейгенбаумом стали одним из сценариев развития турбулентности в гидродинамике. Отметим, что исследование проведенное Фейгенбаумом – численное исследование при различных λ этого отображения.
, n = 1, 2, ..., дающего при λ < 4 отображение отрезка [0, 1] в себя, было сразу замечено и использовано для разработки различных сценариев поведения нелинейных систем [2, 3], для уточнения таких понятий, как предельный цикл, аттрактор, область притяжения, бифуркации и т.п., универсальное поведение. Бифуркации удвоения периода, обнаруженные Фейгенбаумом стали одним из сценариев развития турбулентности в гидродинамике. Отметим, что исследование проведенное Фейгенбаумом – численное исследование при различных λ этого отображения.
Здесь мы хотели бы привлечь внимание к одному, пока еще не востребованному, классу нелинейных уравнений, в которых регулярным образом можно получать решение в явном виде и тем самым аналитически выяснить зависимость решений от параметров модели, аналитически проследить перестройку решений при их изменении. Речь идет о мультипликативном рекуррентном автономном уравнении k-го порядка вида:
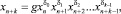 , n = 1, 2, ..., (1)
, n = 1, 2, ..., (1)
x1 = a1, x2 = a2, …, xk = ak, (1*)
в котором g > 0, ai > 0, i = 1, 2, ..., k, δj Î R, (j = 0, 1, ..., k – 1). Величины ai – начальные данные, а g и δj будем рассматривать как параметры модели (1).
Вид модели (1) с начальными условиями (1*) подсказывает, что решение (1) следует искать в виде
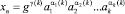 , n = 1, 2, ..., при выполнении (1*). (2)
, n = 1, 2, ..., при выполнении (1*). (2)
Искомая функция
xn = x(n, a1, a2, …, ak, δ0, δ1, …, δk–1)
будет определяться k + 1 функциями: k функциями αi(n) (i = 1, 2, …, k) и функцией γ(n) натурального аргумента.
Для нахождения функций αi(n) получаем – линейных однородных рекуррентных уравнений k-го порядка
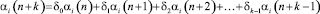 (3)
(3)
c начальными условиями
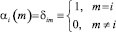 i, m = 1, 2, ..., k, (3*)
i, m = 1, 2, ..., k, (3*)
а для γ(n) – линейное неоднородное рекуррентное уравнение k-го порядка
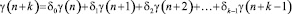 (4)
(4)
c нулевыми начальными условиями
γ(i) = 0, i = 1, 2, …, k. (4*)
Начальные условия (3*) и (4*) следуют из (2) и (1*).
Общее решение однородного линейного рекуррентного уравнения есть линейная комбинация k его частных линейно независимых решений, для нахождения которых нужно составить и решить характеристическое алгебраическое уравнение k-й степени с коэффициентами δ0, δ1, ..., δk–1.
Таким образом, аналитическое решение уравнения (1) с начальными условиями (1*) возможно в той мере, в какой возможно найти решение соответствующего характеристического алгебраического уравнения. В этой связи особое место среди мультипликативных уравнений (1) занимают уравнения второго и третьего порядков. Исследуем подробно уравнение второго порядка этого вида:
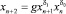 , n = 1, 2, ...; (5)
, n = 1, 2, ...; (5)
x1 = a > 0, x2 = b > 0, δ0, δ1 ∈ R.
Решение его ищем в виде (здесь a1 = a, a2 = b)
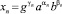 . (6)
. (6)
Для показателей αn и βn получаем линейные однородные рекуррентные уравнения второго порядка
αn+2 = δ1αn+1 + δ0αn, α1 = 1, α2 = 0; (7)
βn+2 = δ1βn+1 + δ0βn, β1 = 0, β2 = 1. (7*)
Их частные решения ищем в виде αn = βn = qn, n = 1, 2, ..., и для q получаем характеристическое уравнение
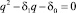 .
.
Его решение
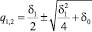 .
.
Случай 1. Корни действительные, различные,
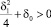
и
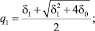
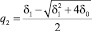 .
.
Общее решение тогда запишется в виде
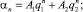
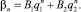 (8)
(8)
Для нахождения постоянных линейной комбинации имеем системы
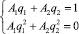
и
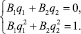
Решая, находим
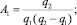
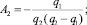
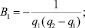
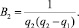
С учетом этого получаем
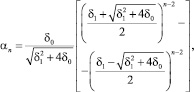 n = 2, 3, ...; (8*)
n = 2, 3, ...; (8*)
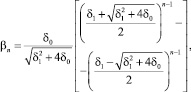 n = 1, 2, ... (8**)
n = 1, 2, ... (8**)
Случай 2. Корни комплексные,
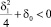 ,
, 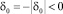 .
.
Тогда
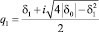 ;
;
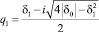 . (9)
. (9)
Запишем корни в виде
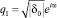 и
и 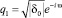 , (9*)
, (9*)
где 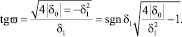 (10)
(10)
Если δ1 > 0, то
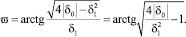 (10*)
(10*)
Если δ1 < 0, то
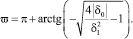 (10**)
(10**)
Общее решение αn и βn дается формулами (8), постоянные линейных комбинаций легко находятся, получаем
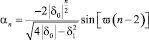 , n = 1, 2, ...; (11)
, n = 1, 2, ...; (11)
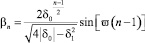 , n = 1, 2, ... (11*)
, n = 1, 2, ... (11*)
Значения ϖ и 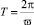 определяются комбинацией
определяются комбинацией  с учетом требований
с учетом требований 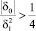 и δ0 < 0; «амплитуды» колебаний αn и βk меняются по закону
и δ0 < 0; «амплитуды» колебаний αn и βk меняются по закону 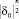 с изменением n и при δ0 = –1 от n не зависят. Зафиксировав значение
с изменением n и при δ0 = –1 от n не зависят. Зафиксировав значение  , мы тем самым фиксируем ϖ и T. Другими словами, если
, мы тем самым фиксируем ϖ и T. Другими словами, если 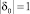 , то
, то
α n+T = αn, β n+T = βn, n = 1, 2, ...,
если 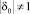 , то
, то
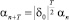 ,
, 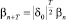 , n = 1, 2, ...,
, n = 1, 2, ...,
Случай 3.
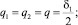
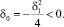
В этом случае
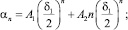
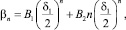 n = 1, 2, ...,
n = 1, 2, ...,
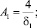
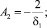
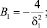
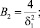
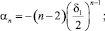
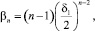 n = 1, 2, ... (12)
n = 1, 2, ... (12)
Для нахождения γn получаем неоднородное линейное рекуррентное соотношение второго порядка с нулевыми начальными условиями
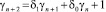 , n = 1, 2, ..., (13)
, n = 1, 2, ..., (13)
γ1 = 0, γ2 = 0, схема решения которого хорошо известна. При рассмотрении конкретного вида (5) удобнее все выкладки проводить с самого начала, а не пользоваться готовыми формулами.
Рассмотрим случай с δ0 = –1, δ1 = 1. Непосредственно легко убедиться, что уравнение
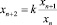 , n = 1, 2, ...,
, n = 1, 2, ...,
x1 = a, x2 = b (14)
задает периодическую последовательность с периодом Т = 6 и частотой 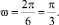 .
.
(xn): 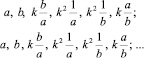 (15)
(15)
Члены этой последовательности имеют вид 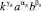 и с учетом (15) находим, что показатели γn, αn, βn – периодические, с периодом Т = 6
и с учетом (15) находим, что показатели γn, αn, βn – периодические, с периодом Т = 6
(γn): 0, 0, 1, 2, 2, 1; 0, 0, 1, 2, 2, 1;…
(αn): 1, 0, –1, –1, 0, 1; 1, 0, –1, –1, 0, 1; … (16)
(βn): 0, 1, 1, 0, –1, –1; 0, 1, 1, 0, –1, –1; …
Для любого n имеет место равенство
γn + αn + βn = 1, n = 1, 2, ...
Найдем аналитическую запись решения (15). Имеем
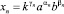 . (17)
. (17)
Получаем для определения показателей линейные рекуррентные уравнения
α n + 2 = α n + 1 – αn, α1 = 1, α2 = 0;
β n + 2 = β n + 1 – βn, β1 = 0, β2 = 1;
γ n + 2 = γ n + 1 – γ n + 1, γ1 = 0, γ2 = 1.
Характеристическое уравнение для этих уравнений имеет вид: 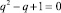 , а его корни:
, а его корни:
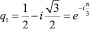 ;
;
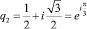
дают два частных решения 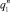 и
и 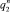 . Запишем общие решения этих уравнений и начальные условия:
. Запишем общие решения этих уравнений и начальные условия:
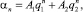 α1 = 1, α2 = 0;
α1 = 1, α2 = 0;
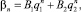 β1 = 0, β2 = 1;
β1 = 0, β2 = 1;
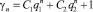 , γ1 = 0, γ2 = 0.
, γ1 = 0, γ2 = 0.
Определяя постоянные линейной комбинации, находим явные выражения для функций αn, βn, γn:
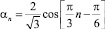 , n = 1, 2, ...;
, n = 1, 2, ...;
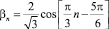 , n = 1, 2, ...;
, n = 1, 2, ...;
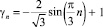 , n = 1, 2, ... (18)
, n = 1, 2, ... (18)
Решение уравнения (14), задаваемое формулами (17), (18), определяет функцию x = x(a, b, k, n). При фиксированных a, b, k она определяет периодическую числовую последовательность (5). Структура шести членов последовательности, составляющих период 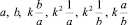 , такова, что изменение одного из этих трех параметров вызывает изменение только четырех чисел из этой шестерки.
, такова, что изменение одного из этих трех параметров вызывает изменение только четырех чисел из этой шестерки.
Частные эластичности этой функции по трем переменным будут равны соответствующим показателям:
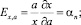
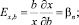
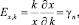 (19)
(19)
но полная эластичность этой функции [5]
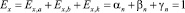 :
:
изменение всех параметров функции на 1 % вызовет изменение членов ряда (17) тоже на 1 %.
Рассмотренному случаю δ0 = –1, δ1 = 1 отвечает значение 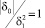 и согласно (10)
и согласно (10) 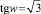 , так что
, так что 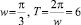 . Но значение
. Но значение 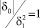 может достигаться и при других комбинациях δ0 и δ1, так для
может достигаться и при других комбинациях δ0 и δ1, так для 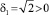 и δ0 = –2 имеем
и δ0 = –2 имеем 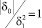 , так что
, так что 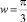 и Т = 6. В этом случае мы имеем дело с уравнением (k = g = 1)
и Т = 6. В этом случае мы имеем дело с уравнением (k = g = 1)
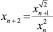 n = 1, 2, …, x1 = a, x2 = b
n = 1, 2, …, x1 = a, x2 = b
записано с помощью (11) и (11*):
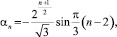 n = 1, 2, ...; (20)
n = 1, 2, ...; (20)
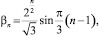 n = 1, 2, ... (20*)
n = 1, 2, ... (20*)
Убеждаемся, что
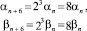 , n = 1, 2, ...
, n = 1, 2, ...
В качестве следующего примера рассмотрим случай, когда 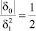 . Тогда при δ1 > 0 tgw = 1, соответственно
. Тогда при δ1 > 0 tgw = 1, соответственно 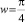 , а
, а 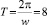 . Если δ0 = –1,
. Если δ0 = –1, 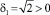 , то уравнение
, то уравнение
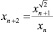 , x1 = a, x2 = b (21)
, x1 = a, x2 = b (21)
определяет периодическую числовую последовательность с периодом Т = 8, описываемую формулами
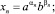
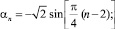
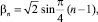 n = 1, 2, ... (22)
n = 1, 2, ... (22)
В этом случае |δ0| = 1, так что
α n + 8 = αn, β n + 8 = βn, n = 1, 2, ...
Если 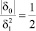 , но δ0 ≠ –1 и δ1 > 0, то
, но δ0 ≠ –1 и δ1 > 0, то
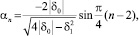 n = 1, 2, ...
n = 1, 2, ...
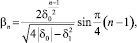 n = 1, 2, ... (23)
n = 1, 2, ... (23)
Возьмем δ0 = –2, δ1 = 2 > 0, 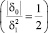 , тогда для последовательности
, тогда для последовательности
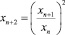 , n = 1, 2, ...,
, n = 1, 2, ...,
x1 = a, x2 = b. (24)
Получаем
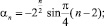
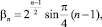 n = 1, 2, ...
n = 1, 2, ...
В этом случае
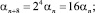
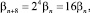 n = 1, 2, ...
n = 1, 2, ...
Соответственно, xn+8 = (xn)16 – восемь чисел очередного цикла получаются возведением в 16-ю степень чисел предыдущего цикла. Числа первой восьмерки этой последовательности
(xn): 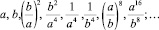
Если a = b, то (xn):
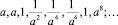
Если a ≠ 1, то при n → ∞, три числа из восьмерки цикла стремятся к нулю, три к бесконечности, два остаются равными единице.
Совсем по-другому ведут себя числа восьмерки цикла, если 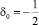 , δ1 = 1 > 0
, δ1 = 1 > 0 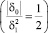 .
.
Имеем
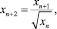 , n = 1, 2, ..., x1 = a, x2 = b. (26)
, n = 1, 2, ..., x1 = a, x2 = b. (26)
В этом случае
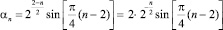 , n = 1, 2, ...
, n = 1, 2, ...
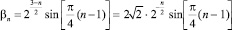 , n = 1, 2, ... (27)
, n = 1, 2, ... (27)
Находим, что
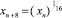 ,
, 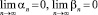 ,
,
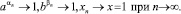
Если 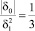 и δ1 > 0, то
и δ1 > 0, то 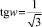 ;
; 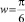 , а T = 12. Но при δ1 = –1, δ1 = –1 имеем
, а T = 12. Но при δ1 = –1, δ1 = –1 имеем 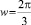 и Т = 3.
и Т = 3.
Если δ1 = δ0 = 1, то для уравнения
x n+2 = xnxn+1, n = 1, 2, ..., x1 = a, x2 = b.
Находим 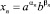 и
и
α n+2 = α n+1 + αn, α1 = 1, α2 = 0;
β n+2 = β n+1 + βn, β1 = 0, β2 = 1.
Оба уравнения определяют последовательность Фибоначчи с начальными данными 1,0 для αn и 0,1 для βn.
Проведенный здесь анализ свидетельствует о возможности аналитически изучать перестройку решений этого класса уравнений при изменении параметров модели.
Рецензенты:
Алтухов В.И., д.ф.-м.н., профессор, ведущий научный сотрудник отдела стратегического и инновационного развития СКФУ, филиал, г. Пятигорск;
Казуб В.Т., д.т.н., профессор, заведующий кафедрой физики и математики Пятигорского медико-фармацевтического института, филиал ГБОУ ВПО ВолгГМУ Минздрава РФ, г. Пятигорск.
Работа поступила в редакцию 05.08.2014.
Библиографическая ссылка
Абакумова С.И., Руденко В.Г., Стригун Н.С. ПЕРЕСТРОЙКА РЕШЕНИЙ РЕКУРРЕНТНОГО МУЛЬТИПЛИКАТИВНОГО УРАВНЕНИЯ ВТОРОГО ПОРЯДКА // Фундаментальные исследования. 2014. № 9-7. С. 1483-1488;URL: https://fundamental-research.ru/ru/article/view?id=35088 (дата обращения: 16.11.2025).



