В настоящее время большой практический и теоретический интерес представляет задача ускорения заряженных частиц ультракороткими лазерными импульсами большой интенсивностью в плазме [5–9]. Мощные лазерные импульсы используются как эффективное средство для получения высокоэнергичных частиц путем воздействия на фронтальную поверхность мишени из тонкой фольги [10, 11, 12].
Для оценки температуры быстрых электронов на фронтальной поверхности мишени в работе [11] было предложено использовать формулу кинетической энергии электрона, осциллирующего в поперечном поле падающей электромагнитной волны,
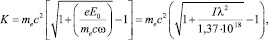 (1)
(1)
где me – масса электрона; c – скорость света; E0 – амплитуда электромагнитного поля падающей электромагнитной волны; ω – круговая частота; I – интенсивность падающей волны (в Вт/см2) λ – длина волны; (в мкм).
Решение уравнения движения заряженной частицы в поле плоской монохроматической электромагнитной волны в случаях линейной и круговой поляризации было получено в работе [2], и указано, что формула (1) соответствует нерелятивистскому случаю. В настоящей работе получено аналогичное решение для случая плоской монохроматической, эллиптически поляризованной электромагнитной волны, которое, как частные случаи, включает и указанное выше решение.
Цель настоящей работы – анализ движения частицы в поле эллиптически поляризованной электромагнитной волны и вывод формул для средней кинетической энергии частицы, усредненной по периоду её колебаний.
Постановка задачи
Уравнение движения частицы с массой m и зарядом q имеет вид
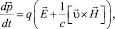 (2)
(2)
где 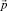 импульс частицы и ее скорость
импульс частицы и ее скорость  связаны равенством [3]
связаны равенством [3]
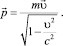 (3)
(3)
Изменение энергии частицы
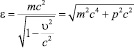 (4)
(4)
определяется уравнением
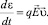 (5)
(5)
Энергия, импульс и скорость частицы связаны равенствами
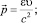
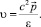 (6)
(6)
Будем считать, что волна распространяется вдоль оси z. В этом случае компоненты векторов электрического и магнитного поля волны определяются выражениями
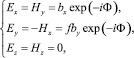 (7)
(7)
где 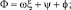
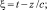 ω – частота несущей волны; ψ – параметр поляризации; φ – угол наклона осей эллипса к оси Ox системы координат; оси x и y совпадают с направлением полуосей эллипса поляризации волны bx и by, причем bx ≥ by ≥ 0; f = ±1 – параметр поляризации: верхний знак для Ey соответствует правой поляризации, а нижний – левой [4].
ω – частота несущей волны; ψ – параметр поляризации; φ – угол наклона осей эллипса к оси Ox системы координат; оси x и y совпадают с направлением полуосей эллипса поляризации волны bx и by, причем bx ≥ by ≥ 0; f = ±1 – параметр поляризации: верхний знак для Ey соответствует правой поляризации, а нижний – левой [4].
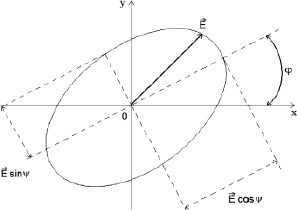
Рис. 1. Эллипс поляризации
Решение уравнения движения заряда
Решение уравнений (2) и (5) с 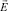 и
и 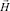 из (7) в действительной форме имеет вид
из (7) в действительной форме имеет вид
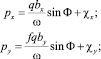
pz = γg; (8)
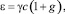
где χx, χy, γ – постоянные, причем выполняется условие
γ ≥ 0, т.е. ε ≥ mc2;
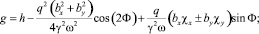 (9)
(9)
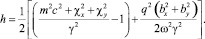 (10)
(10)
Из (8) и (6) получаем зависимость скорости частицы от фазы волны Φ:
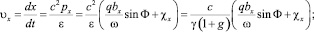
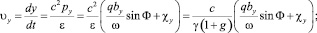 (11)
(11)
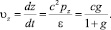
Постоянные χx и χy определяются начальной фазой волны
Φ0 = –kz0 + φ + ψ
и начальной скоростью υ0;
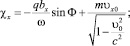
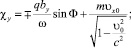 (12)
(12)
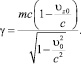
Из (11) получаем координаты частицы как функции Φ:
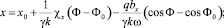
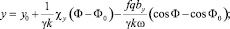
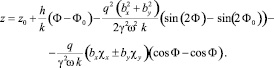 (13)
(13)
Движение частицы, усредненное по периоду колебаний
Здесь приведем результаты усреднения импульса 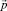 и энергии ε частицы по периоду ее колебаний в поле электромагнитной волны. Усреднение колебания частицы по её периоду проведем аналогично [2] с применением (8).
и энергии ε частицы по периоду ее колебаний в поле электромагнитной волны. Усреднение колебания частицы по её периоду проведем аналогично [2] с применением (8).
Для импульса частицы 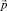 получаем следующие формулы:
получаем следующие формулы:
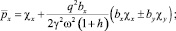
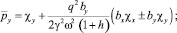 (14)
(14)
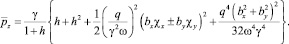
Для энергии ε частицы получаем
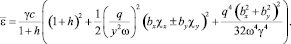 (15)
(15)
Из (15) видно, что  зависит от интенсивности волны, ее поляризации, начальной фазы, а также от начальной скорости частицы.
зависит от интенсивности волны, ее поляризации, начальной фазы, а также от начальной скорости частицы.
Случай эллиптической поляризации при отсутствии у частицы начальной скорости
Здесь рассмотрим случай, когда частица в начальный момент времени имеет скорость 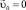 . Тогда уравнения (12) принимают вид
. Тогда уравнения (12) принимают вид
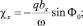
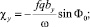 (16)
(16)
γ = mc.
Для волны с эллиптической поляризацией [1]
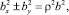 (17)
(17)
где ρ – параметр эллиптичности. При ρ = ±1 – соответствует линейной поляризации, а при 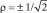 – круговой поляризации [1]. В остальных случаях величина ρ соответствует эллиптической поляризации
– круговой поляризации [1]. В остальных случаях величина ρ соответствует эллиптической поляризации 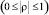 , при которой
, при которой
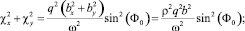 (18)
(18)
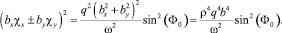 (19)
(19)
Из (10) получим значение h в начальный момент времени:
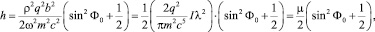 (20)
(20)
где 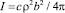 – интенсивность эллиптически поляризованной электромагнитной волны, а λ = 2πc/ω – длина волны.
– интенсивность эллиптически поляризованной электромагнитной волны, а λ = 2πc/ω – длина волны.
Подставляя (18), (19) и (20) в (15), получаем среднюю энергию первоначально покоящейся частицы в волне эллиптической поляризации
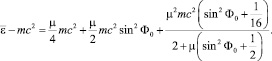 (21)
(21)
Как видно из (21), средняя энергия частицы зависит от интенсивности волны, параметра поляризации ψ, угла наклона φ осей эллипса к оси Ox системы координат, начальной фазы и скорости волны.
Усредняя по начальной фазе Φ0, средняя энергия заряженной частицы в поле плоской монохроматической эллиптически поляризованной волны имеет вид
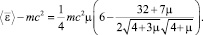 (22)
(22)
Для случая линейной поляризации при ρ = ±1 формула (22) принимает вид формулы (52) в [9].
На рис. 2. приведены зависимости средней кинетической энергии электрона от интенсивности плоской монохроматической электромагнитной волны линейной поляризации ρ = ±1, круговой поляризации 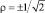 , круговой поляризации (формула (45)) из [2] и эллиптической поляризаций, представляющий наибольший практический интерес
, круговой поляризации (формула (45)) из [2] и эллиптической поляризаций, представляющий наибольший практический интерес 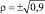 , а также энергии, рассчитанной по формуле (1).
, а также энергии, рассчитанной по формуле (1).
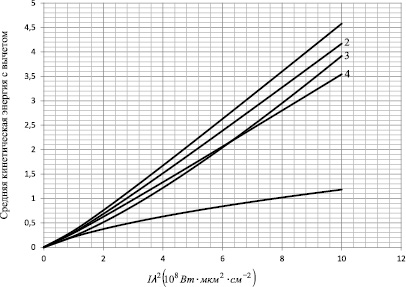
Рис. 2. Зависимости средней кинетической энергии электрона от интенсивности плоской монохроматической электромагнитной волны: 1 – линейной поляризации (ρ = ±1); 2 – эллиптической поляризации 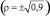 ; 3 – круговой поляризации
; 3 – круговой поляризации 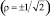 , 4 – круговой поляризации (формула (45) из [2]); K – расчет по формуле (1).
, 4 – круговой поляризации (формула (45) из [2]); K – расчет по формуле (1).
Как было указано в [2], формула (1) дает существенно заниженные значения средней кинетической энергии электрона в электромагнитном поле: при Iλ2 > 4,5·1018 Вт·мкм2·см–2 эти значения более чем в 2,5 раза меньше значений, рассчитанных по формуле для случая линейной поляризации, и более чем в 2,2 раза для круговой поляризации, рассчитанной по формуле (45) в [2]. Как видно из рис. 3, при усреднении значений фазовых характеристик для круговой поляризации значение средней кинетической энергии превосходит её значения на 0,4 МэВ значений, полученных по формуле (45) в [2]. Подставляя значения параметров ωξ0 = π/2, 3π/2; φ = π/2, 3π/2; ψ = π/2, 3π/2 и 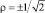 в (21), получаем формулу (45) из [2].
в (21), получаем формулу (45) из [2].
Для случая эллиптической поляризации 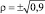 , что соответствует поляризации реального лазерного импульса большой интенсивности, значения средней кинетической энергии электрона в электромагнитном поле при Iλ2 > 4,5·1018 Вт·мкм2·см–2, на 0,25 МэВ больше этого значения для круговой поляризации и на 0,4 МэВ меньше для линейной поляризации.
, что соответствует поляризации реального лазерного импульса большой интенсивности, значения средней кинетической энергии электрона в электромагнитном поле при Iλ2 > 4,5·1018 Вт·мкм2·см–2, на 0,25 МэВ больше этого значения для круговой поляризации и на 0,4 МэВ меньше для линейной поляризации.
Заключение
В работе приведены точные решения уравнений движения заряженной частицы во внешнем поле эллиптически поляризованной электромагнитной волны. Исследованы различные случаи начальных условий движения заряженной частицы и поляризации волны. Вычислены значения импульса и энергии частицы, усредненные по периоду её колебаний. Полученные решения представлены в явной зависимости от начальных данных, амплитуды электромагнитной волны, интенсивности волны и её параметра поляризации, что позволяет применять полученные решения в практических расчетах.
Рецензенты:
Тумаев Е.Н., д.ф.-м.н., профессор, заведующий кафедрой теоретической физики и компьютерных технологий, Кубанский государственный университет, г. Краснодар;
Исаев В.А., д.ф.-м.н., доцент кафедры физики и информационных технологий, Кубанский государственный университет, г. Краснодар.
Работа поступила в редакцию 15.07.2014.
Библиографическая ссылка
Копытов Г.Ф., Мартынов А.А., Акинцов Н.С. ДВИЖЕНИЕ ЗАРЯЖЕННОЙ ЧАСТИЦЫ В ПОЛЕ ПЛОСКОЙ ЭЛЛИПТИЧЕСКИ ПОЛЯРИЗОВАННОЙ ЭЛЕКТРОМАГНИТНОЙ ВОЛНЫ // Фундаментальные исследования. 2014. № 9-5. С. 1013-1018;URL: https://fundamental-research.ru/ru/article/view?id=35007 (дата обращения: 15.11.2025).



