Оценка максимального допустимого тока высоковольтных силовых кабелей, проложенных в подземном кабельном канале, является важной задачей в сфере любых подземных разработок проектирования электрических сетей. На сегодняшний день электроэнергетика ожидает от подземных сетей высочайшую надежность и эффективную передачу электроэнергии.
В работе рассмотрена задача процессов тепломассообмена в кабельном канале. Исследуемый кабельный канал представляет собой бетонный монолит, находящийся на глубине одного метра от поверхности земли, в котором проложены трубы из полиэтилена с силовыми кабелями (рис. 1).
Пропускная способность кабельных линий напрямую зависит от температурного поля в кабельном канале. Для определения температурного поля необходимо решать задачу сложного тепломассообмена. Математическая модель движения и тепломассообмена в канале основывается на законах сохранения массы, количества движения и энергии [2, 6–7].
В зависимости от геометрии канала, передаваемой мощности и условий теплообмена в кабельном канале могут реализовываться различные режимы движения воздуха. Режим движения воздуха в кабельном канале существенно влияет на температуру и в конечном итоге на пропускную способность кабелей. Выбор того или иного режима движения воздуха можно оценивать по критерию Рейнольдса [1]. Для рассматриваемой геометрии канала и условий теплообмена расчетный критерий Рейнольдса не превышает 600 единиц. В этом случае естественным было бы предположить, что реализуется ламинарное движение воздуха в канале. Были сделаны следующие допущения: задача стационарная, движение воздушного потока ламинарное; теплофизические характеристики материалов постоянны; сложная конструкция конструктивных элементов кабеля заменена однородным слоем из полиэтилена c эквивалентными свойствами.
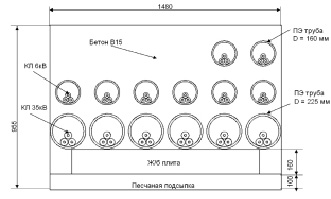
Рис. 1. Конструктивные элементы кабельного канала и используемые материалы
Система дифференциальных уравнений, описывающая процессы тепломассообмена в условиях естественной конвекции, имеют вид [3]:
Уравнение неразрывности:
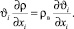 (1)
(1)
Уравнение движения:
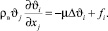 (2)
(2)
Уравнение энергии для воздуха:
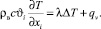 (3)
(3)
Уравнение теплопроводности для кабельных линий:
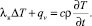 (4)
(4)
Уравнение теплопроводности земли:
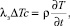 (5)
(5)
Плотность воздуха зависит от температуры по закону Буссинеска [8]:
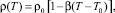 (6)
(6)
где ρ – плотность материала; ρв – плотность воздуха (в зависимости от температуры); xi – декартовые координаты; ϑi – компоненты вектора скорости воздуха в канале; fi – сила конвективного переноса; c – теплоемкость среды; T – температура; λ – теплопроводность воздуха; qv – мощность внутренних источников тепла; λк – теплопроводность конструктивных элементов кабельного канала; λз – теплопроводность земли; μ – динамическая вязкость воздуха.
Конвективный теплообмен между кабелями и стенками полиэтиленовой трубы дополняется теплообменом излучением.
Система уравнений (1)–(6) замыкалась следующими граничными условиями: на твердых непроницаемых границах канала и на поверхности кабелей для компонент скоростей воздуха задается условие прилипания и непроникновения; на поверхности земли задано граничное условие третьего рода; на трех других границах в массиве земли заданы адиабатические условия теплообмена; на границах контакта разнородных сред задавались граничные условия четвертого рода.
Поставленная задача решалась с помощью метода конечных элементов [4, 5].
Для проверки адекватности предложенной модели были произведены численные расчеты методом конечных элементов и произведено сравнение с натурными данными.
Для исследуемого кабельного канала были сделаны натурные измерения, которые проводились с помощью бесконтактного пирометра ТКА.
В табл. 1 приведены условия, при которых происходили замеры температуры в кабельном канале.
В результате решения поставленной задачи было получено температурное поле в кабельном канале. На рис. 2 показан увеличенный масштаб кабельной линии, находящейся под токовой нагрузкой. Рабочий ток одного кабеля составляет 107 А.
Таблица 1
|
Время, число, месяц, год |
11 часов, 05.07.2012, ясная погода |
|
Температура грунта, °С |
15 |
|
Температура воздуха, °С |
26 |
|
Токовая нагрузка одной кабельной линии, А |
107 |
|
Токовая нагрузка второй кабельной линии, А |
13 |
|
Температура первой кабельной линии, °С |
25,7 |
|
Температура воздуха в первой трубе, °С |
23,0 |
|
Температура второй кабельной линии, °С |
22,0 |
|
Температура воздуха во второй трубе, °С |
21,3 |
Максимальная температура на поверхности первой кабельной линии составляет 26,4 °С, температура воздуха в трубе 23,4 °С. Для второй кабельной линии 21,6 и 21,2 °С соответственно. Расхождение с табл. 1 составило не более 5 %. Этой погрешностью можно пренебречь в силу масштабности поставленной задачи.
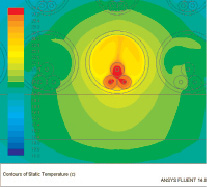
Рис. 2. Температурное поле кабельной линии
Управление нагрузочной способности кабельных линий в зависимости от режимов нагружения
Представлены картины распределения температурных полей при различных режимах нагрузки кабельных линий после решения поставленной задачи.
На рис. 3 представлено температурное поле в кабельном канале и в массиве земли при максимально допустимых нагрузках кабелей для данных условий прокладки и работы кабельных линий.
По полученному температурному полю можно определить кабельные линии, находящиеся в более жестких температурных условиях. Видно, что кабели, расположенные ближе к центральной области канала, более нагреты, чем кабели, расположенные на периферии. Это необходимо учитывать при распределении нагрузки по каналу. Максимальная температура не превышает допустимой температуры для данных условий прокладки.
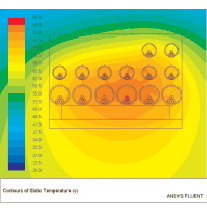
Рис. 3. Температурное поле кабельного канала при работе всех кабельных линий
Таблица 2
Эксплуатационные характеристики кабелей при различных режимах нагружения
|
Эксплуатационные характеристики |
Количество работающих кабельных линий |
||||
|
1 |
6 |
8 |
14 |
||
|
Tmax, °С |
90 |
90 |
90 |
90 |
|
|
Рабочий ток, А |
274 |
134,4 |
127 |
115,7 |
|
|
Передаваемая мощность по одной линии, МВА |
На 6 кВ |
– |
– |
1,32 |
9,62 |
|
На 35 кВ |
16,6 |
8,14 |
– |
42,1 |
|
|
Суммарная передаваемая мощность в канале, МВА |
16,6 |
48,9 |
10,6 |
51,72 |
|
В табл. 2 сведены результаты расчетов по определению эксплуатационных характеристик кабельных линий при различных режимах нагружения. Данные рекомендации по значениям токовых нагрузок полностью соответствуют критерию непревышения максимальной допустимой температуры, равной для данного типа изоляции 90 °С, которая реализуется в кабельном канале.
Исходя из результатов, представленных в табл. 2 видно, что в случае если необходимо передавать максимальную мощность по кабельным линиям на 35 кВ, отключаем кабельные линии на 6 кВ и увеличиваем рабочий ток на 16 %. Если в случае когда кабельный канал нагружен до максимальной нагрузки и рабочий ток всех кабельных линий равен 115,7 А, то при работе только кабельных линий на 35 кВ рабочий ток уже составит 134,4 А, а суммарная передаваемая мощность будет равна 48,9 МВА.
Управление нагрузочной способности кабельных линий в зависимости от климатических условий
В наше время актуальной является проблема загруженности кабельных линий. Особую роль играют влияния климатических факторов, таких как, например, температура поверхности земли. В зимнее время возникает потребность увеличения нагрузки на кабель, которую можно обосновать, проведя исследование влияния климатических условий на температурное поле в канале и соответствующего выбора уровня передаваемой мощности.
На рис. 4 представлен график зависимости максимальной температуры в кабельном канале от температуры грунта при работе всех кабельных линий.
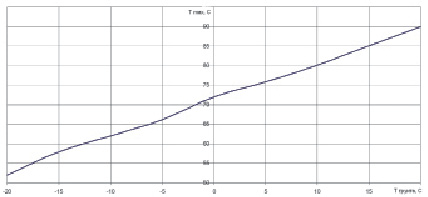
Рис. 4. Зависимость максимальной температуры в кабельном канале от температуры окружающего грунта
За основу взяты расчеты по определению температуры в кабельном канале при допустимой нагрузке всех кабелей. Температура грунта составляет 20 °С, а рабочий ток для кабельных линий равен 115,7 А. Из рис. 4 видно, что при уменьшении температуры грунта температура в кабельном канале уменьшается. Данное понижение температуры дает возможность увеличить пропускную способность кабельных линий в зимнее время года, когда потребности потребителей растут. Для оптимизации передаваемой мощности по кабельным линиям в зависимости от климатических условий была осуществлена итерационная процедура по подбору рабочего тока для диапазона температур поверхности таким образом, чтобы температура изоляции не превышала допустимой температуры сшитого полиэтилена. В табл. 3 приведены эксплуатационные характеристики кабельного канала для различных температурных условий окружающего грунта. Также приведены рекомендуемые максимально допустимые токовые нагрузки в зависимости от температурных условий окружающего грунта.
Данные рекомендации актуальны при работе всех кабельных линий.
Таблица 3
Эксплуатационные характеристики кабельного канала
|
Эксплуатационные характеристики |
Температура окружающего грунта, °С |
||||||||
|
‒20 |
‒15 |
‒10 |
‒5 |
0 |
+5 |
+10 |
+15 |
+20 |
|
|
Максимальная температура в канале, °С |
52 |
58 |
62 |
66 |
72,2 |
75,8 |
80 |
85 |
90 |
|
Рабочий ток кабельных линий, А |
115,7 |
115,7 |
115,7 |
115,7 |
115,7 |
115,7 |
115,7 |
115,7 |
115,7 |
|
Допустимый рабочий ток (Температура в канале 90 °С) |
140,7 |
136,6 |
133,3 |
130,4 |
127,7 |
125,3 |
122,8 |
119,5 |
115,7 |
|
Увеличение нагрузочной способности, % |
21,7 |
18,1 |
15,3 |
12,8 |
10,3 |
8,3 |
6,1 |
3,3 |
0 |
|
Суммарная передаваемая мощность, МВА |
62,9 |
61,1 |
59,6 |
58,2 |
57,07 |
55,94 |
54,89 |
53,39 |
51,72 |
Исходя из результатов, представленных в табл. 3, видно, что в зимнее время года, когда грунт охлаждается до отрицательной температуры, появляется возможность увеличивать токовую нагрузку до 20 % и тем самым повысить значение суммарной передаваемой мощности на 21 %. Все полученные результаты позволяют оперативно оценить максимальную пропускную способность кабельных линий по заданным условиям, спроектировать новую линию «с нуля» или модернизировать старую.
Работа выполнена при финансовой поддержке РФФИ (грант № 13-08-96034).
Рецензенты:
Щербинин А.Г., д.т.н., профессор кафедры «Конструирование и технологии в электротехнике», Пермский национальный исследовательский политехнический университет, г. Пермь;
Бочкарев С.В., д.т.н., профессор кафедры «Микропроцессорные средства автоматизации», Пермский национальный исследовательский политехнический университет, г. Пермь.
Работа поступила в редакцию 15.07.2014.
Библиографическая ссылка
Навалихина Е.Ю., Труфанова Н.М. КОМПЬЮТЕРНАЯ МОДЕЛЬ ПРОЦЕССОВ ТЕПЛОМАССОПЕРЕНОСА В КАБЕЛЬНОМ КАНАЛЕ ПРИ РАЗЛИЧНЫХ РЕЖИМАХ РАБОТЫ КАБЕЛЬНЫХ ЛИНИЙ // Фундаментальные исследования. 2014. № 9-5. С. 988-992;URL: https://fundamental-research.ru/ru/article/view?id=35002 (дата обращения: 15.01.2026).



