Динамика вибромашины с параметрическим возбуждением при прямолинейных колебаниях рабочего органа исследовалась в работах [1, 2, 4, 5, 7]. При этом необходимая форма траектории обеспечивалась однонаправленной упругой системой.
Многие вибрационные технологии для их осуществления требуют возбуждения и поддержания стабильных поступательных круговых колебаний рабочего органа машины. Например, для сверхтонкого измельчения материалов используются шаровые вибрационные мельницы с зарезонансной настройкой, корпус которых совершает поступательные круговые колебания. Эти мельницы характеризуются низкой производительностью и высоким уровнем энергопотребления. Резонансные режимы вибромельниц, являющиеся наиболее эффективными, практически нереализуемы из-за их низкой стабильности при обычном резонансе вынужденных колебаний. Поэтому поиск альтернативных способов возбуждения и стабилизации резонансных машин является весьма актуальным.
Чтобы осуществить поступательные круговые колебания рабочего органа машины, необходимо учесть его перемещение в двух взаимно перпендикулярных направлениях по осям x, y и образовать упругое изотропное поле путем введения упругих элементов с одинаковой жесткостью cx = cy = c.
Целью данной работы является исследование динамики вибрационной машины с изотропной упругой системой, принцип действия которой основан на самовозбуждении многократного комбинационного параметрического резонанса.
Материалы и методы исследования
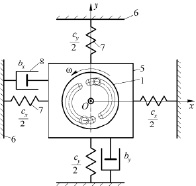
Для реализации резонансных колебаний используется параметрический вибровозбудитель. В отличие от инерционного (дебалансного) вибровозбудителя с вращательным движением инерционного элемента (ИЭ), параметрический вибровозбудитель – это резонансный инерционный вибровозбудитель с колебательным движением ИЭ. Основным узлом параметрического вибровозбудителя является роторно-маятниковая система. На рис. 1 приведена динамическая модель вибрационного устройства. Механизм ИЭ вибровозбудителя выполнен по патенту № 2410167 [11].
Ротор 1 этой системы состоит из набора отдельных одинаковых уравновешенных дисков 2 (рис. 1б). В каждом диске образована пара незамкнутых беговых дорожек 3 кругового профиля, которые расположены симметрично относительно двух взаимно перпендикулярных его диаметров, а их центры смещены от оси вращения ротора в диаметрально противоположных направлениях на одинаковые расстояния AB = l. На беговых дорожках размещены одинаковые уравновешенные тела качения (маятники) 4 массой m каждый с возможностью обкатки. Диски соединяются между собой в единую конструкцию так, что беговые дорожки одной пары повернуты вокруг оси ротора на угол γ0 = π/s относительно другой, где s – число дисков (s = 2).
 а
а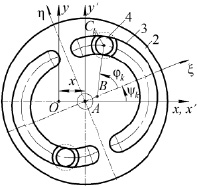 б
б
Рис. 1. Динамическая модель вибрационного устройства
Ротор ИЭ содержит N = 2s тел качения (маятников), расположенных попарно в параллельных плоскостях. Ротор ИЭ массой m0 в собранном виде жестко закрепляется на приводном валу, который посредством подшипников устанавливается на рабочем органе 5 массой M0. Рабочий орган связан с основанием 6 упругими элементами 7. Демпфер 8 отображает трение от технологической нагрузки.
Система координат Ax′y′z′ с началом в центре масс ротора ИЭ движется поступательно относительно неподвижной системы Oxyz. При этом плоскость Ax′y′ расположена в плоскости вращения ротора. В положении статического равновесия оси этих координатных систем совпадают. Приводной вал получает вращение от электродвигателя, вынесенного из колебательной системы машины. При этом на движение тел качения накладываются нестационарные (реономные) связи за счет равномерного вращения ротора ИЭ с угловой скоростью ω, что предполагает наличие идеального источника энергии. Это предположение на самом деле не столь существенно, поскольку ротор ИЭ с развитым моментом инерции выполняет роль маховика и аккумулятора кинетической энергии. При равномерном вращении ротора ИЭ тела качения образуют в поле центробежных сил инерции подсистему N осцилляторов качения (маятников) с осями обкатки в центрах кривизны беговых дорожек.
Положение беговых дорожек определяется углами 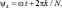 а положение маятников определяется углами φk, k = 1, 2, …, N. Предполагается, что выполнены условия, при которых осцилляторы качения колеблются без скольжения и отрыва, полученные в работе [9].
а положение маятников определяется углами φk, k = 1, 2, …, N. Предполагается, что выполнены условия, при которых осцилляторы качения колеблются без скольжения и отрыва, полученные в работе [9].
Примем параметры x, y, φk, где x, y – перемещение рабочего органа, за обобщенные координаты системы.
Характеристики восстанавливающих сил и сил сопротивления задаются в виде:
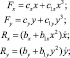
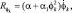 k = 1, 2, ..., N,
k = 1, 2, ..., N,
где cx = cy = c – суммарная жесткость упругих элементов в направлении осей x, y соответственно; c1x = c1y = c1 – коэффициент нелинейности упругих восстанавливающих сил в соответствующих направлениях; bx = by = b, α – коэффициенты линейного демпфирования, b1x = b1y = b1, α1 – коэффициенты нелинейного демпфирования.
Будем исходить из дифференциальных уравнений движения, полученных в работе [3]. Если ввести безразмерное время τ = λ2t, безразмерные координаты 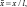
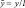 и удержать в указанных уравнениях величины до третьего порядка относительно координат и их производных, то математическую модель вибрационной машины с изотропной упругой системой можно записать в следующем виде:
и удержать в указанных уравнениях величины до третьего порядка относительно координат и их производных, то математическую модель вибрационной машины с изотропной упругой системой можно записать в следующем виде:
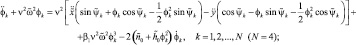
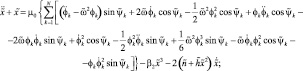
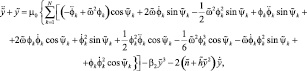 (1)
(1)
где β1 = 1/6; 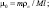
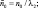
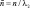 – безразмерные коэффициенты линейного демпфирования;
– безразмерные коэффициенты линейного демпфирования; 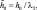
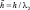 – безразмерные коэффициенты нелинейного демпфирования; β2 = γl2 – коэффициент нелинейности упругих восстанавливающих сил;
– безразмерные коэффициенты нелинейного демпфирования; β2 = γl2 – коэффициент нелинейности упругих восстанавливающих сил; 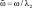 – безразмерная частота параметрического возбуждения;
– безразмерная частота параметрического возбуждения; 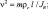
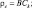
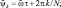 γ = c1/c. Здесь M = M0 + m0 + Nm – общая масса системы; JB – момент инерции тела качения относительно оси обкатки, n0 = α/2JB, n = b/2M, h0 = α1/(2JB), h = b1/(2M). Точка обозначает дифференцирование по τ.
γ = c1/c. Здесь M = M0 + m0 + Nm – общая масса системы; JB – момент инерции тела качения относительно оси обкатки, n0 = α/2JB, n = b/2M, h0 = α1/(2JB), h = b1/(2M). Точка обозначает дифференцирование по τ.
Уравнения (1) описывают поведение N + 2 равноправных нелинейных осцилляторов и системы связи между ними. Первые N уравнений системы (1) описывают колебания тел качения ИЭ как физических маятников с осями подвеса в центрах кривизны беговых дорожек во вращающейся системе координат Aξηζ.
Исследуем комбинационный параметрический резонанс, когда колебания в системе (1) возбуждаются на частотах ω1 и ω2, связанных с частотой параметрического возбуждения  соотношением
соотношением
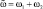 , (2)
, (2)
причем частоты генерации близки к собственным частотам, т.е. 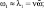
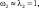 и некратны между собой. Параметр ν определяет собственную частоту колебаний осцилляторов во вращающейся системе координат. При вертикальном расположении плоскости вращения ротора ИЭ силы тяжести маятников порождают нестационарное силовое поле. В [8] показано, что при настройке ν = 0,25 влиянием сил тяжести маятников можно пренебречь.
и некратны между собой. Параметр ν определяет собственную частоту колебаний осцилляторов во вращающейся системе координат. При вертикальном расположении плоскости вращения ротора ИЭ силы тяжести маятников порождают нестационарное силовое поле. В [8] показано, что при настройке ν = 0,25 влиянием сил тяжести маятников можно пренебречь.
Для отыскания решения системы (1) воспользуемся методом усреднения. Сделаем предположение о малости сил трения и нелинейных сил. Введем в рассмотрение параметр 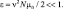 Этот параметр пропорционален отношению общей массы осцилляторов качения к массе всей системы. Для реальных динамических систем величина ν лежит в пределах: ν = 0,2–0,5. Параметр ν связан с параметром ε соотношением
Этот параметр пропорционален отношению общей массы осцилляторов качения к массе всей системы. Для реальных динамических систем величина ν лежит в пределах: ν = 0,2–0,5. Параметр ν связан с параметром ε соотношением 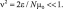 . В качестве малого параметра можно взять параметр ε. Но при ε = 0 уравнения системы (1) для координат φk, k = 1, 2, ..., N превращаются в равенства
. В качестве малого параметра можно взять параметр ε. Но при ε = 0 уравнения системы (1) для координат φk, k = 1, 2, ..., N превращаются в равенства 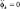 . Таким образом утрачивается стандартная (в смысле Н.Н. Боголюбова) форма уравнений системы (1). Поэтому стандартный алгоритм метода усреднения не может быть использован. Введение малого параметра дает возможность выделить группу ведущих членов, определяющих общий характер решения уравнений (1). Благодаря специфике введения малого параметра μ в конечные соотношения метода усреднения входят только исходные параметры системы и необходимость в конкретном определении параметра μ не возникает. Поэтому для привидения системы уравнений (1) к стандартной форме воспользуемся приемом, предложенным в [9] и запишем уравнения (1) в виде
. Таким образом утрачивается стандартная (в смысле Н.Н. Боголюбова) форма уравнений системы (1). Поэтому стандартный алгоритм метода усреднения не может быть использован. Введение малого параметра дает возможность выделить группу ведущих членов, определяющих общий характер решения уравнений (1). Благодаря специфике введения малого параметра μ в конечные соотношения метода усреднения входят только исходные параметры системы и необходимость в конкретном определении параметра μ не возникает. Поэтому для привидения системы уравнений (1) к стандартной форме воспользуемся приемом, предложенным в [9] и запишем уравнения (1) в виде
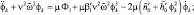
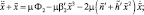 (3)
(3)
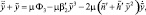
где 

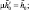


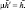 . Здесь выражения μФ1, μФ2, μФ3 равны соответственно правым частям уравнений (1), заключенным в квадратные скобки с множителем ν2 и в фигурные скобки с множителем μ0.
. Здесь выражения μФ1, μФ2, μФ3 равны соответственно правым частям уравнений (1), заключенным в квадратные скобки с множителем ν2 и в фигурные скобки с множителем μ0.
Принимая во внимание, что стационарные колебания рабочего органа в горизонтальной и вертикальной плоскостях сдвинуты по фазе на четверть периода (Δθ = –π/2), решение уравнений (1) будем искать в виде
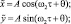
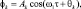 k = 1, 2, …, N. (4)
k = 1, 2, …, N. (4)
Принимая A, Ak, θ, θk за новые медленные переменные и применяя метод усреднения [10], получим для них следующие усредненные уравнения первого приближения:
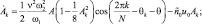
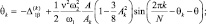
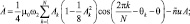 (5)
(5)
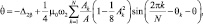
k = 1, 2, …, N,
где 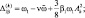
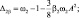
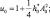
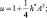
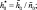
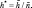 Величины
Величины 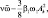
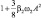 можно рассматривать как парциальные частоты, смещенные за счет нелинейности системы.
можно рассматривать как парциальные частоты, смещенные за счет нелинейности системы.
Искомый стационарный режим работы вибрационной машины получается как особые точки системы (5). Они будут решениями уравнений (5) при равных нулю правых частях, т.е. 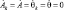 . Это приводит к системе алгебраических нелинейных уравнений относительно амплитуд A, Ak и фаз θ, θk. Поскольку осцилляторы качения идентичны, то Ak = A0, k = 1, 2, …, N. Указанные уравнения разрешались при выполнении условий
. Это приводит к системе алгебраических нелинейных уравнений относительно амплитуд A, Ak и фаз θ, θk. Поскольку осцилляторы качения идентичны, то Ak = A0, k = 1, 2, …, N. Указанные уравнения разрешались при выполнении условий
θk = 2πk/N, k = 1, 2, …, N. (6)
В результате приходим к следующим уравнениям:
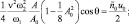
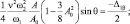
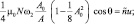
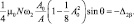 (7)
(7)
Из первого и третьего уравнений (7) найдем отношение амплитуд
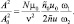 (8)
(8)
Из уравнений (7) можно определить tgθ и соотношение между расстройками
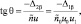 (9)
(9)
где 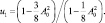
Теперь сложим попарно первое и третье уравнения системы (7), а также второе и четвертое и избавимся от тригонометрических функций. Примем в качестве расстройки величину 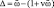 , т.е. расстройку частоты параметрического возбуждения относительно суммы собственных частот и, используя равенство (2), которое теперь принимает вид
, т.е. расстройку частоты параметрического возбуждения относительно суммы собственных частот и, используя равенство (2), которое теперь принимает вид 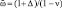 , после некоторых преобразований получим уравнение
, после некоторых преобразований получим уравнение
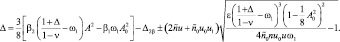 (10)
(10)
Воспользовавшись соотношениями (8), (2), приходим к уравнению:
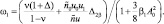 (11)
(11)
Уравнения (10) и (11) позволяют численными методами определить зависимости A(Δ), ω1(Δ), ω2(Δ). Величины u0, u содержат 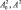 , поэтому соотношение (8) приводит к биквадратному уравнению относительно A. Это уравнение имеет решение
, поэтому соотношение (8) приводит к биквадратному уравнению относительно A. Это уравнение имеет решение 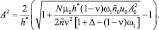 Из уравнения (10) следует условие существования стационарных колебаний, которое с учетом соотношения
Из уравнения (10) следует условие существования стационарных колебаний, которое с учетом соотношения 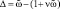 , принимает вид
, принимает вид
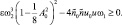 (12)
(12)
Неравенство (12) удовлетворяется тогда, когда при линейном демпфировании выполняется пороговое условие
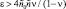 (13)
(13)
и когда амплитуды A0, A не превышают своих максимальных значений. Сравнение условия (13) с аналогичным условием для однонаправленной упругой системы показывает, что для вибромашины с изотропной упругой системой пороговое значение снижается в два раза. Это позволяет в два раза снизить массу инерционного элемента машины.
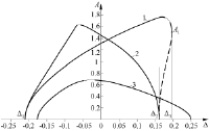
Результаты численного моделирования уравнений (10) и (11) методом итераций представлены на рис. 2 в виде зависимостей амплитуды A, частот генерации ω1, ω2 от расстройки Δ.
 а
а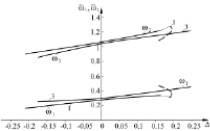 б
б
Рис. 2. Резонансные кривые и частоты генерации
На рис. 2а кривая 1 соответствует комбинационному резонансу, когда ε = 0,01, n = 0,25, 
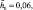
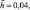 β1 = 1/6, β2 = 0,17 Резонансная кривая 2 соответствует случаю, когда β2 = 0,
β1 = 1/6, β2 = 0,17 Резонансная кривая 2 соответствует случаю, когда β2 = 0, 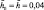 при неизменных значениях остальных параметров. Резонансная кривая 3 построена для величин
при неизменных значениях остальных параметров. Резонансная кривая 3 построена для величин 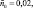
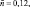
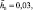
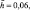 β2 = 0 и тех же значений других параметров, что и кривая 1. Резонансные кривые A0 = A0(Δ) имеют аналогичный вид, что следует из соотношения (8). В точках резонансных кривых, отмеченных тонкой линией, процесс итераций расходится. Граничные точки Δ1 = –0,2083, Δ2 = 0,1594, являющиеся основанием резонансной кривой 1, определяются из уравнений (10) и (11) при A = A0 = 0. Эти точки не зависят от нелинейностей и совпадают с границами области неустойчивости (резонансной зоны) определяемыми методами линейной теории на основе численной реализации теории Флоке ‒ Ляпунова [3, 5]. На рис. 2, б приведены зависимости ω1, ω2 от Δ в полосе параметрической генерации, соответствующие амплитудным кривым 1 и 3.
β2 = 0 и тех же значений других параметров, что и кривая 1. Резонансные кривые A0 = A0(Δ) имеют аналогичный вид, что следует из соотношения (8). В точках резонансных кривых, отмеченных тонкой линией, процесс итераций расходится. Граничные точки Δ1 = –0,2083, Δ2 = 0,1594, являющиеся основанием резонансной кривой 1, определяются из уравнений (10) и (11) при A = A0 = 0. Эти точки не зависят от нелинейностей и совпадают с границами области неустойчивости (резонансной зоны) определяемыми методами линейной теории на основе численной реализации теории Флоке ‒ Ляпунова [3, 5]. На рис. 2, б приведены зависимости ω1, ω2 от Δ в полосе параметрической генерации, соответствующие амплитудным кривым 1 и 3.
Для исследования устойчивости особых точек, соответствующих стационарному режиму колебаний, составлялись уравнения в вариациях относительно этих особых точек, которые здесь не приводятся из-за их громоздкости. Система десяти дифференциальных уравнений первого порядка в вариациях преобразуется в эквивалентную систему относительно суммы и разности вариаций амплитуд и фаз осцилляторов ИЭ. Устойчивость преобразованных уравнений определялась с помощью критерия Гурвица.
Результаты исследования и их обсуждение
Анализ устойчивости стационарных решений рассмотрим на примере резонансной кривой 1. Внутри интервала ∆1 < ∆ < ∆2 тривиальное решение (положения равновесия) неустойчиво, а нетривиальное решение – устойчиво. Стационарные решения в интервале ∆2 < ∆ < ∆3 являются многозначными. Из трех возможных значений амплитуды установившихся колебаний устойчивым колебаниям соответствует тривиальное решение (колебания с нулевой амплитудой) и нетривиальное решение с наибольшей амплитудой, а неустойчивым – с наименьшей амплитудой. Сплошными линиями показаны асимптотически устойчивые решения, а штриховыми – неустойчивые.
Точка ∆ = ∆1 является точкой бифуркации, при переходе которой положение равновесия теряет устойчивость и возникает неравновесное состояние – периодические колебания. Этот вид потери устойчивости называется мягкой потерей устойчивости, т.к. устанавливающийся колебательный режим при малой закритичности ε* = ∆-∆1 (отличие параметра ∆ от критического значения ∆1) мало отличается от равновесия. При переходе ε* через нуль устойчивый фокус становится неустойчивым и рождается устойчивый предельный цикл малой амплитуды, что соответствует динамической бифуркации Андронова ‒ Хопфа.
Как видно из рис. 2, а обнаруживается эффект расширения резонансной зоны при шестикратном увеличении линейного демпфирования рабочего органа относительно уровня демпфирования осцилляторов ИЭ.
Рассмотрим принцип действия вибрационной машины с изотропной упругой системой. Для этого воспользуемся формулами для определения центра масс маятников по отношению к неподвижной системе координат Oxyz. Пусть 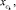
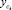 – координаты центра масс k-го осциллятора качения. Тогда координаты xc, yc центра масс системы осцилляторов могут быть вычислены по формулам:
– координаты центра масс k-го осциллятора качения. Тогда координаты xc, yc центра масс системы осцилляторов могут быть вычислены по формулам:
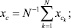
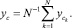 (14)
(14)
Координаты 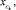
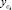 определяются формулами
определяются формулами
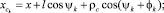
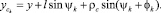 (15)
(15)
Заменяя тригонометрические функции углов φk двумя членами разложения их в ряд и выполняя преобразования, описанные в [6], получим следующие формулы для центра масс системы бегунков при N = 4:
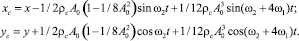 (16)
(16)
Вычислим силу 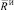 , действующую на рабочий орган машины от качающихся осцилляторов ИЭ. На основании теоремы о движении центра масс механической системы проекции главного вектора
, действующую на рабочий орган машины от качающихся осцилляторов ИЭ. На основании теоремы о движении центра масс механической системы проекции главного вектора 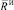 на оси координат могут быть определены по формулам
на оси координат могут быть определены по формулам 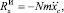
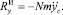 Если составить дифференциальные уравнения колебаний рабочего органа под действием указанных сил, то увидим, что правые части этих уравнений представляют собой сумму гармонических вынуждающих сил с частотами ω2 и ω2 + 4ω1. Вторая составляющая вынуждающих сил имеет далеко зарезонансную настройку и ее влиянием можно пренебречь. Тогда закон движения центра масс системы осцилляторов ИЭ в первом приближении принимает вид
Если составить дифференциальные уравнения колебаний рабочего органа под действием указанных сил, то увидим, что правые части этих уравнений представляют собой сумму гармонических вынуждающих сил с частотами ω2 и ω2 + 4ω1. Вторая составляющая вынуждающих сил имеет далеко зарезонансную настройку и ее влиянием можно пренебречь. Тогда закон движения центра масс системы осцилляторов ИЭ в первом приближении принимает вид
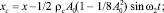
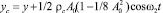 . (17)
. (17)
Координаты центра масс маятников по отношению к системе координат Ax’y’z’ с началом в центре ротора ИЭ выражаются формулами 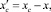
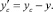 В этой системе координат центр масс системы осцилляторов ИЭ описывает окружность в плоскости вращения ротора ИЭ согласно закону:
В этой системе координат центр масс системы осцилляторов ИЭ описывает окружность в плоскости вращения ротора ИЭ согласно закону:
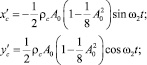
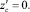 (18)
(18)
Угловая скорость его вращения по этой окружности равна частоте ω2 ≈ λ2 колебаний рабочего органа. Таким образом, автоматически образуется неуравновешенность ИЭ (невидимый дебаланс). Поскольку ω2 ≈ λ2, то неуравновешенная центробежная сила инерции будет возбуждать резонансные колебания рабочего органа. При этом существенна взаимосвязь колебаний: колебания рабочего органа вызывают резонансные колебания осцилляторов качения. Рабочий орган раскачивает и синхронизирует осцилляторы ИЭ на резонансной частоте ω1 = ω – ω2 ≈ λ1 = νω.
Заключение
Анализ показывает, что с помощью легких маятников (ε << 1) удается раскачать массивный рабочий орган машины, существенно снизить энергопотребление, повысить стабильность резонансного режима колебаний при высокой добротности колебательной системы. При этом реализуется самоуправляемое и самоподдерживаемое собственное движение машины за счет слабых, но «умных» воздействий.
Таким образом, применение параметрических (резонансных) вибровозбудителей обеспечивает высокие количественные и качественные показатели, которыми не обладают машины, построенные на иных принципах.
Рецензенты:
Панов А.Ю., д.т.н., заведующий кафедрой «Теоретическая и прикладная механика», ФГБОУ ВПО «Нижегородский государственный технический университет им. Р.Е. Алексеева», г. Нижний Новгород;
Кабалдин Ю.Г., д.т.н., кафедра «Технология и оборудование машиностроения», ФГБОУ ВПО «Нижегородский государственный технический университет им. Р.Е. Алексеева», г. Нижний Новгород.
Работа поступила в редакцию 02.06.2014.
Библиографическая ссылка
Антипов В.И., Денцов Н.Н., Кошелев А.В. ДИНАМИКА ПАРАМЕТРИЧЕСКИ ВОЗБУЖДАЕМОЙ ВИБРАЦИОННОЙ МАШИНЫ С ИЗОТРОПНОЙ УПРУГОЙ СИСТЕМОЙ // Фундаментальные исследования. 2014. № 8-5. С. 1037-1042;URL: https://fundamental-research.ru/ru/article/view?id=34713 (дата обращения: 30.03.2025).



